방정식과 부등식
람다 $\lambda$의 차례
복소수와 그 연산
1. 복소수
(1) 허수단위 $i$
제곱하여 $-1$이 되는 수를 기호 $\bf{\it{i}}$ 와 같이 나타내고, 이것을 허수단위라 합니다. 즉 $$i = \sqrt{-1}, \:\: i^{2}=-1$$
(2) 복소수
실수 $a$, $b$에 대하여 $a+bi$ 꼴로 나타내는 수를 복소수라 하고, $a$를 이 복소수의 실수부분, $b$를 이 복소수의 허수부분이라고 합니다.
(3) 복소수의 종류
① 허수와 허수단위: 복소수 $a+bi$ ($a$, $b$는 실수)에서 실수가 아닌 복소수 $a+bi$ ($b \ne 0$)를 허수라고 하고, 특히 실수 부분이 $0$인 허수 $bi$ ($b \ne 0$)를 순허수라 합니다.
② 복소수는 다음과 같이 분류할 수 있습니다. ($a$, $b$는 실수)
$$\textbf{복소수 }a+bi \, \begin{cases} \textbf{실수 }a & (b = 0) \\ \\ \textbf{허수 }a+bi & (b \ne 0) \begin{cases} \textbf{순허수 }bi & (a=0,\: b \ne 0) \\ \\ \textbf{순허수가 아닌 허수 }a+bi & (a \ne 0,\: b \ne 0) \end{cases} \end{cases}$$
2. 복소수가 서로 같을 조건
두 복소수 $a+bi$, $c+di$ ($a$, $b$, $c$, $d$는 실수)에 대하여
① $a = c$, $b = d$이면 $a + bi = c + di$
$a + bi = c + di$이면 $a = c$, $b = d$
② $a = 0$, $b = 0$이면 $a + bi = 0$
$a + bi = 0$이면 $a = 0$, $b = 0$
3. 켤레복소수
복소수 $a + bi$ ($a$, $b$는 실수)에 대하여 허수부분의 부호를 바꾼 복소수 $a -\, bi$를 $a + bi$의 켤레복소수라 하고, 기호로 $\overline{a + bi}$ 와 같이 나타냅니다. 즉 $\overline{a + bi} = a -\, bi$입니다.
복소수 $z$와 그 켤레복소수 $\overline{z}$에 대하여
① $z$가 실수이면 $\overline{z} = z$
$\overline{z} = z$이면 $z$는 실수
② $z$가 순허수이면 $\overline{z} = -z$
$\overline{z} = -z$이고 $z \ne 0$이면 $z$는 순허수
4. 복소수의 사칙연산
(1) 복소수의 사칙연산
$a$, $b$, $c$, $d$가 실수일 때
① 덧셈: $(a + bi) + (c + di) = (a + c) + (b + d)i$
② 뺄셈: $(a + bi) -\, (c + di) = (a – c) + (b -\, d)i$
③ 곱셈: $(a + bi)(c + di) = (ac -\, bd) + (ad + bc)i$
④ 나눗셈: $\dfrac{a + bi}{c + di} = \dfrac{(a + bi)(c -\, di)}{(c + di)(c -\, di)}$
$= \dfrac{ac + bd}{c^2 + d^2} +\dfrac{bc -\, ad}{c^2 + d^2}i$
복소수 $z$, $w$, $u$에 대하여
① 교환법칙: $z + w = w + z$, $zw = wz$
② 결합법칙: $(z + w) + u = w + (z + u)$, $(zw)u = w(zu)$
③ 분배법칙: $z(w + u) = zw + zu$, $(z + w)u = zu + wu$
(2) 켤레복소수의 성질
복소수 $z_1$, $z_2$의 켤레복소수를 각각 $\overline{z_{1}}$, $\overline{z_{2}}$라 할 때
① $\overline{(\overline{z_1})} = z_1$
② $z_1 + \overline{z_1}$는 실수, $z_{1}\overline{z_1}$는 실수
③ $\overline{z_{1} + z_2} = \overline{z_{1}} + \overline{z_2}$, $\overline{z_{1} -\, z_2} = \overline{z_{1}} -\, \overline{z_2}$
④ $\overline{z_{1}z_2} = \overline{z_{1}} \times \overline{z_2}$, $\overline{\left(\dfrac{z_1}{z_2}\right)} = \dfrac{\overline{z_{1}}}{\overline{z_2}}$ (단, $z_{2} \ne 0$)
(3) $i$의 거듭제곱
$i^{n}$ ($n$은 자연수)의 값은 $i$, $-1$, $-i$, $1$ 이 이 순서대로 반복되어 나타나므로 다음과 같은 규칙을 갖습니다.
$i^{4k} = 1$, $i^{4k+1} = i$, $i^{4k+2} = -1$, $i^{4k+3} = -i$ (단, $k$는 자연수)
$i^{n}$ ($n$은 자연수)의 값은 $n$을 $4$로 나누었을 때의 나머지가 같으면 그 값은 같습니다.
이차방정식의 판별식
1. 이차방정식의 풀이
(1) 이차방정식의 실근과 허근
계수가 실수인 이차방정식은 복소수의 범위에서 항상 근을 갖습니다. 이때 실수인 근을 실근, 허수인 근을 허근이라 합니다.
(2) 이차방정식의 풀이
① 인수분해를 이용한 풀이
$x$에 대한 이차방정식 $(ax -\, b)(cx -\, d) = 0$의 근은 $$x=\frac{b}{a} \text{ 또는 }x=\frac{d}{c}$$
② 근의 공식을 이용한 풀이
계수가 실수인 이차방정식 $ax^2 + bx + c = 0$의 근은 $$x = \frac{-b \pm \sqrt{b^2 -\, 4ac}}{2a}$$
$x$의 계수가 짝수인 이차방정식 $ax^2 + 2b^{\prime}x + c = 0$의 근은 $$x = \frac{- b^{\prime} \pm \sqrt{{b^{\prime}}^{2} -\, ac}}{a}$$
2. 이차방정식의 근의 판별
(1) 계수가 실수인 이차방정식 $ax^2 + bx + c = 0$의 근 $x = \dfrac{-b \pm \sqrt{b^{2} -\, 4ac}}{2a}$가 실근인지 허근인지는 근호 안의 식 $b^{2} -\, 4ac$의 부호에 따라 판별할 수 있으므로 $b^{2} -\, 4ac$를 이 방정식의 판별식이라고 하고, 기호로 $D$로 나타냅니다. 즉 $D = b^{2} -\, 4ac$입니다.
$x$의 계수가 짝수인 이차방정식 $ax^2 + 2b^{\prime}x + c = 0$에서는 판별식 $D$ 대신 $\dfrac{D}{4} = {b^{\prime}}^{2} -\, ac$를 이용할 수 있습니다.
(2) 이차방정식의 근의 판별
계수가 실수인 이차방정식 $ax^2 + bx + c = 0$에서 $D = b^{2} -\, 4ac$라 할 때
① $D \gt 0$이면 서로 다른 두 실근
② $D = 0$이면 중근(서로 같은 두 실근)
③ $D \lt 0$이면 서로 다른 두 허근을 갖습니다.
이차방정식 $ax^2 + bx + c = 0$은 두 개의 근을 갖습니다.
이차방정식 $ax^2 + bx + c = 0$가 두 개의 실근을 갖으면 $D \ge 0$입니다.
이차방정식 $ax^2 + bx + c = 0$가 서로 다른 두 개의 실근을 갖으면 $D > 0$입니다.
이차방정식 $ax^2 + bx + c = 0$에서 $x^2$의 계수와 상수항의 부호가 다르면, 즉 $ac \lt 0$이면 $D = b^{2} -\, 4ac > 0$이므로 서로 다른 두 실근을 갖습니다.
이차방정식의 근과 계수와의 관계
1. 이차방정식의 근과 계수와의 관계
(1) 이차방정식 $ax^2 + bx + c = 0$의 두 근을 $\alpha$, $\beta$라 하면 ($D = b^{2} -\, 4ac$)$$\alpha + \beta = – \frac{b}{a}, \:\, \alpha\beta = \frac{c}{a}, \:\, \lvert \alpha -\, \beta \, \rvert = \frac{
\sqrt{D}}{| a |} $$
(2) 두 수를 근으로 하는 이차방정식
두 수 $\alpha$, $\beta$를 근으로 하고 $x^2$의 계수가 $1$인 이차방정식은 $$x^{2} -\, (\alpha + \beta)x + \alpha\beta = 0$$
2. 이차식의 인수분해
이차방정식 $ax^2 + bx + c = 0$의 두 근을 $\alpha$, $\beta$라 하면 $$ax^{2} + bx + c = a(x -\, \alpha)(x -\, \beta)$$
계수가 실수인 이차식은 복소수의 범위에서 항상 두 일차식의 곱으로 인수분해할 수 있습니다.
3. 이차방정식의 켤레근
이차방정식 $ax^{2} + bx + c = 0$에서
① $a$, $b$, $c$가 유리수일 때, $p + q\sqrt{m}$이 근이면 $p -\, q\sqrt{m}$도 근입니다.
(단, $p$, $q$는 유리수, $q \ne 0$이고 $\sqrt{m}$은 무리수)
② $a$, $b$, $c$가 실수일 때, $p + qi$가 근이면 $p -\, qi$도 근입니다.
(단, $p$, $q$는 실수, $q \ne 0$이고 $i$는 허수단위)
이차방정식과 이차함수의 관계
1. 이차방정식과 이차함수의 관계
(1) 이차방정식과 이차함수의 관계
이차함수 $y = ax^{2} + bx + c$의 그래프와 $x$축의 교점의 $x$좌표는 이차방정식 $ax^{2} + bx + c = 0$의 실근입니다.
이차함수 $y = ax^{2} + bx + c$의 그래프와 $x$축은 이차방정식 $ax^{2} + bx + c = 0$의 판별식 $D$의 부호가 $D \gt 0$일 때 두 개의 점에서 만나고 $D = 0$일 때 한 점에서 만납니다. 한 점에서 만날 때 접한다고 합니다.
(2) 이차함수의 그래프와 이차방정식의 해
이차함수 $y = ax^{2} + bx + c$의 그래프와 이차방정식 $ax^{2} + bx + c = 0$의 해 사이에는 이차방정식 $ax^{2} + bx + c = 0$의 판별식 $D$의 부호에 따라 다음과 같은 관계가 성립합니다.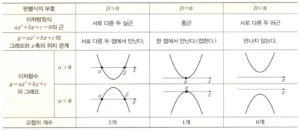
2. 이차함수의 그래프와 직선의 위치 관계
이차함수 $y = ax^2 + bx + c$의 그래프와 직선 $y = mx + n$의 교점의 $x$좌표는 이차방정식 $ax^2 + bx + c = mx + n$, 즉 $ax^2 + (b -\, m)x + c -\, n = 0$의 실근입니다. 따라서 이차함수의 그래프와 직선의 위치 관계는 이차방정식 $ax^2 + (b -\, m)x + c -\, n = 0$의 판별식 $D = (b -\, m)^{2} -\, 4a(c -\, n)$의 부호에 의해 다음과 같습니다.
① $D > 0$: 서로 다른 두 점에서 만납니다.
② $D = 0$: 한 점에서 만납니다. 접한다고 합니다.
③ $D < 0$: 만나지 않습니다.
이차함수의 최대 최소
1. 실수 전체 범위에서의 최대, 최소
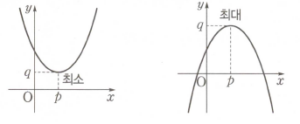
$x$의 값의 범위가 실수 전체일 때, 이차함수 $y = a(x -\, p)^2 + q$의 최댓값과 최솟값은 $a$의 부호에 따라 다음과 같습니다.
① $a \gt 0$일 때
$x = p$에서 최솟값 $q$를 갖고, 최댓값은 없습니다.
② $a \lt 0$일 때
$x = p$에서 최댓값 $q$를 갖고, 최솟값은 없습니다.
위의 사실은 다음과 일치합니다.
$x$의 값의 범위가 실수 전체일 때, 이차함수 $f(x) = ax^2 + bx + c$의 최댓값과 최솟값은 $a$의 부호에 따라 다음과 같습니다.
① $a \gt 0$일 때
$x = – \dfrac{b}{2a}$에서 최솟값 $f\left( – \dfrac{b}{2a} \right)$를 갖고, 최댓값은 없습니다.
② $a \lt 0$일 때
$x = – \dfrac{b}{2a}$에서 최댓값 $f\left( – \dfrac{b}{2a} \right)$를 갖고, 최솟값은 없습니다.
 이차함수 $y = ax^2 + bx + c$의 최댓값과 최솟값은 이차함수의 식을 $y = a(x -\, p)^2 + q$의 꼴로 변형하여 구해도 되지만 $p = – \frac{b}{2a}$이므로 $f(x) = ax^2 + bx + c$라 할 때 함숫값 $f(- \frac{b}{2a})$ 만 구하면 충분합니다. 즉 $q = f(p)$입니다.
이차함수 $y = ax^2 + bx + c$의 최댓값과 최솟값은 이차함수의 식을 $y = a(x -\, p)^2 + q$의 꼴로 변형하여 구해도 되지만 $p = – \frac{b}{2a}$이므로 $f(x) = ax^2 + bx + c$라 할 때 함숫값 $f(- \frac{b}{2a})$ 만 구하면 충분합니다. 즉 $q = f(p)$입니다.
2. 제한된 범위에서의 이차함수의 최대, 최소
$x$의 값의 범위가 $\alpha \le x \le \beta$일 때, 이차함수 $f(x) = ax^2 = bx + c$의 최댓값과 최솟값은 $y = f(x)$의 그래프의 꼭짓점의 $x$좌표인 $p = -\frac{b}{2a}$의 값에 따라 다음과 같습니다.
① $p$가 $\alpha \le x \le \beta$에 속할 때, 즉 $\alpha \le p \le \beta$이면
$f(p)$, $f(\alpha)$, $f(\beta)$ 중 가장 큰 값이 최댓값, 가장 작은 값이 최솟값입니다.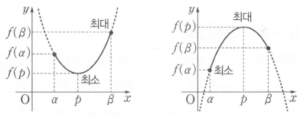
② $p$가 $\alpha \le x \le \beta$에 속하지 않을 때, 즉 $p \lt \alpha$ 또는 $p \gt \beta$이면
$f(\alpha)$, $f(\beta)$ 중 가장 큰 값이 최댓값, 가장 작은 값이 최솟값입니다. 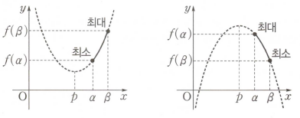
삼차방정식과 사차방정식
1. 삼차방정식과 사차방정식
(1) 삼차방정식과 사차방정식
다항식 $P(x)$가 $x$에 대한 삼차식, 사차식인 경우 방정식 $P(x) = 0$을 각각 $x$에 대한 삼차방정식, 사차방정식이라 합니다. 이때 방정식 $P(x) = 0$은 좌변 $P(x)$를 인수분해한 후 다음을 이용하여 방정식을 풉니다.
① $ABC = 0$이면 $A = 0$ 또는 $B = 0$ 또는 $C = 0$
② $ABCD = 0$이면 $A = 0$ 또는 $B = 0$ 또는 $C = 0$ 또는 $D = 0$
(2) 삼차, 사차방정식 $P(x) = 0$의 풀이
① 인수정리를 이용: 다항식 $P(x)$에 대하여 $P(\alpha) = 0$이면 $P(x) = (x -\, \alpha)Q(x)$임을 이용하여 $P(x)$을 인수분해한 후 방정식을 풉니다.
② 치환을 이용: 방정식에 공통부분이 있으면 공통부분을 한 문자로 치환하여 그 문자에 대한 방정식으로 변형한 후 인수분해하여 풉니다.
(3) 특수한 형태의 사차방정식의 풀이
① $x^4 + ax^2 + b = 0$ 꼴: $x^2 = X$로 치환하거나 $ax^2$를 적당히 분리하여 $(x^2 + c)^2 -\, (dx)^2$ 꼴로 변형한 후 인수분해하여 풉니다.
② $ax^4 + bx^3 + cx^2 + bx + a = 0$ 꼴: 양변을 $x^2$으로 나눈 후 $x + \dfrac{1}{x} = X$로 치환하여 $X$에 대한 이차방정식을 풉니다.
2. 삼차방정식의 근과 계수와의 관계
(1) 삼차방정식의 근과 계수와의 관계
삼차방정식 $ax^3 + bx^2 + cx + d = 0$의 세근을 $\alpha$, $\beta$, $\gamma$라 하면
$$\alpha + \beta + \gamma = -\frac{b}{a}, \:\,\alpha\beta + \beta\gamma + \gamma\alpha = \frac{c}{a}, \:\,\alpha\beta\gamma = -\frac{d}{a}$$
(2) 세 수를 근으로 하는 삼차방정식
세 수 $\alpha$, $\beta$, $\gamma$를 근으로 하고 $x^3$의 계수가 $1$인 삼차방정식은 $$x^3 -\, (\alpha + \beta + \gamma)x^2 + (\alpha\beta + \beta\gamma + \gamma\alpha)x -\, \alpha\beta\gamma = 0$$
3. 삼차방정식의 켤레근
삼차방정식 $ax^{3} + bx^2 + cx + d = 0$에서
① $a$, $b$, $c$, $d$가 유리수일 때, $p + q\sqrt{m}$이 근이면 $p -\, q\sqrt{m}$도 근입니다.
(단, $p$, $q$는 유리수, $q \ne 0$이고 $\sqrt{m}$은 무리수)
② $a$, $b$, $c$, $d$가 실수일 때, $p + qi$가 근이면 $p -\, qi$도 근입니다.
(단, $p$, $q$는 실수, $q \ne 0$이고 $i$는 허수단위)
4. 방정식 $x^3 = 1$의 허근의 성질
방정식 $x^3 – 1 = 0$의 한 허근을 $\omega$라 하면 다음 성질이 성립합니다.
① $\omega^{3} = 1$, $\omega^{2} + \omega + 1 = 0$
② $\omega + \overline{\omega} = -1$, $\omega\overline{\omega} = 1$
③ $\omega^{2} = \dfrac{1}{\omega} = \overline{\omega}$
방정식 $x^3 = 1$, 즉 $x^3 -\, 1 = 0$에서 $(x -\, 1)(x^2 + x + 1) = 0$이므로 이차방정식 $x^2 + x + 1 = 0$의 두 허근은 $\omega$ 와 $\overline{\omega}$ 입니다. 삼차방정식 $x^3 = 1$의 두 허근이기도 합니다.
연립이차방정식
1. 연립이차방정식
(1) 미지수가 $2$개인 연립이차방정식
미지수가 $2$개인 연립이차방정식에서 차수가 가장 높은 방정식이 이차방정식일 때 이 연립방정식을 미지수가 $2$개인 연립이차방정식이라고 합니다.
(2) 연립이차방정식의 풀이
① 일차방정식과 이차방정식으로 이루어진 연립이차방정식
일차방정식을 한 미지수에 대하여 정리한 것을 이차방정식에 대입하여 미지수가 $1$개인 이차방정식으로 만들어 풉니다.
② 두 개의 이차방정식으로 이루어진 연립이차방정식
한 이차방정식에서 이차식을 두 일차식의 곱으로 인수분해한 후 일차방정식과 이차방정식으로 이루어진 연립이차방정식으로 만들어 풉니다.
③ $x$, $y$에 대한 대칭식으로 이루어진 연립이차방정식
$x + y = u$, $xy = v$로 놓고 $u$, $v$에 대한 연립방정식으로 변형하여 방정식을 푼 후 $x$, $y$는 $t$에 대한 이차방정식 $t^{2} -\, ut + v = 0$의 두 근임을 이용해서 풉니다.
여러 가지 일차부등식
1. 부등식의 기본 성질
실수 $a$, $b$, $c$에 대하여
① $a \gt b$, $b \gt c$ 이면 $a \gt c$
② $a \gt b$ 이면 $a + c \gt b + c$, $a -\, c \gt b -\, c$
③ $a \gt b$, $c \gt 0$ 이면 $ac \gt bc$, $\dfrac{a}{c} \gt \dfrac{b}{c}$
④ $a \gt b$, $c \lt 0$ 이면 $ac \lt bc$, $\dfrac{a}{c} \lt \dfrac{b}{c}$
2. 부등식 $ax \gt b$의 풀이
부등식 $ax \gt b$의 해는
① $a \gt 0$일 때, $x \gt \dfrac{b}{a}$
② $a \lt 0$일 때, $x \lt \dfrac{b}{a}$
③ $a = 0$일 때, $\begin{cases} b \ge 0 \, \textbf{이면 해는 없습니다.} \\ b \lt 0 \, \textbf{이면 해는 모든 실수입니다.} \end{cases}$
3. 연립일차부등식
(1) 연립부등식: 두 개 이상의 부등식을 한 쌍으로 묶어서 나타낸 것입니다.
(2) 연립일차부등식: 일차부등식으로만 이루어진 연립부등식입니다.
(3) 연립부등식의 해: 연립부등식에서 각 부등식의 공통인 해를 연립부등식의 해라 하고 연립부등식의 해를 구하는 것을 연립부등식을 푼다고 합니다.
(4) 연립일차부등식의 풀이
① 각 일차부등식을 풉니다.
② 각 부등식의 해를 수직선 위에 나타냅니다.
③ 공통부분을 찾아 주어진 연립부등식의 해를 구합니다.
4. 특수한 해를 갖는 연립일차부등식
(1) 해가 한 개인 경우: 연립부등식에서 각 부등식의 해를 수직선 위에 나타내었을 때, 공통부분이 $a$ 뿐이면 연립부등식의 해는 $x = a$입니다.
즉, $\begin{cases} x \le a \\ x \ge a \end{cases}\,$이면 해는 $x = a$입니다.
(2) 해가 없는 경우: 연립부등식에서 각 부등식의 해를 수직선 위에 나타내었을 때, 공통부분이 없으면 연립부등식의 해는 없습니다.
① $\begin{cases} x \le a \\ x \ge b \end{cases}$ ($a \lt b$)는 해가 없습니다.
② $\begin{cases} x \lt a \\ x \ge a \end{cases}\,$는 해가 없습니다.
③ $\begin{cases} x \lt a \\ x \gt a \end{cases}\,$는 해가 없습니다.
5. $A \lt B \lt C$ 꼴의 부등식
$A \lt B \lt C$ 꼴의 부등식은 두 부등식 $A \lt B\,$와 $B \lt C$를 하나로 나타낸 것이므로 연립부등식 $\begin{cases} A \lt B \\ B \lt C \end{cases}$ 꼴로 고쳐서 풉니다.
6. 절댓값 기호를 포함한 부등식
(1) $a \gt 0$일 때
① $|\,x\,| \lt a$의 해는 $-a \lt x \lt a$
② $|\,x\,| \gt a$의 해는 $x \lt -a$ 또는 $x \gt a$
(2) 절댓값 기호를 포함한 부등식의 풀이
① 절댓값 기호 안의 식의 값이 $0$이 되는 $x$의 값을 기준으로 $x$의 범위를 나눕니다.
② 각 범위에서 절댓값 기호를 없앤 후 식을 정리하여 해를 구합니다.
이때 $|\,x -\, a\,| = \begin{cases} \: x -\, a & (x \ge a) \\ -(x -\, a) & (x \lt a) \end{cases}$ 임을 이용합니다.
③ 위에서 구한 해를 합친 $x$의 범위를 구합니다.
이차부등식과 연립이차부등식
1. 이차부등식과 이차함수의 관계
(1) 이차부등식
부등식의 모든 항을 좌변으로 이항하여 정리했을 때, 좌변이 $x$에 대한 이차식인 부등식입니다.
(2) 이차부등식의 해와 이차함수의 그래프
① $ax^2 + bx + c \gt 0$의 해
$y = ax^2 + bx + c$에서 $y \gt 0$인 $x$의 범위
$y = ax^2 + bx + c$의 그래프에서 $x$축보다 위쪽에 있는 부분의 $x$의 값의 범위
② $ax^2 + bx + c \lt 0$의 해
$y = ax^2 + bx + c$에서 $y \lt 0$인 $x$의 범위
$y = ax^2 + bx + c$의 그래프에서 $x$축보다 아래쪽에 있는 부분의 $x$의 값의 범위
2. 이차부등식의 풀이
이차방정식 $ax^2 + bx + c = 0\,$ ($a \gt 0$)의 판별식을 $D$라 하고, 이차함수 $y = ax^2 + bx + c$ ($a \gt 0$)의 그래프가 $D \ge 0$일 때 $x$축과 만나는 점의 $x$좌표를 $\alpha$, $\beta\,$ ($\alpha \le \beta$)라고 하면 이차부등식의 해는 다음과 같습니다. ($a \gt 0$)
(1) $D \gt 0$인 경우 ($\alpha \lt \beta$)
① $ax^2 + bx + c \gt 0$의 해는 $x \lt \alpha$ 또는 $x \gt \beta$
② $ax^2 + bx + c \ge 0$의 해는 $x \le \alpha$ 또는 $x \ge \beta$
③ $ax^2 + bx + c \lt 0$의 해는 $\alpha \lt x \lt \beta$
④ $ax^2 + bx + c \le 0$의 해는 $\alpha \le x \le \beta$
(2) $D = 0$인 경우
① $ax^2 + bx + c \gt 0$의 해는 $x \ne \alpha$인 모든 실수
② $ax^2 + bx + c \ge 0$의 해는 모든 실수
③ $ax^2 + bx + c \lt 0$의 해는 없습니다.
④ $ax^2 + bx + c \le 0$의 해는 $x = \alpha$
(3) $D \lt 0$인 경우
① $ax^2 + bx + c \gt 0$의 해는 모든 실수
② $ax^2 + bx + c \ge 0$의 해는 모든 실수
③ $ax^2 + bx + c \lt 0$의 해는 없습니다.
④ $ax^2 + bx + c \le 0$의 해는 없습니다.
3. 이차부등식의 작성
(1) 해가 $\alpha \lt x \lt \beta$이고 $x^2$의 계수가 $1$인 이차부등식은
$(x -\, \alpha)(x -\, \beta) \lt 0$, $\,$ 즉 $x^2 -\, (\alpha + \beta)x + \alpha\beta \lt 0$
(2) 해가 $x \lt \alpha$ 또는 $x \gt \beta$ ($\alpha \lt \beta$)이고 $x^2$의 계수가 $1$인 이차부등식은
$(x -\, \alpha)(x -\, \beta) \gt 0$, $\,$ 즉 $x^2 -\, (\alpha + \beta)x + \alpha\beta \gt 0$
4. 이차부등식이 항상 성립하기 위한 조건
(1) 모든 실수 $x$에 대하여 이차부등식 $ax^2 + bx + c \gt 0$이 성립하려면 $$a \gt 0, \:\, D \lt 0$$
(2) 모든 실수 $x$에 대하여 이차부등식 $ax^2 + bx + c \ge 0$이 성립하려면 $$a \gt 0, \:\, D \le 0$$
(3) 모든 실수 $x$에 대하여 이차부등식 $ax^2 + bx + c \lt 0$이 성립하려면 $$a \lt 0, \:\, D \lt 0$$
(4) 모든 실수 $x$에 대하여 이차부등식 $ax^2 + bx + c \le 0$이 성립하려면 $$a \lt 0, \:\, D \le 0$$
(단, $D$는 이차방정식 $ax^2 + bx + c = 0$의 판별식. 즉, $D = b^2 -\,4ac$)
5. 연립이차부등식
(1) 연립이차부등식
차수가 가장 높은 부등식이 이차부등식인 연립부등식입니다.
(2) 연립이차부등식의 풀이
각 부등식의 해를 구한 다음 공통부분을 찾아 주어진 연립부등식의 해를 구합니다.
6. 이차방정식의 실근의 조건
(1) 이차방정식의 실근의 부호
계수가 실수인 이차방정식을 $ax^2 + bx + c = 0$라 하면
① 두 근이 모두 양수인 경우: $$D \ge 0, \:\, -\frac{b}{a} \gt 0, \:\, \frac{c}{a} \gt 0$$
② 두 근이 모두 음수인 경우: $$D \ge 0, \:\, -\frac{b}{a} \lt 0, \:\, \frac{c}{a} \gt 0$$
③ 두 근의 부호가 반대인 경우: $$\frac{c}{a} \lt 0, \text{ 즉 }ac \lt 0$$
이차방정식 $ax^2 + bx + c = 0$의 두 실근을 $\alpha$, $\beta$라 하면 근과 계수와의 관계에 의해 $\alpha + \beta = -\frac{b}{a}$, $\alpha\beta = \frac{c}{a}$입니다.
(2) 이차방정식의 근의 분리
이차방정식 $ax^2 + bx + c = 0$ ($a \gt 0$)의 판별식을 $D$라 하고, $f(x) = ax^2 + bx + c$라 하면
① 두 근이 모두 $q$ 보다 큰 경우: $$D \ge 0, \:\, f(q) \gt 0, \:\, -\frac{b}{2a} \gt q$$
② 두 근이 모두 $q$ 보다 작은 경우: $$D \ge 0, \:\, f(q) \gt 0, \:\, -\frac{b}{2a} \lt q$$
③ 두 근 사이에 $q$가 있는 경우: $$f(q) \lt 0$$
④ 두 근이 $q$, $\,r$ ($q \lt r$) 사이에 있는 경우: $$D \ge 0, \:\, f(q) \gt 0, \:\, f(r) \gt 0, \:\, q \lt -\frac{b}{2a} \lt r$$
$q = 0$일 때의 ①, ②, ③은 (1)의 ①, ②, ③과 각각 일치합니다.
여러 가지 방정식과 부등식
1. 절댓값 기호를 포함한 방정식과 부등식
(1) $a \gt 0$일 때
① $|\,f(x)\,| = a$의 해는 $f(x) = -a$ 또는 $f(x) = a$을 풀어서 구합니다.
② $|\,f(x)\,| \lt a$의 해는 $-a \lt f(x) \lt a$을 풀어서 구합니다.
③ $|\,f(x)\,| \gt a$의 해는 $f(x) \lt -a$ 또는 $f(x) \gt a$을 풀어서 구합니다.
(2) 절댓값 기호를 포함한 방정식 부등식의 풀이
① 절댓값 기호 안의 식의 값이 $0$이 되는 $x$의 값을 기준으로 $x$의 범위를 나눕니다.
② 각 범위에서 절댓값 기호를 없앤 후 식을 정리하여 해를 구합니다.
이때 $|\,f(x)\,| = \begin{cases} \: f(x) & (f(x) \ge 0\textbf{인 }x\textbf{의 범위}) \\ -f(x) & (f(x) \lt 0\textbf{인 }x\textbf{의 범위}) \end{cases}$ 임을 이용합니다.
③ 위에서 구한 해를 합친 $x$의 값 또는 범위를 구합니다.