23년 11월 고2 교육청
6. 함수 $$f(x) = \begin{cases} ax^{2}+bx+1 & (x \lt 1) \\ -3bx-1 & (x \ge 1) \end{cases}$$ 이 실수 전체의 집합에서 미분가능할 때, $a+b$의 값은? (단, $a$, $b$는 상수이다.) [3점]
① $-3$
② $-1$
③ $1$
④ $3$
⑤ $5$
③
함수 $f(x)$가 실수 전체의 집합에서 미분가능하므로
함수 $f(x)$는 $x = 1$에서 미분가능하다.
그러므로 함수 $f(x)$는 $x=1$에서 연속이다.
$\displaystyle \lim_{x \to 1-}f(x) = \lim_{x \to 1+}f(x) = f(1)$에서
$a+b+1 = -3b-1$
$a = -4b-2$
$\begin{align}\displaystyle \lim_{x \to 1-}\frac{f(x)-f(1)}{x-1} &= \lim_{x \to 1-}\frac{(ax^{2}+bx+1)-(-3b-1)}{x-1} \\
&= \lim_{x \to 1-}\frac{ax^{2}+bx+3b+2)}{x-1} \\
&= \lim_{x \to 1-}\frac{(-4b-2)x^{2}+bx+3b+2)}{x-1} \\
&= \lim_{x \to 1-}\frac{(x-1)\{(-4b-2)x-3b-2)\}}{x-1} \\ &= -7b-4 \end{align}$
$\begin{align}\displaystyle \lim_{x \to 1+}\frac{f(x)-f(1)}{x-1} &= \lim_{x \to 1+}\frac{(-3bx-1)-(-3b-1)}{x-1} \\
&= \lim_{x \to 1+}\frac{ax^{2}+bx+3b+2)}{x-1} \\
&= \lim_{x \to 1-}\frac{-3b(x-1)}{x-1} \\ &= -3b \end{align}$
함수 $f(x)$가 $x=1$에서 미분가능하므로
$-7b-4 = -3b$에서 $b = -1$, $a=2$
따라서 $a+b = 1$
7. 함수 $f(x)$에 대하여 $f'(x) = 3x^{2}-6x$이고 $f(1) = 1$일 때, 함수 $f(x)$의 극솟값은? [3점]
① $-2$
② $-1$
③ $0$
④ $1$
⑤ $2$
8. 곡선 $y = \dfrac{1}{16}\times \left( \dfrac{1}{2} \right)^{x-m}$이 곡선 $y = 2^{x}+1$과 제$1$사분면에서 만나도록 하는 자연수 $m$의 최솟값은? [3점]
① $2$
② $4$
③ $6$
④ $8$
⑤ $10$
③
함수 $y = \frac{1}{16}\times \left( \frac{1}{2} \right)^{x-m}$은 $x$의 값이 증가하면 $y$의 값이 감소하고 함수 $y = 2^{x}+1$은 $x$의 값이 증가하면 $y$의 값도 증가한다.
곡선 $y = 2^{x}+1$은 점 $(0, 2)$를 지나므로 곡선 $y = \frac{1}{16}\times \left( \frac{1}{2} \right)^{x-m}$이 곡선 $y = 2^{x}+1$과 제$1$사분면에서 만나기 위해서는 곡선 $y = \frac{1}{16}\times \left( \frac{1}{2} \right)^{x-m}$이 $y$축과 만나는 점의 $y$좌표가 $2$보다 커야 한다.
$\frac{1}{16}\times \left( \frac{1}{2} \right)^{0-m} \gt 2$에서 $2^{m-4} \gt 2$, $m \gt 5$
따라서 자연수 $m$의 최솟값은 $6$
9. $2 \sin (\frac{\pi}{2}-\theta) = \sin \theta \times \tan (\pi+\theta)$일 때, $\sin^{2} \theta$의 값은? [3점]
① $\frac{1}{3}$
② $\frac{4}{9}$
③ $\frac{5}{9}$
④ $\frac{2}{3}$
⑤ $\frac{7}{9}$
④
$\sin (\frac{\pi}{2}-\theta) = \cos \theta$, $\tan (\pi+\theta) = \tan \theta$이므로
$2 \sin (\frac{\pi}{2}-\theta) = \sin \theta \times \tan (\pi+\theta)$에서
$2 \cos \theta = \sin \theta \times \tan \theta$
$2 \cos \theta = \sin \theta \times \frac{\sin \theta}{\cos \theta}$
$2 \cos^{2} \theta = \sin^{2} \theta$
$\sin^{2} \theta + \cos^{2} \theta = 1$이므로 $2(1-\sin^{2} \theta) = \sin^{2} \theta$
따라서 $\sin^{2} \theta = \dfrac{2}{3}$
10. 함수 $f(x)$가 모든 실수 $x$에 대하여 $$f(x) = x + \int_{0}^{2}f(t) dt$$ 를 만족시킬 때, $f(3)$의 값은? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
11. $a_{3} = 6$이고 공비가 양수인 등비수열 $\{ a_n \}$에 대하여 $a_{4}+a_{5} = 2(a_{6}+a_{7}) + 3(a_{8}+a_{9})$일 때, $a_1$의 값은? [3점]
① $10$
② $12$
③ $14$
④ $16$
⑤ $18$
⑤
등비수열 $\{ a_n \}$의 공비를 $r$ ($r \gt 0$)이라 하자.
$a_{4}+a_{5} = 2(a_{6}+a_{7}) + 3(a_{8}+a_{9})$에서
$a_{1}r^{3}+a_{1}r^{4} = 2(a_{1}r^{5}+a_{1}r^{6}) + 3(a_{1}r^{7}+a_{1}r^{8})$
$a_{1}r^{3}(1+r) = 2a_{1}r^{5}(1+r)+ 3a_{1}r^{7}(1+r)$
$3r^{4}+2r^{2}-1 = 0$, $(3r^{2}-1)(r^{2}+1) = 0$
$3r^{2}-1 = 0$에서 $r^{2} = \frac{1}{3}$
$a_{3} = a_{1}r^{2}$이므로 $6 = a_{1}\times \frac{1}{3}$
따라서 $a_{1} = 18$
12. 다항함수 $f(x)$에 대하여 함수 $g(x)$를 $$g(x) = (x^{2}-2x)f(x)$$ 라 하자. $g'(0)+g'(2) = 16$일 때, $f(2)-f(0)$의 값은? [3점]
① $6$
② $8$
③ $10$
④ $12$
⑤ $14$
13. 두 수열 $\{ a_n \}$, $\{ b_n \}$이 모든 자연수 $n$에 대하여 $a_{n}+b_{n} = n$을 만족시킨다. $\displaystyle \sum_{k =1}^{10}(3a_{k}+1) = 40$일 때, $\displaystyle \sum_{k =1}^{10}b_{k}$의 값은? [3점]
① $30$
② $35$
③ $40$
④ $45$
⑤ $50$
④
$\displaystyle \sum_{k =1}^{10}(3a_{k}+1) = 3\sum_{k =1}^{10}a_{k} + 10 = 40$에서 $\displaystyle \sum_{k =1}^{10}a_{k} = 10$
$\displaystyle \sum_{k =1}^{10}b_{k}$
$= \displaystyle \sum_{k =1}^{10}\{(a_{k}+b_{k})-a_{k}\}$
$= \displaystyle \sum_{k =1}^{10}k-\sum_{k =1}^{10}a_{k}$
$= \frac{10 \times 11}{2}-10$ $= 45$
14. 자연수 $n$ ($n \ge 2$)에 대하여 $m-2n$의 $n$제곱근 중에서 실수인 것의 개수를 $f(n)$이라 할 때, $f(2)+f(3)+f(4) = 3$을 만족시키는 모든 자연수 $m$의 값의 합은? [4점]
① $18$
② $23$
③ $28$
④ $33$
⑤ $38$
①
$m-6$의 세제곱근 중에서 실수인 것의 개수는 $m$의 값에 관계없이 $1$이므로 $f(3) = 1$
$f(2)+f(3)+f(4) = 3$에서 $f(2)+f(4) = 2$
$m-4$의 제곱근 중에서 실수인 것의 개수는
$m \gt 4$이면 $2$, $m=4$이면 $1$, $m \lt 4$이면 $0$이다.
$m-8$의 네제곱근 중에서 실수인 것의 개수는
$m \gt 8$이면 $2$, $m = 8$이면 $1$, $m \lt 8$이면 $0$이다.
$f(2) = 0$ 또는 $f(2) = 1$이면 $f(4) = 0$이므로
$f(2)+f(4) = 2$이기 위해서는 $f(2) = 2$, $f(4) = 0$이어야 한다.
그러므로 $4 \lt m \lt 8$
따라서 구하는 모든 자연수 $m$의 값의 합은
$5+6+7 = 18$
15. 수열 $\{ a_n \}$의 첫째항부터 제$n$항까지의 합을 $S_n$이라 할 때, 두 수열 $\{ a_n \}$, $\{ S_n \}$과 상수 $k$가 다음 조건을 만족시킨다.
모든 자연수 $n$에 대하여 $a_{n} + S_{n} = k$이다.
$s_{6} = 189$일 때, $k$의 값은? [4점]
① $192$
② $196$
③ $200$
④ $204$
⑤ $208$
①
$n = 1$일 때, $a_{1}+S_{1} = 2a_{1} = k$에서 $a_{1} = \frac{k}{2}$
$n \ge 2$일 때, $a_{n} = S_{n}-S_{n-1}$ $= (k-a_n)-(k-a_{n-1})$ $= -a_{n}+a_{n-1}$
이므로 $a_{n} = \frac{1}{2}a_{n-1}$ ($n \ge 2$)
수열 $\{ a_n \}$은 첫째항이 $\frac{k}{2}$이고 공비가 $\frac{1}{2}$인 등비수열이므로
$a_{6} = \frac{k}{2}\times (\frac{1}{2})^{5} = \frac{k}{64}$
$S_{6} = 189$이므로 $a_{6}+S_{6} = k$에서 $\frac{k}{64} + 189 = k$
따라서 $k = 192$
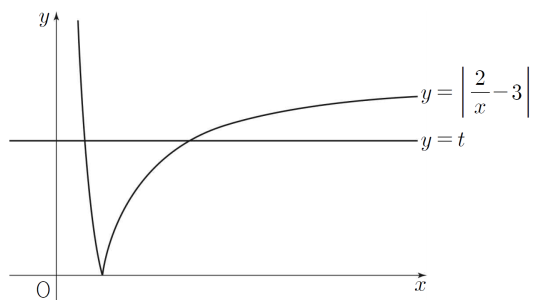
16. $0 \lt t \lt 3$인 실수 $t$에 대하여 함수 $y = \bigg\vert \,\dfrac{2}{x}-3\,\bigg\vert$의 그래프와 직선 $y = t$가 만나는 두 점 사이의 거리를 $f(t)$라 할 때, $\displaystyle \lim_{t \to 0+}\frac{f(t)}{t}$의 값은? [4점]
① $\frac{2}{9}$
② $\frac{1}{3}$
③ $\frac{4}{9}$
④ $\frac{5}{9}$
⑤ $\frac{2}{3}$
③
$x \lt 0$일 때, $| \frac{2}{x}-3 | = -\frac{2}{x}+3 \gt 3$이므로
$x \lt 0$에서 함수 $y = |\frac{2}{x}-3 |$의 그래프와 직선 $y=t$ ($0 \lt t \lt 3$)은 만나지 않는다.
$0 \lt x \lt \frac{2}{3}$일 때, $| \frac{2}{x}-3 | = \frac{2}{x}-3$
$\frac{2}{x}-3 = t$에서 $x = \frac{2}{3+t}$
$x \ge \frac{2}{3}$일 때, $| \frac{2}{x}-3 | = -\frac{2}{x}+3$
$-\frac{2}{x}+3 = t$에서 $x = \frac{2}{3-t}$
그러므로 $\displaystyle f(t) = \frac{2}{3-t}-\frac{2}{3+t} = \frac{4t}{(3-t)(3+t)}$
$\displaystyle \lim_{t \to 0+}\frac{f(t)}{t}$
$= \displaystyle \lim_{t \to 0+}\bigg\{ \frac{1}{t}\times \frac{4t}{(3-t)(3+t)} \bigg\}$
$= \displaystyle \lim_{t \to 0+}\frac{4}{(3-t)(3+t)}$ $= \dfrac{4}{9}$
17. $1$이 아닌 세 양수 $a$, $b$, $c$가 $$-4\log_{a}b = 54\log_{b}c = \log_{c}a$$ 를 만족시킨다. $b\times c$의 값이 $300$ 이하의 자연수가 되도록 하는 모든 자연수 $a$의 값의 합은? [4점]
① $91$
② $93$
③ $95$
④ $97$
⑤ $99$
⑤
$-4\log_{a}b = 54\log_{b}c = \log_{c}a = k$라 하면
$k^{3} = -4\log_{a}b \times 54\log_{b}c \times \log_{c}a$
$= -\dfrac{4 \log b}{\log a} \times \dfrac{54 \log c}{\log b} \times \dfrac{\log a}{\log c}$
$= -216$
에서 $k = -6$
$b = a^{-\frac{k}{4}} = a^{\frac{3}{2}}$, $c = a^{\frac{1}{k}} = a^{-\frac{1}{6}}$이므로
$b \times c = a^{\frac{3}{2}} \times a^{-\frac{1}{6}} = a^{\frac{4}{3}}$
$1$이 아닌 자연수 $a$에 대하여 $a^{\frac{4}{3}}$의 값이 자연수가 되기 위해서는 어떤 자연수 $n$ ($n \gt 1$)에 대하여
$a = n^{3}$이어야 한다.
$a^{\frac{4}{3}} = (n^{3})^{\frac{4}{3}} = n^{4} \le 300$
에서 가능한 자연수 $n$의 값은 $2$, $3$, $4$뿐이다.
따라서 구하는 모든 자연수 $a$의 값의 합은
$2^{3}+3^{3}+4^{3} = 8 + 27 + 64 = 99$
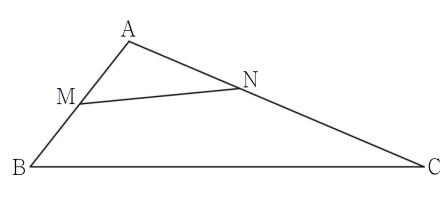
18. 그림과 같이 $2\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$인 삼각형 $\mathrm{ABC}$에 대하여 선분 $\mathrm{AB}$의 중점을 $\mathrm{M}$, 선분 $\mathrm{AC}$를 $3 : 5$로 내분하는 점을 $\mathrm{N}$이라 하자. $\overline{\mathrm{MN}} = \overline{\mathrm{AB}}$이고, 삼각형 $\mathrm{AMN}$의 외접원의 넓이가 $16\pi$일 때, 삼각형 $\mathrm{ABC}$의 넓이는? [4점]
① $24\sqrt{3}$
② $13\sqrt{13}$
③ $14\sqrt{14}$
④ $15\sqrt{15}$
⑤ $64$
④
$\overline{\mathrm{AB}} = k$라 하면 $2\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$에서 $\overline{\mathrm{AC}} = 2k$
점 $\mathrm{M}$은 선분 $\mathrm{AB}$의 중점이므로 $\overline{\mathrm{AM}} = \frac{k}{2}$
점 $\mathrm{N}$은 선분 $\mathrm{AC}$를 $3 : 5$로 내분하는 점이므로
$\overline{\mathrm{AN}} = 2k \times \frac{3}{8} = \frac{3}{4}k$
$2\overline{\mathrm{MN}} = \overline{\mathrm{AB}} = k$이므로 삼각형 $\mathrm{AMN}$에서 코사인법칙에 의하여
$\cos A = \dfrac{(\frac{k}{2})^{2}+(\frac{3}{4}k)^{2}-k^{2}}{2 \times \frac{k}{2} \times \frac{3}{4}k} = -\dfrac{1}{4}$
이므로 $\sin A = \sqrt{1-\cos^{2}A} = \frac{\sqrt{15}}{4}$
삼각형 $\mathrm{AMN}$의 외접원의 반지름의 길이를 $R$이라 하면
$\pi R^{2} = 16\pi$에서 $R = 4$
삼각형 $\mathrm{AMN}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{MN}}}{\sin A}= 2R$에서 $\dfrac{k}{\frac{\sqrt{15}}{4}} = 8$, $k = 2\sqrt{15}$
따라서 삼각형 $\mathrm{ABC}$의 넓이는
$\frac{1}{2} \times \overline{\mathrm{AB}} \times \overline{\mathrm{AC}} \times \sin A$
$= \frac{1}{2} \times 2\sqrt{15} \times 4\sqrt{15} \times \frac{\sqrt{15}}{4} = 15\sqrt{15}$
19. 실수 $k$에 대하여 함수 $f(x)$는 $f(x) = x^{3}-6x^{2}+9x+k$이다. 자연수 $n$에 대하여 직선 $y = 3n$과 함수 $y = f(x)$의 그래프가 만나는 점의 개수를 $a_n$이라 하자. $\displaystyle \sum_{n = 1}^{4}a_{n} = 7$을 만족시키는 모든 $k$의 값의 합은? [4점]
① $30$
② $33$
③ $36$
④ $39$
⑤ $42$
②
$f(x) = x^{3}-6x^{2}+9x+k$에서
$f'(x) = 3x^{2}-12x+9 = 3(x-1)(x-3)$
$f'(x) = 0$에서 $x = 1$ 또는 $x = 3$
함수 $f(x)$의 증가와 감소를 표로 나타내면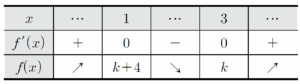
함수 $f(x)$는 $x=1$에서 극댓값 $k+4$, $x=3$에서 극솟값 $k$를 갖는다.
함수 $y = f(x)$
의 그래프는 그림과 같다.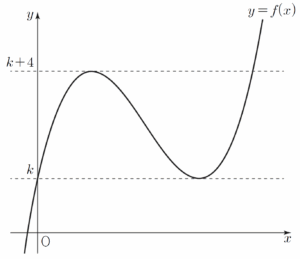 $a_n$은 직선 $y = 3n$과 함수 $y = f(x)$의 그래프가 만나는 점의 개수이므로
$a_n$은 직선 $y = 3n$과 함수 $y = f(x)$의 그래프가 만나는 점의 개수이므로
$a_{n} = \begin{cases} 1 & (3n \lt k \textbf{ 또는 } 3n \gt k+4) \\ 2 & (3n = k \textbf{ 또는 } 3n = k+4) \\ 3 & (k \lt 3n \lt k+4) \end{cases}$
어떠한 실수 $k$에 대해서도 $k = 3m$과 $k+4 = 3l$을 동시에 만족시키는 두 정수 $m$, $l$은 존재하지 않으므로 $a_{n} = 2$를 만족시키는 자연수 $n$의 개수는 $1$ 이하이다.
또한 가능한 $a_{n}$의 값은 $1$, $2$, $3$뿐이므로 $\displaystyle \sum_{n = 1}^{4}a_{n} = 7$이기 위해서는 네 수 $a_1$, $a_2$, $a_3$, $a_4$의 값 중 $1$은 $2$개, $2$는 $1$개, $3$은 $1$개이어야 한다.
그러므로 $a_{n} = 2$를 만족시키는 $n$의 개수는 $1$이다.
(ⅰ) $k$의 값이 $3$, $6$, $9$, $12$ 중 하나인 경우
$k = 3$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 2 + 3 + 1 + 1 = 7$
$k = 6$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 1 + 2 + 3 + 1 = 7$
$k = 9$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 1 + 1 + 2 + 3 = 7$
$k = 12$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 1 + 1 + 1 + 2 = 5 \ne 7$
(ⅱ) $k+4$의 값이 $3$, $6$, $9$, $12$ 중 하나인 경우
$k + 4 = 3$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 2 + 1 + 1 + 1 = 5 \ne 7$
$k + 4 = 6$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 3 + 2 + 1 + 1 = 7$
$k + 4 = 9$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 1 + 3 + 2 + 1 = 7$
$k + 4 = 12$일 때, $\displaystyle \sum_{n = 1}^{4}a_{n} = 1 + 1 + 3 + 2 = 7$
(ⅰ), (ⅱ)에 의하여 구하는 모든 실수 $k$의 값의 합은
$(3+6+9) + (2+5+8) = 33$
20. 함수 $f(x) = (x+1)(x-6)^{2}$과 양의 실수 $t$에 대하여 $g(t)$를 다음과 같이 정의한다.
두 점 $(0, 0)$, $(t, f(t))$를 지나는 직선의 기울기와 곡선 $y = f(x)$ 위의 점 $(k, f(k))$에서의 접선의 기울기가 같아지는 양의 실수 $k$의 개수가 $1$이면 $k$의 값을 $g(t)$,
$2$이면 $k$의 값 중 작은 값을 $g(t)$라 한다.
<보기>에서 옳은 것만을 있는 대로 고른 것은? [4점]
ㄱ. $f'(0) = 24$
ㄴ. $g(6) = \dfrac{4}{3}$
ㄷ. 함수 $g(t)$의 치역의 원소가 아닌 모든 자연수의 합은 $27$이다.
① ㄱ
② ㄴ
③ ㄱ, ㄴ
④ ㄱ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
⑤
ㄱ.
$f(x) = x^{3}-11x^{2}+24x+36$에서
$f'(x) = 3x^{2}-22x+24$이므로 $f'(0) = 24$ (참)
ㄴ.
두 점 $(0, 0)$, $(6, f(6))$을 지나는 직선의 기울기는 $\frac{f(6)}{6} = 0$
$f'(k) = \frac{f(6)}{6} = 0$에서
$3k^{2}-22k+24 = 0$, $(3k-4)(k-6) = 0$
$k = \frac{4}{3}$ 또는 $k = 6$
$\frac{4}{3}$와 $6$ 중 작은 값이 $\frac{4}{3}$이므로 $g(6) = \frac{4}{3}$ (참)
ㄷ.
함수 $f(x)$의 증가와 감소를 표로 나타내면 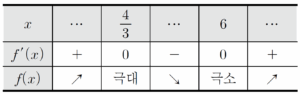
양의 실수 $t$에 대하여 두 점 $(0, 0)$, $(t, f(t))$를 지나는 직선의 기울기 $\frac{f(t)}{t}$는 $t=6$에서 최솟값 $0$을 갖는다.
또한 함수 $\frac{f(t)}{t}$는 양의 실수 전체의 집합에서 연속이고, $\displaystyle \lim_{t \to 0+}\frac{f(t)}{t} = \infty$이므로 $\{ \frac{f(t)}{t} \,|\, t \gt 0 \} = \{ y \,|\, y \ge 0 \}$이다.
한편 $f'(0) = 24$이므로
$\frac{f(t)}{t} \ge 24$이면 $f'(k) = \frac{f(t)}{t}$를 만족시키는 양의 실수 $k$의 개수는 $1$이고,
$0 \le \frac{f(t)}{t} \lt 24$이면 $f'(k) = \frac{f(t)}{t}$를 만족시키는 양의 실수 $k$의 개수는 $2$이다.
$\frac{f(t)}{t} = 24$에서 $t^{3}-11t^{2}+36 = 0$
$(t-2)(t^{2}-9t-18) = 0$
$t \gt 0$이므로 $t = 2$ 또는 $t = \frac{9+3\sqrt{17}}{2}$
이제 $\alpha = \frac{9+3\sqrt{17}}{2}$이라 하자.
$f'(x) = 24$에서
$3x^{2}-22x+24 = 24$, $3x(x-\frac{22}{3}) = 0$
$x = 0$ 또는 $x = \frac{22}{3}$
함수 $y = f(x)$의 그래프는 그림과 같다. 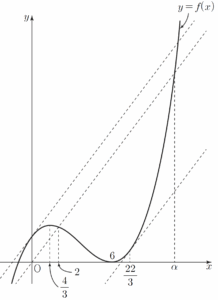 (ⅰ) $0 \lt t \le 2$ 또는 $t \ge \alpha$일 때
(ⅰ) $0 \lt t \le 2$ 또는 $t \ge \alpha$일 때
$\frac{f(t)}{t} \ge 24$이므로 $f'(k) = \frac{f(t)}{t}$를 만족시키는 양의 실수 $k$는 오직 $1$개 존재한다.
그 $k$의 값을 $k_1$이라 하면 $g(t) = k_{1}$이며 $k_{1} \ge \frac{22}{3}$이다.
그러므로 $\{ g(t) \,|\,0 \lt t \le 2 \text{ 또는 } t \ge \alpha \} \subset \{ k\,|\,k \ge \frac{22}{3} \}$ $\cdots\cdots$ ㉠
또한 $k \ge \frac{22}{3}$인 실수 $k$에 대하여 $f'(k) \ge 24$이며 $f'(k) = \frac{f(t)}{t}$인
두 양의 실수 $t_1$, $t_2$ ($0 \lt t_{1} \le 2$, $t_{2} \ge \alpha$)가 존재한다.
이때 $\frac{f(t_{1})}{t_1} = f'(x)$를 만족시키는 양의 실수 $x$의 값은 $k$뿐이므로 $g(t_1) = k$
그러므로 $\{ k\,|\,k \ge \frac{22}{3} \} \subset \{ g(t) \,|\,0 \lt t \le 2 \text{ 또는 } t \ge \alpha \}$ $\cdots\cdots$ ㉡
㉠, ㉡에 의하여 $\{ k\,|\,k \ge \frac{22}{3} \} = \{ g(t) \,|\,0 \lt t \le 2 \text{ 또는 } t \ge \alpha \}$
(ⅱ) $2 \lt t \lt 6$ 또는 $6 \lt t \lt \alpha$일 때
$0 \lt \frac{f(t)}{t} \lt 24$이므로 $f'(k) = \frac{f(t)}{t}$를 만족시키는 양의 실수 $k$가 $2$개 존재한다.
그 $k$의 값을 $k_2$, $k_3$ ($k_2 \lt k_3$)이라 하면
$g(t) = k_2$이며 $0 \lt k_{2} \lt \frac{4}{3}$이다.
그러므로 $\{ g(t) \,|\,2 \lt t \lt 6 \text{ 또는 } 6 \lt t \lt \alpha \} \subset \{ k\,|\,0 \lt k \lt \frac{4}{3} \}$ $\cdots\cdots$ ㉢
또한 $0 \lt k \lt \frac{4}{3}$인 실수 $k$에 대하여
$0 \lt f'(k) \lt 24$이며 $f'(k) = \frac{f(t)}{t}$인 두 양의 실수 $t_3$, $t_4$ ($2 \lt t_{3} \lt 6 \lt t_{4} \lt \alpha$)가존재한다.
이때 $\frac{f(t_{3})}{t_3} = f'(x)$를 만족시키는 양의 실수 $x$의 값은 $2$개이고, 그중 $k$가 아닌 값을 $s$라 하면 $6 \lt s \lt \frac{22}{3}$이므로 $g(t_{3}) = k$
그러므로 $\{ k\,|\,0 \lt k \lt \frac{4}{3} \} \subset \{ g(t) \,|\,2 \lt t \lt 6 \text{ 또는 } 6 \lt t \lt \alpha \}$ $\cdots\cdots$ ㉣
㉢, ㉣에 의하여
$\{ k\,|\,0 \lt k \lt \frac{4}{3} \} = \{ g(t) \,|\,2 \lt t \lt 6 \text{ 또는 } 6 \lt t \lt \alpha \}$
(ⅲ) $t = 6$일 때
ㄴ에 의하여 $g(6) = \frac{4}{3}$이므로 $\{ \frac{4}{3} \} = \{ g(t) \,|\, t=6 \}$
(ⅰ), (ⅱ), (ⅲ)에 의하여 함수 $g(t)$의 치역은
$\{ k \,|\,0 \lt k \le \frac{4}{3} \text{ 또는 } k \ge \frac{22}{3} \}$
그러므로 함수 $g(t)$의 치역의 원소가 아닌모든 자연수의 합은
$2+3+4+5+6+7 = 27$ (참)
따라서 옳은 것은 ㄱ, ㄴ, ㄷ
21. 모든 항이 자연수이고 다음 조건을 만족시키는 모든 수열 $\{ a_n \}$에 대하여 $a_1$의 최댓값과 최솟값을 각각 $M$, $m$이라 할 때, $M-m$의 값은? [4점]
(가) $a_{5} = 63$
(나) 모든 자연수 $n$에 대하여
$$a_{n+2} = \begin{cases} a_{n+1} + a_{n} & (a_{n+1}\times a_{n} \textbf{이 홀수인 경우}) \\ a_{n+1} + a_{n}-2 & (a_{n+1}\times a_{n} \textbf{이 짝수인 경우}) \end{cases}$$
이다.
① $16$
② $19$
③ $22$
④ $25$
⑤ $28$
④
조건 (나)에서
$a_{n}$이 홀수이고 $a_{n+1}$이 홀수이면 $a_{n+2}$는 짝수,
$a_{n}$이 홀수이고 $a_{n+1}$이 짝수이면 $a_{n+2}$는 홀수,
$a_{n}$이 짝수이고 $a_{n+1}$이 홀수이면 $a_{n+2}$는 홀수,
$a_{n}$이 짝수이고 $a_{n+1}$이 짝수이면 $a_{n+2}$는 짝수이다.
조건 (가)에서 $a_{5}$가 홀수이므로 $a_{3}$과 $a_{4}$ 중 하나는 홀수, 다른 하나는 짝수이어야 한다.
(ⅰ) $a_{3}$이 홀수이고 $a_{4}$가 짝수인 경우
$a_{2}$는 홀수이고 $a_{1}$은 짝수이다.
$a_{1} = 2k$, $a_{2} = 2l-1$ ($k$, $l$은 자연수)라 하면 조건 (나)에 의하여
$a_{1} \times a_{2}$는 짝수이므로 $a_{3} = 2k+2l-3$
$a_{2} \times a_{3}$은 홀수이므로 $a_{4} = 2k+4l-4$
$a_{3} \times a_{4}$는 짝수이므로 $a_{5} = 4k+6l-9$
$4k+6l-9 = 63$에서 $a_{1} = 2k = 36-3l$이므로 가능한 $a_{1}$의 값은
$6$, $12$, $18$, $24$, $30$이다.
(ⅱ) $a_{3}$이 짝수이고 $a_{4}$가 홀수인 경우
$a_{2}$는 홀수이고 $a_{1}$도 홀수이다.
$a_{1} = 2p-1$, $a_{2} = 2q-1$ ($p$, $q$는 자연수)라 하면 조건 (나)에 의하여
$a_{1} \times a_{2}$는 홀수이므로 $a_{3} = 2p+2q-2$
$a_{2} \times a_{3}$은 짝수이므로 $a_{4} = 2p+4q-5$
$a_{3} \times a_{4}$는 짝수이므로 $a_{5} = 4p+6q-9$
$4p+6q-9 = 63$에서 $a_{1} = 2p-1 = 35-3q$이므로 가능한 $a_1$의 값은
$5$, $11$, $17$, $23$, $29$이다.
(ⅰ), (ⅱ)에 의하여 $a_1$의 최댓값은 $30$, 최솟값은 $5$
따라서 $M-m = 30-5 = 25$

22. $\displaystyle \lim_{x \to 3}\frac{x-3}{\sqrt{x+1}-2}$의 값을 구하시오. [3점]
24. 함수 $f(x) = x^{3}+2x^{2}+2$에 대하여 $\displaystyle \lim_{x \to 1}\frac{1}{x-1}\int_{1}^{x}f'(t) dt$ 의 값을 구하시오. [3점]
25. 방정식 $\log_{2}x-3 = \log_{x}16$을 만족시키는 모든 실수 $x$의 값의 곱을 구하시오. [3점]
$8$
$\log_{x}16 = \dfrac{4}{\log_{2}x}$이므로
$\log_{2}x-3 = \log_{x}16$에서 $\log_{2}x-3 = \frac{4}{\log_{2}x}$
$(\log_{2}x)^{2}-3\log_{2}x-4 = 0$
$(\log_{2}x-4)(\log_{2}x+1) = 0$
$\log_{2}x = 4$ 또는 $\log_{2}x = -1$
$\log_{2}x = 4$에서 $x = 16$,
$\log_{2}x = -1$에서 $x = \frac{1}{2}$
따라서 구하는 모든 실수 $x$의 값의 곱은 $8$
26. 수직선 위를 움직이는 두 점 $\mathrm{P}$, $\mathrm{Q}$의 시각 $t$ ($t \gt 0$)에서의 위치가 각각 $$x_{1}(t) = t^{3}-3t^{2}-24t, \:x_{2}(t) = t^{2}-at$$ 이다. 두 점 $\mathrm{P}$, $\mathrm{Q}$의 운동 방향이 시각 $t=k$에서 동시에 바뀔 때, $a+k$의 값을 구하시오. (단, $a$와 $k$는 상수이다.) [4점]
$12$
두 점 $\mathrm{P}$, $\mathrm{Q}$의 시각 $t$ ($t \gt 0$)에서의 속도를 각각 $v_{1}(t)$, $v_{2}(t)$라 하면
$v_{1}(t) = 3t^{2}-6t-24$, $v_{2}(t) = 2t-a$
$v_{1}(t) = 3(t+2)(t-4) = 0$에서 $t = 4$
$0 \lt t \lt 4$에서 $v_{1}(t) \lt 0$, $t \gt 4$에서 $v_{1}(t) \gt 0$이므로 점 $\mathrm{P}$의 운동 방향은 시각 $t = 4$에서만 바뀐다.
또한 두 점 $\mathrm{P}$, $\mathrm{Q}$의 운동 방향이 동시에 바뀌므로 점 $\mathrm{Q}$의 운동 방향도 시각 $t = 4$에서 바뀌어야 한다.
$v_{2}(t) = 8-a = 0$에서 $a=8$
따라서 $a+k = 8+4 = 12$
27. 공차가 $d$인 등차수열 $\{ a_n \}$이 다음 조건을 만족시키도록 하는 모든 자연수 $d$의 값의 합을 구하시오. [4점]
(가) $a_{8} = 2a_{5}+10$
(나) 모든 자연수 $n$에 대하여 $a_{n}\times a_{n+1} \ge 0$이다.
$18$
구하는 수열 $\{ a_n \}$의 공차가 자연수이므로 $d \gt 0$
조건 (가)에서
$a_{1}+7d = 2(a_{1}+4d)+10$, $a_{1} = -d-10 \lt 0$
모든 자연수 $n$에 대하여 $a_{n} \lt a_{n+1}$이므로 $a_{n} \lt 0$을 만족시키는 자연수 $n$의 최댓값을 $k$라 하면 $a_{k+1} \ge 0$
그러므로 $a_{k}\times a_{l+1} \le 0$
그런데 조건 (나)에서 $a_{k}\times a_{l+1} \ge 0$이므로
$a_{k+1} = 0$
$a_{k+1} = (-d-10)+kd = 0$에서 $k = \frac{10}{d}+1$
$k$가 자연수이므로 $d$는 $10$의 약수이다.
따라서 구하는 모든 자연수 $d$의 값의 합은
$1+2+5+10 = 18$
28. 상수항과 계수가 모두 음이 아닌 정수인 두 다항함수 $f(x)$, $g(x)$가 다음 조건을 만족시킬 때, $f(2)+g(2)$의 값을 구하시오. [4점]
(가) $\displaystyle \lim_{x \to \infty}\frac{\{ f(x) \}^{2}g(x)}{x^{5}} = 4$
(나) $\displaystyle \lim_{x \to 0}\frac{ f(x)\{ g(x) \}^{2}}{x^{5}} = 2$
$16$
조건 (가)에서 함수 $\{ f(x) \}^{2}g(x)$의 차수가 $5$이므로 두 함수 $f(x)$, $g(x)$는 아래의 경우 중 하나이다.
(ⅰ) $f(x)$ : 상수함수, $g(x)$ : 오차함수
(ⅱ) $f(x)$ : 일차함수, $g(x)$ : 삼차함수
(ⅲ) $f(x)$ : 이차함수, $g(x)$ : 일차함수
조건 (나)에서 $\displaystyle \lim_{x \to \infty}\frac{ f(x)\{ g(x) \}^{2}}{x^{5}} = 2$이고
$\displaystyle \lim_{x \to 0}x^{5} = 0$이므로 $\displaystyle \lim_{x \to 0}f(x)\{ g(x) \}^{2} = 0$
그러므로 어떤 다항함수 $h(x)$에 대하여
$f(x)\{ g(x) \}^{2} = x^{k}h(x)$ (단, $k$는 자연수, $h(0) \ne 0$)
이때
$k \lt 5$이면 $\displaystyle \lim_{x \to 0}\frac{ f(x)\{ g(x) \}^{2}}{x^{5}}$의 값이 존재하지 않고
$k \gt 5$이면 $\displaystyle \lim_{x \to 0}\frac{ f(x)\{ g(x) \}^{2}}{x^{5}} = 0 \ne 2$이므로 $k = 5$
그러므로 $f(x)\{ g(x) \}^{2} = x^{5}h(x)$ ($h(0) \ne 0$) $\cdots\cdots$ ㉠
(ⅰ) $f(x)$ : 상수함수, $g(x)$ : 오차함수인 경우
다항식 $f(x)\{ g(x) \}^{2}$에서 오직 $g(x)$만이 $x$를 인수로 가지므로 ㉠을 만족시키지 않는다.
(ⅱ) $f(x)$ : 일차함수, $g(x)$ : 삼차함수인 경우
㉠을 만족시키기 위해서는
$f(x) = ax$, $g(x) = x^{2}(bx+c)$ (단, $a$, $b$, $c$는 음이 아닌 정수, $a \ne 0$, $b \ne 0$)
(ⅲ) $f(x)$ : 이차함수, $g(x)$ : 일차함수인 경우
다항식 $f(x)\{ g(x) \}^{2}$의 차수가 $4$이므로 ㉠을 만족시키지 않는다.
(ⅰ), (ⅱ), (ⅲ)에 의하여 두 함수 $f(x)$, $g(x)$는
$f(x) = ax$, $g(x) = x^{2}(bx+c)$ (단, $a$, $b$, $c$는 음이 아닌 정수, $a \ne 0$, $b \ne 0$)
조건 (가)에서
$\begin{align}\displaystyle \lim_{x \to \infty}\frac{\{ f(x) \}^{2}g(x)}{x^{5}} &= \lim_{x \to \infty}\frac{a^{2}x^{4}(bx+c)}{x^{5}} \\
&= \lim_{x \to \infty}\left( a^{2}b + \frac{a^{2}c}{x} \right) \\
&= a^{2}b = 4\end{align}$
조건 (나)에서
$\begin{align}\displaystyle \lim_{x \to 0}\frac{ f(x)\{ g(x) \}^{2}}{x^{5}} &= \lim_{x \to 0}\frac{ ax^{5}(bx+c)^{2}}{x^{5}} \\
&= \displaystyle \lim_{x \to 0}a(bx+c)^{2} \\
&= ac^{2} = 2\end{align}$
$a^{2}b = 4$, $ac^{2} = 2$를 만족시키는 음이 아닌 세 정수 $a$, $b$, $c$는
$a = 2$, $b = 1$, $c = 1$
그러므로 $f(x) = 2x$, $g(x) = x^{2}(x+1)$
따라서 $f(2) + g(2) = 4+4\times 3 = 16$
29. 두 상수 $a$, $b$ ($0 \le b \le \pi$)에 대하여 닫힌구간 $\bigg[ \dfrac{\pi}{2},\, a\bigg]$에서 함수 $f(x) = 2 \cos (3x+b)$의 최댓값은 $1$이고 최솟값은 $-\sqrt{3}$이다.
$a \times b = \dfrac{q}{p}\pi^{2}$일 때, $p+q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$14$
$\frac{\pi}{2} \le x \le a$인 $x$에 대하여 $\frac{3}{2}\pi+b \le 3x+b \le 3a+b$이므로 닫힌구간 $[\frac{\pi}{2}, a]$에서 함수 $f(x) = 2 \cos (3x+b)$의 최댓값,최솟값은 각각 닫힌구간 $[\frac{3}{2}\pi+b, 3a+b]$에서 함수 $y = 2 \cos x$의 최댓값,최솟값과 같다.
함수 $y = 2 \cos x$의 그래프는 그림과 같다. 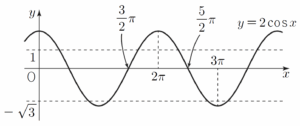 $0 \le b \le \pi$인 $b$에 대하여 $\frac{3}{2}\pi \le \frac{3}{2}\pi + b \le \frac{5}{2}\pi$이므로 닫힌구간 $[\frac{3}{2}\pi+b, 3a+b]$에서 함수 $y = 2 \cos x$최댓값이 $1$, 최솟값이 $-\sqrt{3}$이 되도록 하는 $a$, $b$는 $2\pi \lt \frac{3}{2}\pi + b \lt \frac{5}{2}\pi$, $\frac{5}{2}\pi \lt 3a + b \lt 3\pi$를 만족시켜야 한다.
$0 \le b \le \pi$인 $b$에 대하여 $\frac{3}{2}\pi \le \frac{3}{2}\pi + b \le \frac{5}{2}\pi$이므로 닫힌구간 $[\frac{3}{2}\pi+b, 3a+b]$에서 함수 $y = 2 \cos x$최댓값이 $1$, 최솟값이 $-\sqrt{3}$이 되도록 하는 $a$, $b$는 $2\pi \lt \frac{3}{2}\pi + b \lt \frac{5}{2}\pi$, $\frac{5}{2}\pi \lt 3a + b \lt 3\pi$를 만족시켜야 한다.
닫힌구간 $[\frac{3}{2}\pi+b, 3a+b]$에서 함수 $y = 2 \cos x$는 $x$의 값이 증가하면 $y$의 값은 감소하므로 닫힌구간 $[\frac{3}{2}\pi+b, 3a+b]$에서 함수 $y = 2 \cos x$의 최댓값은 $2 \cos (\frac{3}{2}\pi + b)$, 최솟값은 $2 \cos (3a+b)$이다.
$2 \cos (\frac{3}{2}\pi + b) = 1$에서 $\frac{3}{2}\pi + b = \frac{7}{3}\pi$, $b = \frac{5}{6}\pi$
$2 \cos (3a+b) = -\sqrt{3}$에서 $3a+b = \frac{17}{6}\pi$, $a = \frac{2}{3}\pi$
$a \times b = \frac{2}{3}\pi \times \frac{5}{6}\pi = \frac{5}{9}\pi^{2}$
따라서 $p = 9$, $q = 5$이며 $p+q = 14$
30. 최고차항의 계수가 양수이고 $f'(2) \lt 0$인 삼차함수 $f(x)$에 대하여 함수 $g(x)$가 $$g(x) = \begin{cases}\displaystyle \int_{0}^{x}f(t) dt-4 & (x \lt 2) \\ \\ \displaystyle -\int_{0}^{x}f(t) dt+4 & (x \ge 2) \end{cases}$$ 이고 다음 조건을 만족시킨다.
(가) $\displaystyle \lim_{x \to 2-}\frac{g(x)-4}{x-2}$ $=\displaystyle \lim_{x \to 2+}\frac{g(x)+4}{x-2} = g'(0)$
(나) 방정식 $g(x) = 4$는 서로 다른 두 실근을 갖는다.
$f(5)$의 값을 구하시오. [4점]
$30$
$F(x) = \int_{0}^{x}f(t)dt$라 하면 $F(x)$는 최고차항의 계수가 양수인 사차함수이다.
$g(x) = \begin{cases} F(x)-4 & (x \lt 2) \\ -F(x)+4 & (x \ge 2) \end{cases}$
조건(가)에서 $\displaystyle \lim_{x \to 2-}\frac{g(x)-4}{x-2} = g'(0)$이고 $\displaystyle \lim_{x \to 2-}(x-2) = 0$이므로 $\displaystyle \lim_{x \to 2-}\{ g(x)-4 \} = \lim_{x \to 2-}\{ F(x)-8 \} = F(2)-8 = 0$
그러므로 $F(2) = 8$ $\cdots\cdots$ ㉠
또한
$\displaystyle \lim_{x \to 2-}\frac{g(x)-4}{x-2} = \displaystyle \lim_{x \to 2-}\frac{F(x)-8}{x-2} = F'(2) = f(2)$
$\displaystyle \lim_{x \to 2+}\frac{g(x)+4}{x-2} = \lim_{x \to 2+}\frac{-\{ F(x)-8 \}}{x-2} = -F'(2) = -f(2)$
$g'(0) = F'(0) = f(0)$
조건 (가)에 의하여 $f(2) = -f(2) = f(0)$에서
$f(2) = f(0) = 0$
$f(x) = ax(x-2)(x-b)$ ($a$, $b$는 상수, $a \gt 0$)
$f(x) = a\{ x^{3}-(b+2)x^{2}+2bx \}$에서
$f'(x) = a\{ 3x^{2}-2(b+2)x+2b \}$
$f'(2) = a(-2b+4) \lt 0$에서
$a \gt 0$이므로 $-2b+4 \lt 0$, $b \gt 2$
함수 $y = f(x)$의 그래프는 그림과 같다. 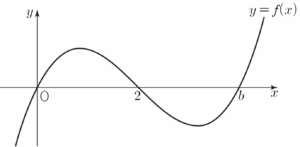 $g'(x) = \begin{cases} f(x) & (x \lt 2) \\ -f(x) & (x \gt 2) \end{cases}$
$g'(x) = \begin{cases} f(x) & (x \lt 2) \\ -f(x) & (x \gt 2) \end{cases}$
$f(x) = ax(x-2)(x-b)$ ($a \gt 0$, $b \gt 2$)에 대하여 함수 $g(x)$의 증가와 감소를 표로 나타내면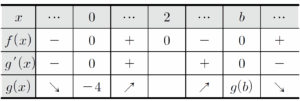
$\displaystyle \lim_{x \to 2-}g(x) = 4$, $\displaystyle \lim_{x \to 2+}g(x) = g(2) = -4$
조건 (나)에 의하여 함수 $y = g(x)$의 그래프와 직선 $y = 4$가 두 점에서 만나야 하므로 $g(b) = 4$
함수 $y = g(x)$의 그래프는 그림과 같다. 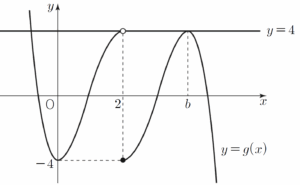 $g(b) = -\int_{0}^{b}f(t)dt+4 = 4$에서 $\int_{0}^{b}f(t)dt = 0$
$g(b) = -\int_{0}^{b}f(t)dt+4 = 4$에서 $\int_{0}^{b}f(t)dt = 0$
$\int_{0}^{b}at(t-2)(t-b)dt$
$= \int_{0}^{b}a\{ t^{3}-(b+2)t^{2}+2bt \}dt$
$= a\bigg[ \frac{1}{4}t^{4}-\frac{b+2}{3}t^{3}+bt^{2} \bigg]_{0}^{b}$
$= a\left( \frac{b^4}{4}-\frac{b+2}{3}\times b^{3} + b^{3} \right)$
$= ab^{3} \left( \frac{b}{4}-\frac{b+2}{3}+1 \right) = 0$
$3b-4(b+2)+12 = 0$에서 $b = 4$
㉠에 의하여 $\int_{0}^{2}f(t)dt = 8$
$\int_{0}^{2}f(t)dt$
$= \int_{0}^{2}at(t-2)(t-4)dt$
$= a\bigg[ \frac{1}{4}t^{4}-2t^{3}+4t^{2} \bigg]_{0}^{2}$
$= 4a = 8$
에서 $a = 2$이므로 $f(x) = 2x(x-2)(x-4)$
따라서 $f(5) = 30$



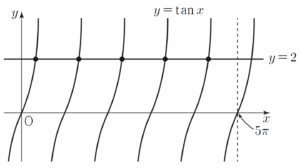 따라서 $0 \lt x \lt 5 \pi$에서 함수 $y = \tan x$의 그래프와 직선 $y = 2$가 만나는 점의 개수는 $5$
따라서 $0 \lt x \lt 5 \pi$에서 함수 $y = \tan x$의 그래프와 직선 $y = 2$가 만나는 점의 개수는 $5$