24년 10월 고2 교육청


① $1$
② $2$
③ $4$
④ $8$
⑤ $16$
① $8$
② $9$
③ $10$
④ $11$
⑤ $12$
① $2$
② $4$
③ $6$
④ $8$
⑤ $10$
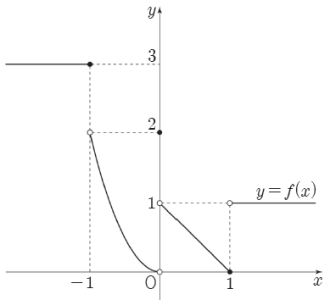
4. 함수 $y = f(x)$의 그래프가 그림과 같다.
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
① $\frac{3}{2}$
② $2$
③ $\frac{5}{2}$
④ $3$
⑤ $\frac{7}{2}$
①
$x \gt \dfrac{1}{2}$인 모든 실수 $x$에 대하여
$\frac{3}{2x + 1} \lt f(x) \lt \frac{3}{2x-1}$이므로
$\frac{3x}{2x + 1} \lt xf(x) \lt \frac{3x}{2x-1}$
이때
$\displaystyle \lim_{x \to \infty}\frac{3x}{2x + 1} = \lim_{x \to \infty}\frac{3x}{2x-1} = \frac{3}{2}$
이므로
함수의 극한의 대소 관계에 의하여
$\displaystyle \lim_{x \to \infty}xf(x) = \frac{3}{2}$
① $7$
② $9$
③ $11$
④ $13$
⑤ $15$
① $-2$
② $-1$
③ $0$
④ $1$
⑤ $2$
③
함수 $f(x)$가 $x = 2$에서 미분가능하므로 함수 $f(x)$는 $x = 2$에서 연속이다.
$\displaystyle \lim_{x \to 2-}f(x) = \lim_{x \to 2+}f(x) = f(2)$에서
$2-a = 4 + 2b + a$, $b = -a-1$
$\displaystyle \lim_{x \to 2-}\dfrac{f(x)-f(2)}{x-2}$
$=\displaystyle \lim_{x \to 2-}\dfrac{(x-a)-(2-a)}{x-2} = \lim_{x \to 2-}\dfrac{x-2}{x-2} = 1$
$\displaystyle \lim_{x \to 2+}\dfrac{f(x)-f(2)}{x-2}$
$=\displaystyle \lim_{x \to 2+}\dfrac{(x^{2} + bx + a)-(2-a)}{x-2} = \lim_{x \to 2+}\dfrac{x^{2}-(a + 1)x+2(a-1)}{x-2}$
$=\displaystyle \lim_{x \to 2+}\dfrac{(x-2)(x-a + 1)}{x-2} = \lim_{x \to 2+}(x-a + 1) = 3-a$
함수 $f(x)$가 $x = 2$에서 미분가능하므로
$1 = 3-a$에서 $a = 2$, $b = -3$
따라서 $f(2) = 0$
① $\frac{1}{5}$
② $\frac{4}{15}$
③ $\frac{1}{3}$
④ $\frac{2}{5}$
⑤ $\frac{7}{15}$
① $4$
② $2 + \log_{2}5$
③ $3 + \log_{2}3$
④ $2 + \log_{2}7$
⑤ $5$
① $40$
② $44$
③ $48$
④ $52$
⑤ $56$
③
등비수열 $\{a_n\}$의 공비를 $r$ ($r \ne 0$)이라 하자.
$a_{1} = 0$이면 $\displaystyle \sum_{k = 1}^{5}a_{k} = 0 \ne 33$이므로 $a_{1} \ne 0$
$a_{3} + 2a_{4} = a_{1}r^{2} + 2a_{1}r^{3} = a_{1}r^{2}(1 + 2r) = 0$에서
$r = -\frac{1}{2}$
$\displaystyle \sum_{k = 1}^{5}a_{k} = \dfrac{a_{1}\{ 1-(-\frac{1}{2})^{5}\}}{1-(-\frac{1}{2})} = \frac{11}{16}a_{1} = 33$
따라서 $a_{1} = 48$
① $-\frac{2}{3}$
② $-\frac{1}{3}$
③ $0$
④ $\frac{1}{3}$
⑤ $\frac{2}{3}$
②
$\cos(\frac{3}{2}\pi-\theta) = -\sin \theta$, $\tan \theta = \frac{\sin \theta}{\cos \theta}$이므로
$\cos(\frac{3}{2}\pi-\theta) \times \tan \theta$
$= -\sin \theta \times \frac{\sin \theta}{\cos \theta} = -\frac{\sin^{2} \theta}{\cos \theta} = \frac{8}{3}$
$\sin^{2}\theta + \cos^{2}\theta = 1$이므로 $\frac{\cos^{2} \theta-1}{\cos \theta} = \frac{8}{3}$
$3 \cos^{2} \theta-8\cos \theta-3 = 0$
$(\cos \theta-3)(3\cos \theta + 1) = 0$
$-1 \le \cos \theta \le 1$이므로 $\cos \theta = -\dfrac{1}{3}$
① $45$
② $48$
③ $51$
④ $54$
⑤ $57$
①
$\displaystyle a_{2n} = \sum_{k=1}^{2n-1}(k-a_{k}) = \sum_{k=1}^{2n-1}k-\sum_{k=1}^{2n-1}a_{k}$
$\displaystyle a_{2n} + \sum_{k=1}^{2n-1}a_{k} = \sum_{k=1}^{2n-1}k$에서
$\displaystyle \sum_{k=1}^{2n}a_{k} = \sum_{k=1}^{2n-1}k$
따라서 $\displaystyle \sum_{k=1}^{10}a_{k} = \sum_{k=1}^{9}k$ $= \dfrac{9 \times 10}{2} = 45$
① $\frac{\sqrt{3}-1}{2}$
② $\frac{2\sqrt{3}-1}{4}$
③ $\frac{\sqrt{3}}{2}$
④ $\frac{2\sqrt{3}+1}{4}$
⑤ $\frac{\sqrt{3}+1}{2}$
⑤
점 $\mathrm{P}$의 $x$좌표를 $a$ ($a \gt 0$)이라 하면 점 $\mathrm{P}$의 좌표는 $\mathrm{P}(a, a+1)$
각의 크기 $\theta$를 나타내는 동경과 각의 크기 $7\theta$를 나타내는 동경이 일치하므로
$7\theta = \theta + 2n\pi$ ($n$은 정수)
$\theta = \frac{n}{3}\pi$
이때 점 $\mathrm{P}$는 제$\,1\,$사분면 위의 점이고
$0 \lt \theta \lt 2\pi$이므로 $n = 1$, $\theta = \frac{\pi}{3}$
$\tan \frac{\pi}{3} = \frac{a+1}{a}$에서
$\sqrt{3}a = a+1$, $(\sqrt{3}-1)a = 1$
따라서 $a = \frac{1}{\sqrt{3}-1} = \dfrac{\sqrt{3} + 1}{2}$
① $-7$
② $-3$
③ $1$
④ $5$
⑤ $9$
②
조건 (가)의 식의 양변에 $x = 0$을 대입하면
$0 \times f(0) = b$에서 $b = 0$
조건 (가)의 식의 양변에 $x = 4$를 대입하면
$2f(4) = 16 + 4a$
조건 (나)에 의하여 $4 = 16 + 4a$에서 $a = -3$
그러므로 $x \ge -\frac{1}{2}$이고 $x \ne 0$인 모든 실수 $x$에 대하여
$f(x) = \dfrac{x(x-3)}{\sqrt{2x + 1}-1}$
함수 $f(x)$가 실수 전체의 집합에서 연속이므로 함수 $f(x)$는 $x = 0$에서 연속이다.
따라서
$f(0) = \displaystyle \lim_{x \to 0}f(x)$
$= \displaystyle \lim_{x \to 0}\dfrac{x(x-3)}{\sqrt{2x + 1}-1}$
$= \displaystyle \lim_{x \to 0}\dfrac{x(x-3)(\sqrt{2x + 1}+1)}{(\sqrt{2x + 1}-1)(\sqrt{2x + 1}+1)}$
$= \displaystyle \lim_{x \to 0}\dfrac{x(x-3)(\sqrt{2x + 1}+1)}{2x}$
$= \displaystyle \lim_{x \to 0}\dfrac{(x-3)(\sqrt{2x + 1}+1)}{2}$
$= \dfrac{-3 \times 2}{2} = -3$
① $5$
② $6$
③ $7$
④ $8$
⑤ $9$
⑤
(ⅰ) $n$이 홀수일 때
$f(n) = 1$이므로 $f(3) = f(5) = f(7) = f(9) = 1$
(ⅱ) $n$이 짝수일 때
$n = 2$, $n = 4$이면 $\sin \frac{n}{5}\pi \gt 0$이므로 $f(2) = f(4) = 2$
$n = 6$, $n = 8$이면 $\sin \frac{n}{5}\pi \lt 0$이므로 $f(6) = f(8) = 0$
$n = 10$이면 $\sin \frac{10}{5}\pi = 0$이므로 $f(10) = 1$
(ⅰ), (ⅱ)에 의하여 $\displaystyle \sum_{n=2}^{10}f(n) = 1 \times 4 + 2 \times 2 + 1 = 9$
① $96$
② $100$
③ $104$
④ $108$
⑤ $112$
④
$\log_{n}4 \times \bigg( \dfrac{4}{\log_{m}2} + \log_{2}n \bigg)$
$= 2\log_{n}2 \times (4 \log_{2}m + \log_{2}n)$
$= 8\log_{n}2 \times \log_{2}m + 2\log_{n}2 \times \log_{2}n$
$= 8\log_{n}m + 2 = 8$
$\log_{n}m = \frac{3}{4}$에서 $m = n^{\frac{3}{4}}$
$n^{\frac{3}{4}}$이 자연수가 되기 위해서는 어떤 자연수 $k$에 대하여 $n = k^{4}$이어야 한다.
$1 \lt n \lt 100$이므로 $n = 2^{4}$ 또는 $n = 3^{4}$이다.
$n = 2^{4}$이면 $m = (2^{4})^{\frac{3}{4}} = 2^{3} = 8$이므로
$m + n = 8 + 16 = 24$
$n = 3^{4}$이면 $m = (3^{4})^{\frac{3}{4}} = 3^{3} = 27$이므로
$m + n = 27 + 81 = 108$
따라서 $m + n$의 최댓값은 $108$
① $\frac{3}{8}\pi$
② $\frac{\pi}{2}$
③ $\frac{5}{8}\pi$
④ $\frac{3}{4}\pi$
⑤ $\frac{7}{8}\pi$
①
$f(x) = \cos^{2}x-\sin x-1 = (1-\sin^{2}x)-\sin x-1$
$= -\sin^{2}x-\sin x$ $=-(\sin x + \frac{1}{2})^{2} + \frac{1}{4}$
$f(\pi) = 0$이고 $\pi$가 구간 $(\pi, a\,]$에 속하지 않으므로 구간 $(\pi, a\,]$에서 함수 $f(x)$가 최솟값을 갖기 위해서는 $f(x) \le 0$을 만족시키는 $x$의 값이 구간 $(\pi, a\,]$에 존재해야 한다.
$f(x) \le 0$에서 $\sin x = -1$ 또는 $\sin x \ge 0$
$x \gt \pi$에서 $\sin x = -1$인 $x$의 최솟값은 $\frac{3}{2}\pi$
$x \gt \pi$에서 $\sin x \ge 0$인 $x$의 최솟값은 $2\pi$
그러므로 $p = \frac{3}{2}\pi$
한편 구간 $(\pi, \,\frac{3}{2}\pi\,]$에서 $-1 \le \sin x \lt 0$이므로
$f(x) = -(\sin x + \frac{1}{2})^{2} + \frac{1}{4} \le \frac{1}{4}$
그러므로 $M = \frac{1}{4}$
따라서 $p \times M = \dfrac{3}{8}\pi$
① $4\sqrt{2}$
② $5\sqrt{3}$
③ $12$
④ $7\sqrt{5}$
⑤ $8\sqrt{6}$
②
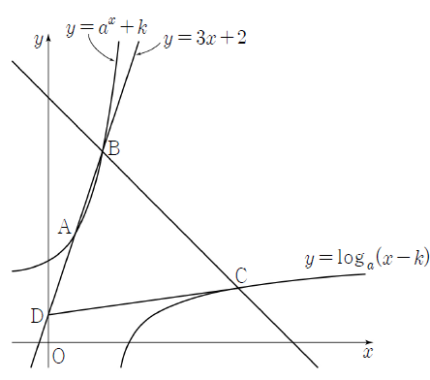
점 $\mathrm{A}$의 좌표를 $\mathrm{A}(p, 3p+2)$라 하면 점 $\mathrm{B}$는 선분 $\mathrm{DA}$를 $2 : 1$로 외분하는 점이므로 점 $\mathrm{B}$의 좌표는 $\mathrm{B}(2p, 6p+2)$이다.
함수 $y = a^{x} + k$의 그래프와 함수 $y = \log_{a}(x-k)$의 그래프는 직선 $y = x$에 대하여 서로 대칭이고, 곡선 $y = a^{x} + k$ 위의 점 $\mathrm{B}$와 곡선 $y = \log_{a}(x-k)$ 위의 점 $\mathrm{C}$를 지나는 직선이 직선 $y = x$와 서로 수직이므로 점 $\mathrm{C}$는 점 $\mathrm{B}$를 직선 $y = x$에 대하여 대칭이동시킨 점이다.
그러므로 점 $\mathrm{C}$의 좌표는 $\mathrm{C}(6p+2, 2p)$이다.
삼각형 $\mathrm{CBD}$는 이등변삼각형이므로 두 직선 $\mathrm{BD}$, $\mathrm{AC}$는 서로 수직이다.
직선 $\mathrm{BD}$의 기울기가 $3$이므로 직선 $\mathrm{AC}$의 기울기는
$\dfrac{2p-(3p+2)}{(6p+2)-p} = \dfrac{-p-2}{5p+2} = -\dfrac{1}{3}$에서 $p = 2$
그러므로 $\mathrm{A}(2, 8)$, $\mathrm{B}(4, 14)$
점 $\mathrm{A}$가 곡선 $y = a^{x} + k$ 위의 점이므로 $a^{2} + k = 8$
점 $\mathrm{B}$가 곡선 $y = a^{x} + k$ 위의 점이므로 $a^{4} + k = 14$
두 식을 연립하면
$a^{4}-a^{2}-6 = 0$, $(a^{2}+2)(a+\sqrt{3})(a-\sqrt{3}) = 0$
$a \gt 1$이므로 $a = \sqrt{3}$, $k = 5$
따라서 $a \times k = 5\sqrt{3}$
① $\frac{6}{5}\pi$
② $\frac{7}{5}\pi$
③ $\frac{8}{5}\pi$
④ $\frac{9}{5}\pi$
⑤ $2\pi$
③
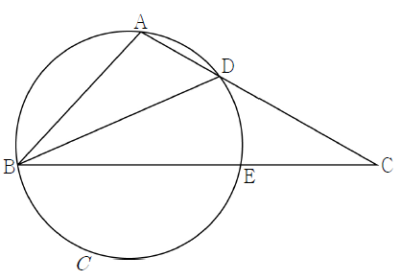
두 호 $\mathrm{AD}$, $\mathrm{DE}$의 길이가 같으므로 두 호 $\mathrm{AD}$, $\mathrm{DE}$에 대한 원주각의 크기가 같다.
$\angle \mathrm{DBA} = \angle \mathrm{EBD} = \theta$, $\overline{\mathrm{AD}} = k$라 하면
$\overline{\mathrm{AB}} : \overline{\mathrm{BC}} = \overline{\mathrm{AD}} : \overline{\mathrm{CD}}$이므로 $\overline{\mathrm{CD}} = 2k$
삼각형 $\mathrm{ABD}$에서 코사인법칙에 의하여
$k^{2} = 2^{2} + \sqrt{6}^{2}-2 \times 2 \times \sqrt{6} \times \cos \theta$
$k^{2} = 10-4\sqrt{6}\cos \theta$ $\cdots\cdots$ ㉠
삼각형 $\mathrm{BCD}$에서 코사인법칙에 의하여
$(2k)^{2} = \sqrt{6}^{2} + 4^{2}-2 \times \sqrt{6} \times 4 \times \cos \theta$
$2k^{2} = 11-4\sqrt{6}\cos \theta$ $\cdots\cdots$ ㉡
㉠, ㉡을 연립하면 $k = 1$, $\cos \theta = \frac{3}{8}\sqrt{6}$
$\sin \theta = \sqrt{1-(\frac{3}{8}\sqrt{6})^{2}} = \frac{\sqrt{10}}{8}$
원 $C$의 반지름의 길이를 $R$이라 하면 삼각형 $\mathrm{ABD}$에서 사인법칙에 의하여
$\dfrac{\overline{AD}}{\sin \theta} = 2R$에서 $R = \frac{2}{5}\sqrt{10}$
따라서 원 $C$의 넓이는 $\pi \times (\frac{2}{5}\sqrt{10})^{2} = \dfrac{8}{5}\pi$
① ㄱ
② ㄴ
③ ㄱ,ㄴ
④ ㄱ,ㄷ
⑤ ㄴ,ㄷ
④
$f(0) = a$이므로 양수 $t$에 대하여
$g(t) = \dfrac{f(t)-f(0)}{t-0} = \dfrac{f(t)-a}{t}$
이고, 함수 $g(t)$의 값은 두 점 $(0, a)$, $(t, f(t))$를 지나는 직선의 기울기와 같다.
ㄱ.
$a = 1$일 때 $g(t) = \frac{f(1)-1}{1} = -1$ (참)
ㄴ.
(ⅰ) $a \ge 1$일 때 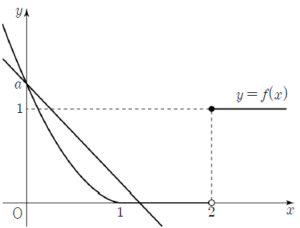 모든 양수 $t$에 대하여 $f(t) \le a$이므로 $g(t) = \frac{f(t)-a}{t} \le 0$
모든 양수 $t$에 대하여 $f(t) \le a$이므로 $g(t) = \frac{f(t)-a}{t} \le 0$
그러므로 함수 $g(t)$의 최댓값은 $1$이 될 수 없다.
(ⅱ) $-1 \lt a \lt 1$일 때 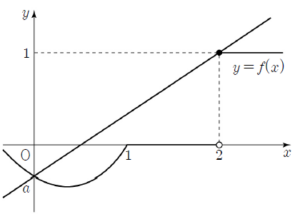 함수 $g(t)$는 $t = 2$일 때 최댓값을 갖는다.
함수 $g(t)$는 $t = 2$일 때 최댓값을 갖는다.
$g(2) = \frac{f(2)-a}{2} = \frac{1-a}{2} \lt 1$
그러므로 함수 $g(t)$의 최댓값은 $1$ 보다 작다.
(ⅲ) $a \le -1$일 때 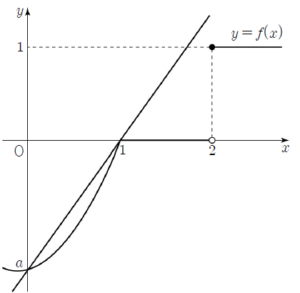 함수 $g(t)$는 $t = 1$일 때 최댓값을 갖는다.
함수 $g(t)$는 $t = 1$일 때 최댓값을 갖는다.
$g(1) = \frac{f(1)-a}{1} = -a$
함수 $g(t)$의 최댓값이 $1$이기 위해서는 $a = -1$
이때 $g(2) = \frac{f(2)-a}{2} = \frac{1-(-1)}{2} = 1$
(ⅰ), (ⅱ), (ⅲ)에 의하여
함수 $g(t)$의 최댓값이 $1$일 때, $g(2) = 1$ (거짓)
ㄷ.
$0 \lt k \lt 2$인 $k$에 대하여 두 점 $(0, a)$, $(k, f(k))$를 지나는 직선을 $l$이라 하자. $g(k) = g(k+1) = g(k+2)$인 양수 $k$ ($0 \lt k \lt 2$)가 존재하기 위해서는 함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $(0, a)$가 아닌 점이 $3$개이어야 하고, 이 세 교점의 $x$좌표는 $k$, $k+1$, $k+2$이어야 한다.
(ⅰ) $a \gt 0$일 때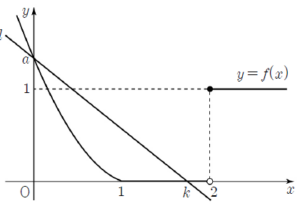 함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $x$좌표가 양수인 점은 $(k, f(k))$뿐이므로 $g(k) = g(k+1) = g(k+2)$인 $k$가 존재하지 않는다.
함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $x$좌표가 양수인 점은 $(k, f(k))$뿐이므로 $g(k) = g(k+1) = g(k+2)$인 $k$가 존재하지 않는다.
(ⅱ) $a = 0$일 때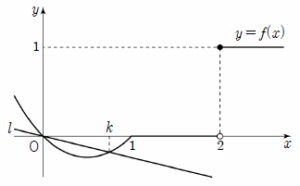 $0 \lt k \lt 1$일 때, 함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $x$좌표가 양수인 점은 $(k, f(k))$ 뿐이므로 $g(k) = g(k+1) = g(k+2)$인 $k$가 존재하지 않는다.
$0 \lt k \lt 1$일 때, 함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $x$좌표가 양수인 점은 $(k, f(k))$ 뿐이므로 $g(k) = g(k+1) = g(k+2)$인 $k$가 존재하지 않는다.
$1 \le k \lt 2$일 때, 직선 $l$의 기울기가 $0$이므로 $g(k) = 0$
이때 $g(k+1) = \frac{1-0}{(k+1)-0} = \frac{1}{k+1} \gt 0$이므로 $g(k) \ne g(k+1)$
그러므로 $g(k) = g(k+1) = g(k+2)$인 $k$가 존재하지 않는다.
(ⅲ) $a \lt 0$일 때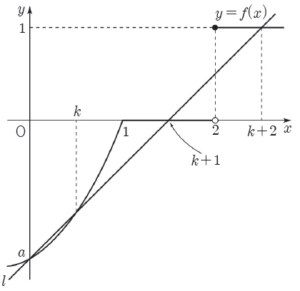 함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $(0, a)$가 아닌 점이 $3$개이기 위해서는 $0 \lt k \lt 1$이고 $f(k+1) = 0$, $f(k+2) = 1$이어야 한다.
함수 $y = f(x)$의 그래프와 직선 $l$의 교점 중 $(0, a)$가 아닌 점이 $3$개이기 위해서는 $0 \lt k \lt 1$이고 $f(k+1) = 0$, $f(k+2) = 1$이어야 한다.
$\frac{1-0}{(k+2)-(k+1)} = 1$이므로 직선 $l$의 기울기는 $1$
직선 $l$ 위의 두 점 $(k, f(k))$, $(k+1, 0)$에 대하여 $\frac{0-f(k)}{(k+1)-k} = 1$에서 $f(k) = -1$
즉, $(k-1)(k-a) = -1$ $\cdots\cdots$ ㉠
직선 $l$ 위의 두 점 $(0, a)$, $(k, f(k))$에 대하여 $\frac{f(k)-a}{k-0} = \frac{-1-a}{k} =1$에서
$a = -k-1$ $\cdots\cdots$ ㉡
㉠, ㉡을 연립하면 $(k-1)(2k+1) = -1$, $2k^{2}-k = 0$
$0 \lt k \lt 1$이므로 $k = \frac{1}{2}$, $a = -\frac{3}{2}$
그러므로
$f(x) = \begin{cases} \,(x-1)(x+ \frac{3}{2}) & (x \lt 1) \\ \:\:\:\:\:0 & (1 \le x \lt 2) \\ \:\:\:\:\: 1 & (x \ge 2) \end{cases}$
이때
$(x-1)(x+ \frac{3}{2}) = x^{2} + \frac{1}{2}x-\frac{3}{2}$
$= (x+\frac{1}{4})^{2}-\frac{25}{16} \ge -\frac{25}{16}$
함수 $y = f(x)$의 최솟값 $-\frac{25}{16}$가 $-\frac{3}{2}$ 보다 작으므로 함수 $y = f(x)$의 그래프와 직선 $y = -\frac{3}{2}$은 서로 다른 두 점에서
만난다. (참)
따라서 옳은 것은 ㄱ, ㄷ
① $\frac{92}{5}$
② $\frac{94}{5}$
③ $\frac{96}{5}$
④ $\frac{98}{5}$
⑤ $20$
③
$a_{1} \ge 2$이므로 모든 자연수 $n$에 대하여 $a_{n} \gt 0$
$a_{2} = \frac{1}{2}a_{1} \ge 1$이므로 $a_{3} = \frac{1}{4}a_{1}$
$a_{5} \lt 1$이라 하면 $a_{6} = \frac{1}{2}(a_{5} + a_{1})$에서
$a_{5} + 2a_{6} = 2a_{5} + a_{1} \gt 2$이므로 $a_{5} \ge 1$
그러므로 $a_{6} = \frac{1}{2}a_{5}$이고 $a_{5} + 2a_{6} = 2a_{5} = 2$에서
$a_{5} = 1$
$a_{4} \lt 1$이라 하면 $a_{5} = \frac{1}{2}(a_{4} + a_{1}) = 1$에서
$a_{4} = 2-a_{1} \le 0$이므로 $a_{4} \ge 1$
그러므로 $a_{5} = \frac{1}{2}a_{4} = 1$에서 $a_{4} = 2$
(ⅰ) $a_{1} \ge 4$일 때
$a_{3} = \frac{1}{4}a_{1} \ge 1$이므로 $a_{4} = \frac{1}{8}a_{1} = 2$에서
$a_{1} = 16$
(ⅱ) $a_{1} \lt 4$일 때
$a_{3} = \frac{1}{4}a_{1} \lt 1$이므로 $a_{4} = \frac{1}{2}(a_{3} + a_{1}) = \frac{5}{8}a_{1} = 2$에서
$a_{1} = \frac{16}{5}$
(ⅰ),(ⅱ)에 의하여 모든 $a_1$의 값의 합은
$16 + \frac{16}{5} = \dfrac{96}{5}$

$34$
$f(x)$가 다항함수이고 $\displaystyle \lim_{x \to \infty} \frac{f(x)-2x^{3}}{x^{2}} = 3$이므로
$f(x) = 2x^{3} + 3x^{2} + ax + b$ ($a$, $b$는 상수)
$\displaystyle \lim_{x \to 0} \frac{f(x)}{x} = 3$이고 $\displaystyle \lim_{x \to 0} x = 0$이므로 $\displaystyle \lim_{x \to 0} f(x) = 0$
그러므로 $b = 0$
$\displaystyle \lim_{x \to 0} \frac{f(x)}{x}$
$= \displaystyle \lim_{x \to 0} \frac{2x^{3} + 3x^{2} + ax}{x}$
$= \displaystyle \lim_{x \to 0} (2x^{2} + 3x + a) = a = 3$
그러므로 $f(x) = 2x^{3} + 3x^{2} + 3x$
따라서 $f(2) = 34$
$6$
$\log_{|a|}(-a^{2}-4a+21)$의 밑이 $|\,a\,|$이므로
$|\,a\,| \gt 0$이고 $|\,a\,| \ne 1$ $\cdots\cdots$ ㉠
$\log_{|a|}(-a^{2}-4a+21)$의 진수가 $-a^{2}-4a+21$이므로 $-a^{2}-4a+21 \gt 0$
$a^{2}+4a-21 = (a+7)(a-3) \lt 0$ $\cdots\cdots$ ㉡
㉠, ㉡을 동시에 만족시키는 정수 $a$는
$-6$, $-5$, $-4$, $-3$, $-2$, $2$
따라서 구하는 정수 $a$의 개수는 $6$
$385$
$n \ge 2$인 모든 자연수 $n$에 대하여
$\displaystyle \sum_{k = 1}^{n-1}(\sqrt{a_{k}}-\sqrt{a_{k+1}})$
$= (\sqrt{a_{1}}-\sqrt{a_{2}})+(\sqrt{a_{2}}-\sqrt{a_{3}})+ \cdots +(\sqrt{a_{n-1}}-\sqrt{a_{n}})$
$= \sqrt{a_{1}}-\sqrt{a_{n}} = \dfrac{n-1}{n}$
$a_{1} = 1$이므로 $n \ge 2$일 때 $\sqrt{a_{n}} = 1 – \frac{n-1}{n} = \frac{1}{n}$
그러므로 모든 자연수 $n$에 대하여 $a_{n} = \dfrac{1}{n^2}$
따라서 $\displaystyle \sum_{k = 1}^{10}\frac{1}{a_{k}}$ $= \displaystyle \sum_{k = 1}^{10}k^{2} = \frac{10 \times 11 \times 21}{6} = 385$
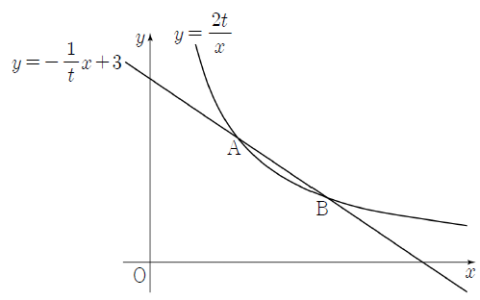
$54$
$\dfrac{2t}{x} = -\dfrac{1}{t}x + 3$에서 $2t^{2} = -x^{2} + 3tx$
$x^{2}-3tx+2t^{2} = 0$, $(x-t)(x-2t) = 0$
그러므로 두 점 $\mathrm{A}$, $\mathrm{B}$의 좌표는 $\mathrm{A}(t, 2)$, $\mathrm{B}(2t, 1)$
$\overline{\mathrm{OA}} = \sqrt{t^{2} + 4}$, $\overline{\mathrm{OB}} = \sqrt{4t^{2} + 1}$
$\displaystyle \lim_{t \to 1+}\frac{\overline{\mathrm{OB}}-\overline{\mathrm{OA}}}{t-1}$
$= \displaystyle \lim_{t \to 1+}\frac{\sqrt{4t^{2} + 1}-\sqrt{t^{2} + 4}}{t-1}$
$= \displaystyle \lim_{t \to 1+}\frac{(\sqrt{4t^{2} + 1}-\sqrt{t^{2} + 4})(\sqrt{4t^{2} + 1}+\sqrt{t^{2} + 4})}{(t-1)(\sqrt{4t^{2} + 1}+\sqrt{t^{2} + 4})}$
$= \displaystyle \lim_{t \to 1+}\frac{3(t^{2}-1)}{(t-1)(\sqrt{4t^{2} + 1}+\sqrt{t^{2} + 4})}$
$= \displaystyle \lim_{t \to 1+}\frac{3(t+1)}{\sqrt{4t^{2} + 1}+\sqrt{t^{2} + 4}}$
$= \dfrac{3}{5}\sqrt{5}$
따라서 $30 \times k^{2} = 30 \times (\frac{3}{5}\sqrt{5})^{2} = 54$
$22$
$a_{k} + a_{k+1} + a_{k+2} = 3a_{k+1}= 21$에서 $a_{k+1}= 7$
등차수열 $\{a_n\}$의 공차를 $d$ ($d$는 자연수)라 하자.
$a_{1} = a_{k+1}-dk = 7-dk$,
$a_{k+4} = a_{k+1}+3d = 7+3d$이므로
$S_{k+4} = \dfrac{(k+4)(a_{1}+a_{k+4})}{2}$
$= \dfrac{(k+4)\{14+(3-k)d\}}{2} = 11$
에서 $(k+4)\{14+(3-k)d\} = 22$
$k+4$는 $4$보다 큰 자연수이므로
$k+4 = 11$ 또는 $k+4 = 22$
즉, $k =7$ 또는 $k = 18$
$k =7$일 때, $14+(3-7)d = 2$에서 $d = 3$
$k =18$일 때, $14+(3-18)d = 1$에서 $d = \frac{13}{15}$
$d$는 자연수이므로 $d = 3$, $k = 7$
따라서 $a_{k+6} = a_{k+1} + 5d = 7 + 5 \times 3 = 22$
$48$
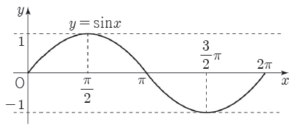 $\frac{1}{4}k = -\frac{1}{4}k^{2}+\frac{3}{4}k$에서 $k(k-2) = 0$
$\frac{1}{4}k = -\frac{1}{4}k^{2}+\frac{3}{4}k$에서 $k(k-2) = 0$
$k = 0$ 또는 $k = 2$
(ⅰ) $k = 0$ 또는 $k = 2$일 때
방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k ) = 0$의 서로 다른 해의 개수는 방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수와 같다.
방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수는 $k = 0$일 때 $3$이고 $k=2$일 때 $2$이다.
그러므로 방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k ) = 0$의 서로 다른 해의 개수가 $2$가 되도록 하는 $k$의 값은 $2$이다.
(ⅱ) $k \ne 0$이고 $k \ne 2$일 때
방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k) = 0$의 서로 다른 해의 개수는 방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수와 방정식 $\sin x = -\frac{1}{4}k^{2}+\frac{3}{4}k$의 서로 다른 해의 개수의 합과 같다.
(a) 방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수가 $0$일 때
$|\,k\,| \gt 4$이고, $|\,k\,| \gt 4$일 때 방정식 $\sin x = -\frac{1}{4}k^{2}+\frac{3}{4}k$의 서로 다른 해의 개수는 $0$이다.
그러므로 방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k) = 0$의 서로 다른 해의 개수는 $0$이다.
(b) 방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수가 $1$일 때
$|\,k\,| = 4$이므로 $k = 4$ 또는 $k = -4$
방정식 $\sin x = -\frac{1}{4}k^{2}+\frac{3}{4}k$의 서로 다른 해의 개수는 $k = 4$일 때 $1$이고 $k = -4$일 때 $0$이므로 방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k) = 0$의 서로 다른 해의 개수가 $2$가 되도록 하는 $k$의 값은 $4$이다.
(c) 방정식 $\sin x = \frac{1}{4}k$의 서로 다른 해의 개수가 $2$일 때
$|\,k\,| \lt 4$ $\cdots\cdots$ ㉠
방정식 $(\sin x-\frac{1}{4}k)(\sin x+\frac{1}{4}k^{2}-\frac{3}{4}k) = 0$의 서로 다른 해의 개수가 $2$가 되기 위해서는 방정식 $\sin x = -\frac{1}{4}k^{2}+\frac{3}{4}k$의 서로 다른 해의 개수가 $0$이어야 하므로 $k \lt -1$, $k \gt 4$ $\cdots\cdots$ ㉡
㉠, ㉡을 동시에 만족시키는 정수 $k$는 $-3$, $-2$
(ⅰ), (ⅱ)에 의하여 구하는 정수 $k$는 $-3$, $-2$, $2$, $4$이므로 모든 정수 $k$의 값의 곱은
$-3 \times (-2) \times 2 \times 4 = 48$
(가) 임의의 두 양수 $t_1$, $t_2$에 대하여
$t_{1} \lt t_{2}$이면 $h(t_{1}) \ge h(t_{2})$이다.
(나) 함수 $h(t)$는 $t = 0$, $t = \alpha$, $t = \beta$ ($0 \lt \alpha \lt \beta$)에서만 불연속이며 $h(0) = \alpha$, $h(\alpha) = \beta-1$이다.
$f(a-b)$의 값을 구하시오. [4점]
$75$
$y = \frac{bx}{x+a} = -\frac{ab}{x+a} + b$이므로
함수 $y = \frac{bx}{x+a}$의 그래프의 점근선은 $x = -a$, $y = b$
함수 $g(x)$는 $x = 1$에서 연속이므로
$g(1) = \displaystyle \lim_{x \to 1-}\frac{bx}{x+a} = \frac{b}{1+a} \lt b$
이차함수 $f(x)$의 꼭짓점의 $x$좌표를 $k$라 하자.
$k \le 1$일 때, 함수 $y = |\,g(x)\,|$의 그래프의 개형은 그림과 같다. 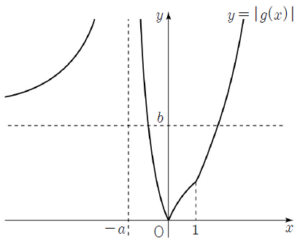 $0 \lt t \le b$인 $t$에 대하여 $h(t) = 2$이고
$0 \lt t \le b$인 $t$에 대하여 $h(t) = 2$이고
$t \gt b$인 $t$에 대하여 $h(t) = 3$이므로 조건 (가)를 만족시키지 않는다.
그러므로 $k \gt 1$
(ⅰ) $f(k) \gt -b$일 때
(a) $f(k) \ge -g(1)$일 때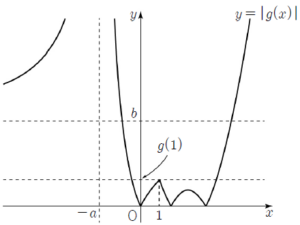 $|\,f(k)\,| \le g(1)$이므로 $g(1) \lt t \le b$인 $t$에 대하여 $h(t) = 2$이고
$|\,f(k)\,| \le g(1)$이므로 $g(1) \lt t \le b$인 $t$에 대하여 $h(t) = 2$이고
$t \gt b$인 $t$에 대하여 $h(t) = 3$이므로 조건 (가)를 만족시키지 않는다.
(b) $-b \lt f(k) \lt -g(1)$일 때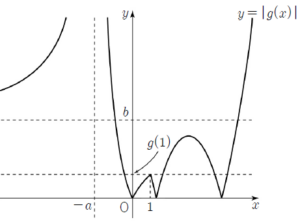 $g(1) \lt -f(k) \lt b$이므로
$g(1) \lt -f(k) \lt b$이므로
$-f(k) \lt t \le b$인 $t$에 대하여 $h(t) = 2$이고
$t \gt b$인 $t$에 대하여 $h(t) = 3$이므로 조건 (가)를 만족시키지 않는다.
(ⅱ) $f(k) = -b$일 때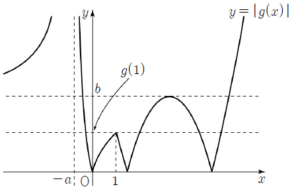 $t \lt 0$일 때, $h(t) = 0$
$t \lt 0$일 때, $h(t) = 0$
$t = 0$일 때, $h(0) = 3$
$0 \lt t \lt g(1)$일 때, $h(t) = 6$
$t = g(1)$일 때, $h(g(1)) = 5$
$g(1) \lt t \lt b$일 때, $h(t) = 4$
$t \ge b$일 때, $h(t) = 3$
그러므로
$h(t) = \begin{cases} 0 & (t \lt 0) \\ 3 & (t = 0, \,t \ge b) \\ 4 & (g(1) \lt t \lt b) \\ 5 & (t = g(1)) \\ 6 & (0 \lt t \lt g(1)) \end{cases}$
이며 함수 $h(t)$는 조건 (가)를만족시킨다.
함수 $h(t)$가 $t = 0$, $t = g(1)$, $t = b$에서만 불연속이므로 조건 (나)에 의하여
$\alpha = g(1)$, $\beta = b$
$g(1) = \alpha = h(0) = 3$이므로 $g(1) = \frac{b}{1+a} = 3$
$h(\alpha) = h(g(1)) = 5$이고
$h(\alpha) = \beta -1 = b-1$이므로 $b=6$, $a=1$
$f(k) = -6$이므로 $f(x) = (x-k)^{2}-6$
$f(1) = g(1) = 3$이므로 $(1-k)^{2}-6 = 3$에서 $k = 4$
그러므로 $f(x) = (x-4)^{2}-6$
(ⅲ) $f(k) \lt -b$일 때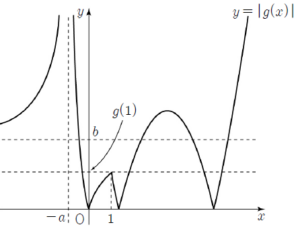 $-f(k) \gt b$이므로
$-f(k) \gt b$이므로
$g(1) \lt t \le b$인 $t$에 대하여 $h(t) = 4$이고
$b \lt t \lt -f(k)$인 $t$에 대하여 $h(t) = 5$이므로 조건 (가)를 만족시키지 않는다.
(ⅰ), (ⅱ), (ⅲ)에 의하여
$f(a-b) = f(1-6) = (-5-4)^{2}-6 = 75$