25년 10월 교육청
3. 첫째항이 $8$이고 공비가 $0$이 아닌 등비수열 $\{ a_n \}$이 $$a_{1}a_3 = 2 a_{2}a_4$$ 를 만족시킬 때, $a_5$의 값은? [3점]
① $\frac{1}{4}$
② $\frac{1}{2}$
③ $1$
④ $2$
⑤ $4$
4. 함수 $$\begin{cases} x^{2}+a & (x \lt 3) \\ x+2a & (x \ge 3) \end{cases}$$ 이 실수 전체의 집합에서 연속일 때, 상수 $a$의 값은? [3점]
① $6$
② $7$
③ $8$
④ $9$
⑤ $10$
6. $\pi \lt \theta \lt \frac{3}{2}\pi$인 $\theta$에 대하여 $\tan(\pi-\theta) = -2$일 때, $\cos \theta-\sin \theta$의 값은? [3점]
① $-\frac{\sqrt{5}}{5}$
② $-\frac{\sqrt{5}}{10}$
③ $0$
④ $\frac{\sqrt{5}}{10}$
⑤ $\frac{\sqrt{5}}{5}$
⑤
$\tan(\pi-\theta) = -\tan \theta = -2$에서 $\tan \theta = 2$
$\frac{\sin \theta}{\cos \theta} = 2$에서 $\sin \theta = 2 \cos \theta$
$\sin^{2}\theta + \cos^{2}\theta = 1$에서
$4\cos^{2}\theta + \cos^{2}\theta = 1$, $\cos^{2}\theta = \frac{1}{5}$
$\pi \lt \theta \lt \frac{3}{2}\pi$이므로 $\cos \theta \lt 0$, $\sin \theta \lt 0$
$\cos \theta = -\frac{\sqrt{5}}{5}$이므로 $\sin \theta = 2\cos \theta = -\frac{2\sqrt{5}}{5}$
따라서 $\cos \theta-\sin \theta = -\frac{\sqrt{5}}{5}-(-\frac{2\sqrt{5}}{5})$ $= \dfrac{\sqrt{5}}{5}$
9. 수직선 위를 움직이는 두 점 $\mathrm{P}$, $\mathrm{Q}$의 시각 $t$ ($t \ge 0$)에서의 위치가 각각 $$x_1 = -t^{3}+7t^{2}-10t, \: x_2 = t^{2}+2t$$ 이다. 두 점 $\mathrm{P}$, $\mathrm{Q}$의 속도가 같아지는 순간 두 점 $\mathrm{P}$, $\mathrm{Q}$사이의 거리는? [4점]
① $6$
② $7$
③ $8$
④ $8$
⑤ $10$
③
두 점 $\mathrm{P}$, $\mathrm{Q}$의 시각 $t$ ($t \ge 0$)에서의 속도를 각각 $v_1$, $v_2$라 하면
$v_1 = -3t^{2}+14t-10$, $v_2 = 2t_2$
두 점 $\mathrm{P}$, $\mathrm{Q}$의 속도가 같으므로
$-3t^{2}+14t-10 = 2t_2$
$3t^{2}-12t+12 = 0$
$3(t-2)^{2} = 0$
$t = 2$
두 점 $\mathrm{P}$, $\mathrm{Q}$의 시각 $t = 2$에서의 위치는 각각 $0$, $8$이므로 시각 $t = 2$에서 두 점 $\mathrm{P}$, $\mathrm{Q}$ 사이의 거리는 $8$
10. 두 양수 $a$, $b$에 대하여 닫힌구간 $[\,0, \,2a\,]$에서 정의된 함수 $$f(x) = 3 \sin \frac{\pi x}{a} + b$$ 의 그래프가 $x$축과 오직 한 점 $(2, 0)$에서 만날 때, $a+b$의 값은? [4점]
① $\frac{25}{6}$
② $\frac{13}{3}$
③ $\frac{9}{2}$
④ $\frac{14}{3}$
⑤ $\frac{29}{6}$
②
함수 $y = f(x)$의 그래프는 $y = 3 \sin \frac{\pi x}{a}$의 그래프를 $y$축의 방향으로 $b$ ($b \gt 0$) 만큼 평행이동한 것이고 함수 $y = f(x)$의 그래프가 $x$축과 오직 한 점에서 만나므로 함수 $f(x)$의 최솟값은 $0$이다. 함수 $f(x)$는 $x = \frac{3a}{2}$일 때, 최솟값 $0$을 가지므로 $\frac{3a}{2} = 2$, $a = \frac{4}{3}$이고
$f(\frac{3a}{2}) = -3+b = 0$, $b = 3$
따라서 $a+b = \frac{4}{3}+3 = \dfrac{13}{3}$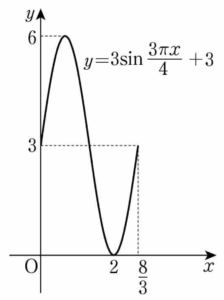 
11. 이차함수 $f(x)$가 모든 실수 $x$에 대하여 $$(x+3)f(x) = \int_{-3}^{x}(4f(t)-2t^{2})dt$$ 를 만족시킨다. $f(2)$의 값은? [4점]
① $24$
② $25$
③ $26$
④ $27$
⑤ $28$
③
$(x+3)f(x) = \int_{-3}^{x}(4f(t)-2t^{2})dt$의 양변을 $x$에 대하여 미분하면
$f(x)+(x+3)f'(x) = 4f(x)-2x^{2}$ $\cdots\cdots$ ㉠
$(x+3)f'(x) = 3f(x)-2x^{2}$
세 실수 $a$ ($a \ne 0$), $b$, $c$에 대하여
$f(x) = ax^{2}+bx+c$라 하면
$(x+3)f'(x) = (x+3)(2ax+b)$ $= 2ax^{2}+(6a+b)x+3b$
$3f(x)-2x^{2} = (3a-2)x^{2}+3bx+3c$
㉠에서 항등식의 성질에 의해 $a = 2$, $b = 6$, $c = 6$
따라서 $f(x) = 2x^{2}+6x+6$이므로 $f(2) = 26$
12. 모든 항이 정수이고 다음 조건을 만족시키는 모든 수열 $\{ a_n \}$에 대하여 $\displaystyle \sum_{n=1}^{30}a_n$의 최댓값과 최솟값을 각각 $M$, $m$이라 할 때, $M-m$의 값은? [4점]
모든 자연수 $n$에 대하여 $3a_{n}^{2}+2na_{n}-8n^{2} = 0$이다.
① $540$
② $550$
③ $560$
④ $570$
⑤ $580$
②
$3a_{n}^{2}+2na_{n}-8n^{2} = 0$에서 $(3a_{n}-4n)(a_{n}+2n) = 0$
$a_{n} = \frac{4}{3}n$ 또는 $a_{n} = -2n$
수열 $\{ a_n \}$의 모든 항이 정수이므로
자연수 $k$에 대하여
$a_{n} = \begin{cases} -6k+4 & (n=3k-2) \\ -6k+2 & (n=3k-1) \\ -6k \text{ 또는 } 4k & (n=3k) \end{cases}$
$-6k \lt 0$, $4k \gt 0$이므로 $1 \le k \le 10$인 모든 자연수 $k$에 대하여
$a_{3k} = 4k$일 때, $\displaystyle \sum_{n=1}^{30}a_n$은 최댓값 $M$을 갖고
$a_{3k} = -6k$일 때, $\displaystyle \sum_{n=1}^{30}a_n$은 최솟값 $m$을 갖는다.
$M = \displaystyle \sum_{n=1}^{30}a_n = \sum_{k=1}^{10}a_{3k-2} + \sum_{k=1}^{10}a_{3k-1} + \sum_{k=1}^{10}4k$이고,
$m = \displaystyle \sum_{n=1}^{30}a_n = \sum_{k=1}^{10}a_{3k-2} + \sum_{k=1}^{10}a_{3k-1} + \sum_{k=1}^{10}(-6k)$이므로
$M-m$ $ = \displaystyle \left( \sum_{k=1}^{10}a_{3k-2} + \sum_{k=1}^{10}a_{3k-1} + \sum_{k=1}^{10}4k \right)-\left( \sum_{k=1}^{10}a_{3k-2} + \sum_{k=1}^{10}a_{3k-1} + \sum_{k=1}^{10}(-6k) \right)$
$= \displaystyle \sum_{k=1}^{10}4k-\sum_{k=1}^{10}(-6k)$
$= \displaystyle \sum_{k=1}^{10}\{4k-(-6k)\}$
$= \displaystyle \sum_{k=1}^{10}10k$
$= \displaystyle 10\sum_{k=1}^{10}k$
$= 10 \times \dfrac{10 \times 11}{2} = 550$
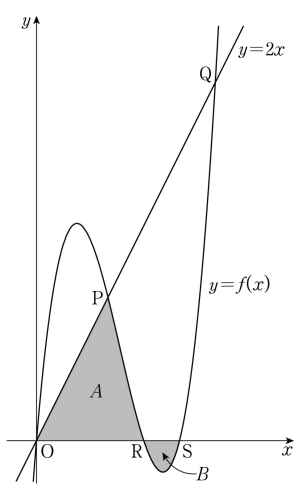
13. 상수 $a$ ($a \gt 1$)에 대하여 최고차항의 계수가 $1$인 삼차함수 $f(x)$가 $$f(0) = f(a) = f(a+1) = 0$$ 을 만족시킨다. 곡선 $y = f(x)$와 직선 $y = 2x$가 세 점 $\mathrm{O}$, $\mathrm{P}$, $\mathrm{Q}$ ($\overline{\mathrm{OP}} \lt \overline{\mathrm{OQ}}$)에서 만난다. 두 점 $\mathrm{R}(a, 0)$, $\mathrm{S}(a+1, 0)$에 대하여 곡선 $y = f(x)$와 두 선분 $\mathrm{OP}$, $\mathrm{OR}$로 둘러싸인 부분의 넓이를 $A$, 곡선 $y = f(x)$와 선분 $\mathrm{RS}$로 둘러싸인 부분의 넓이를 $B$라 하자. $\overline{\mathrm{OQ}} = 5\sqrt{5}$일 때, $A-B$의 값은? (단, $\mathrm{O}$는 원점이다.) [4점]
① $\frac{61}{12}$
② $\frac{31}{6}$
③ $\frac{21}{4}$
④ $\frac{16}{3}$
⑤ $\frac{65}{12}$
④
$f(x) = x(x-a)(x-a-1)$이므로
곡선 $y = f(x)$와 직선 $y = 2x$가 만나는 점의 $x$좌표는 $x(x-a)(x-a-1) = 2x$에서
$x(x-a+1)(x-a-2) = 0$
$x = 0$ 또는 $x = a-1$ 또는 $x = a+2$
$a \gt 1$, $\overline{\mathrm{OP}} \lt \overline{\mathrm{OQ}}$이므로 점 $\mathrm{P}$의 좌표는 $(a-1, 2a-2)$
$\mathrm{Q}$의 좌표는 $(a+2, 2a+4)$
$\overline{\mathrm{OQ}} = \sqrt{5(a+2)^{2}} = 5\sqrt{5}$이므로 $a = 3$
$\mathrm{P}(2, 4)$, $\mathrm{Q}(5, 10)$이고 $f(x) = x^{3}-7x^{2}+12x$
$A = \int_{0}^{2}2xdx+\int_{2}^{3}(x^{3}-7x^{2}+12x)dx$
$B = \int_{3}^{4}\{-(x^{3}-7x^{2}+12x)\}dx$
$A-B = \int_{0}^{2}2xdx+\int_{2}^{4}(x^{3}-7x^{2}+12x)dx$
$= \bigg[ x^{2}\bigg]_{0}^{2}+\bigg[ \dfrac{1}{4}x^{4}-\dfrac{7}{3}x^{3}+6x^{2}\bigg]_{2}^{4}$ $= \dfrac{16}{3}$
14. 그림과 같이 $\overline{\mathrm{BC}} = 6$인 삼각형 $\mathrm{ABC}$에서 선분 $\mathrm{AC}$를 $4 : 3$으로 내분하는 점을 $\mathrm{D}$라 하자. 선분 $\mathrm{BD}$ 위의 점 $\mathrm{E}$가 $\angle \mathrm{DAE} = \angle \mathrm{DBC}, \: \sin (\angle \mathrm{DAE}) : \sin (\angle \mathrm{EDA}) = 1 : 3$ 을 만족시킨다. $\overline{\mathrm{AE}} = \sqrt{5}$일 때, 삼각형 $\mathrm{BCD}$의 외접원의 넓이는? [4점]
① $\frac{180}{11}\pi$
② $\frac{195}{11}\pi$
③ $\frac{210}{11}\pi$
④ $\frac{225}{11}\pi$
⑤ $\frac{240}{11}\pi$
①
$\angle \mathrm{DAE} = \alpha$, $\angle \mathrm{EDA} = \beta$라 하자.
삼각형 $\mathrm{DAE}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{DE}}}{\sin \alpha} = \dfrac{\overline{\mathrm{AE}}}{\sin \beta}$이고,
$\sin \alpha : \sin \beta = 1 : 3$이므로 $\overline{\mathrm{DE}} : \overline{\mathrm{AE}} = 1 : 3$
$\overline{\mathrm{AE}} = \sqrt{5}$이므로 $\overline{\mathrm{DE}} = \frac{\sqrt{5}}{3}$
$\angle \mathrm{DBC} = \angle \mathrm{DAE} = \alpha$이므로 $\sin (\angle \mathrm{DBC}) = \sin \alpha$
$\sin (\angle \mathrm{CDB}) = \sin (\pi-\beta) = \sin \beta$
삼각형 $\mathrm{BCD}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{CD}}}{\sin (\angle \mathrm{DBC})} = \dfrac{\overline{\mathrm{BC}}}{\sin (\angle \mathrm{CDB})}$, $\dfrac{\overline{\mathrm{CD}}}{\sin \alpha} = \dfrac{\overline{\mathrm{BC}}}{\sin \beta}$이고,
$\sin \alpha : \sin \beta = 1 : 3$이므로 $\overline{\mathrm{CD}} : \overline{\mathrm{BC}} = 1 : 3$
$\overline{\mathrm{CD}} = \frac{1}{3}\overline{\mathrm{BC}} = \frac{1}{3}\times 6 = 2$
$\overline{\mathrm{AD}} : \overline{\mathrm{DC}} = 4 : 3$이므로 $\overline{\mathrm{AD}} = \frac{4}{3}\overline{\mathrm{DC}} = \frac{8}{3}$
삼각형 $\mathrm{ADE}$에서 코사인법칙에 의하여
$\overline{\mathrm{AE}}^{2} = \overline{\mathrm{DA}}^{2} + \overline{\mathrm{DE}}^{2}-2\times\overline{\mathrm{DA}}\times \overline{\mathrm{DE}} \times \cos (\angle \mathrm{EDA})$
$(\sqrt{5})^{2} = (\frac{8}{3})^{2} + (\frac{\sqrt{5}}{3})^{2}-2\times\frac{8}{3}\times \frac{\sqrt{5}}{3} \times \cos \beta$
$\cos \beta = \frac{8}{2\sqrt{5}}$
$\sin \beta = \sqrt{1-\cos^{2} \beta} = \sqrt{1-(\frac{8}{2\sqrt{5}})^{2}} = \frac{\sqrt{11}}{2\sqrt{5}}$
삼각형 $\mathrm{BCD}$의 외접원의 반지름의 길이를 $R$이라 하면 삼각형 $\mathrm{BCD}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{BC}}}{\sin (\angle \mathrm{CDB})} = 2R$, $\dfrac{6}{\sin \beta} = 2R$, $\dfrac{6}{\frac{\sqrt{11}}{2\sqrt{5}}} = 2R$
$R = \frac{6\sqrt{5}}{\sqrt{11}}$
따라서 삼각형 $\mathrm{BCD}$의 외접원의 넓이는 $\dfrac{180}{11}\pi$
15. 최고차항의 계수가 양수인 이차함수 $f(x)$에 대하여 함수 $g(x)$를 $$g(x) = \int_{0}^{x}|f(t)|dt+\bigg|\int_{0}^{x}f(t)dt\,\bigg|$$ 라 하자. 함수 $g(x)$가 다음 조건을 만족시킨다.
(가) $g(x) = 0$을 만족시키는 모든 실수 $x$의 값의 범위는 $-7 \le x \le 0$이다.
(나) 양수 $p$에 대하여 $g(x) = 81$을 만족시키는 모든 실수 $x$의 값의 범위는 $4p \le x \le 7p$이다.
$f(-10)$의 값은? [4점]
① $3$
② $6$
③ $9$
④ $12$
⑤ $15$
④
모든 실수 $x$에 대하여 $f(x) \ge 0$이면
$x \gt 0$일 때
$g(x) = \int_{0}^{x}f(t)dt + \int_{0}^{x}f(t)dt = 2\int_{0}^{x}f(t)dt$
$g'(x) = 2f(x) \ge 0$
함수 $g(x)$는 $x \gt 0$에서 증가하므로 (나)를 만족시키지 않는다.
그러므로 $f(x) = a(x-\alpha)(x-\beta)$를 만족시키는 세 실수 $a$, $\alpha$, $\beta$ ($a \gt 0$, $\alpha \lt \beta$)가 존재한다.
$\beta \le 0$이면 (나)를 만족시키지 않고, $\alpha \ge 0$이면 $x \le 0$에서 $g(x) = 0$이므로 (가)를 만족시키지 않는다.
그러므로 $\alpha \lt 0 \lt \beta$이고 $f(0) \lt 0$이므로
$\int_{0}^{\gamma}f(x)dx =m0$을 만족시키는 실수 $\gamma$ ($\beta \lt \gamma$)가 존재한다.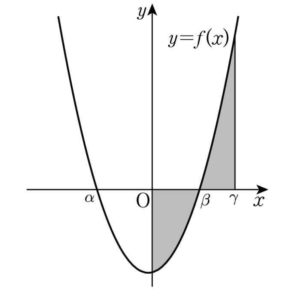
(ⅰ) $x \le 0$일 때
$\alpha \le x \le 0$인 $x$에 대하여
$g(x) = \int_{x}^{0}f(t)dt-\int_{x}^{0}f(t)dt = 0$ $\cdots\cdots$ ㉠
$x \lt \alpha$인 $x$에 대하여
$\int_{x}^{\alpha}f(t)dt \gt 0$, $\int_{\alpha}^{0}f(t)dt \lt 0$이므로
$g(x) = -\int_{x}^{\alpha}f(t)dt + \int_{\alpha}^{0}f(t)dt + |\,\int_{x}^{\alpha}f(t)dt + \int_{\alpha}^{0}f(t)dt\,|$ $\cdots\cdots$ ㉡
㉠, ㉡에 의해 $\alpha = -7$
(ⅱ) $x \gt 0$일 때
$0 \lt x \lt \beta$인 $x$에 대하여
$g(x) = -\int_{0}^{x}f(t)dt-\int_{0}^{x}f(t)dt = -2\int_{0}^{x}f(t)dt$
$g'(x) = -2f(x) \gt 0$
$g(x)$는 $0 \lt x \lt \beta$에서 증가한다. $\cdots\cdots$ ㉢
$\beta \le x \le \gamma$인 $x$에 대하여
$g(x) = -\int_{0}^{\beta}f(t)dt+\int_{\beta}^{x}f(t)dt-\int_{0}^{x}f(t)dt$ $= -\int_{0}^{\beta}f(t)dt$
$\beta \le x \le \gamma$에서 $g(x) = c$ ($c$는 상수) $\cdots\cdots$ ㉣
$x \gt \gamma$인 $$x에 대하여
$g(x) = -\int_{0}^{\beta}f(t)dt + \int_{\beta}^{x}f(t)dt + |\,\int_{0}^{\gamma}f(t)dt + \int_{\gamma}^{x}f(t)dt\,|$
$= -\int_{0}^{\beta}f(t)dt + \int_{\beta}^{x}f(t)dt + \int_{\gamma}^{x}f(t)dt$
$= -2\int_{0}^{\beta}f(t)dt + 2\int_{\gamma}^{x}f(t)dt$
$g'(x) = 2f(x) \gt 0$
$g(x)$는 $x \gt \gamma$에서 증가한다. $\cdots\cdots$ ㉤
㉢, ㉣, ㉤에 의해 $\beta = 4p$, $\gamma = 7p$
$-2\int_{0}^{\beta}f(t)dt = -2\int_{0}^{4p}f(t)dt = 81$이다.
(ⅰ), (ⅱ)에 의해
$f(x) = a(x+7)(x-4p) = a\{x^{2}+(7-4p)x-28p \}$
$\int_{0}^{\gamma}f(x)dx = \int_{0}^{7p}f(x)dx = \frac{49}{6}ap^{2}(2p-3) = 0$
$a \gt 0$, $p \gt 0$이므로 $p = \frac{3}{2}$, $\beta = 6$
$f(x) = a(x+7)(x-6) = a(x^{2}+x-42)$
$\int_{0}^{\beta}f(x)dx = \int_{0}^{6}a(x^{2}+x-42)dx = -162a = -\frac{81}{2}$
이므로 $a = \frac{1}{4}$
따라서 $f(x) = \frac{1}{4}(x+7)(x-6)$이므로 $f(-10) = 12$
16. 방정식 $$\log_{4}(x+2) + \log_{4}2 = \log_{2}(x-2)$$ 를 만족시키는 실수 $x$의 값을 구하시오. [3점]
18. 두 수열 $\{ a_n \}$, $\{ b_n \}$에 대하여 $$\sum_{n=1}^{7}(a_{n}-2)(b_{n}-2) = 60, \:\sum_{n=1}^{7}(a_{n}+b_{n}) = 44$$ 일 때, $\displaystyle \sum_{n=1}^{7}a_{n}b_n$의 값을 구하시오. [3점]
19. 두 상수 $a$, $b$에 대하여 함수 $f(x)$를 $$f(x) = x^{3}-6x^{2}+ax+b$$ 라 하자. 함수 $f(x)$는 $x = 3$에서 극값을 갖고, 함수 $f(x)$의 극댓값과 극솟값의 합이 $8$이다. $a+b$의 값을 구하시오. [3점]
20. 상수 $a$에 대하여 실수 전체의 집합에서 최솟값을 갖는 함수 $$f(x) = \begin{cases} 2^{x+7}+7 & (x \lt -2) \\ -\left( \dfrac{1}{2} \right)^{x-a} & (x \ge -2) \end{cases}$$ 가 있다. 실수 $t$에 대하여 함수 $y = f(x)$의 그래프와 직선 $x+2^{a}y-t=0$이 만나는 점의 개수를 $g(t)$라 하자. $g(t) = 2$를 만족시키는 $t$의 최솟값이 함수 $f(x)$의 최솟값과 같도록 하는 모든 $2^{a}$의 값의 곱을 구하시오. [4점]
$3$
$x \lt -2$에서 함수 $y = 2^{x+2}+7$의 치역은 $\{ y \,|\, 7 \lt y \lt 8 \}$이고, $x \ge -2$에서 함수 $y = -(\frac{1}{2})^{x-a}+10$의 치역은 $\{ y \,|\, -2^{a+2} \le y \lt 10 \}$이다.
함수 $f(x)$의 최솟값이 존재하기 위해서는
$-2^{a+2}+10 \le 7$
$2^{a} \ge \frac{3}{4}$ $\cdots\cdots$ ㉠
함수 $f(x)$의 최솟값은 $-2^{a+2}+10$ $\cdots\cdots$ ㉡
직선 $x+2^{a}y-t = 0$은 점 $(t, 0)$을 지나므로 $t$는 이 직선의 $x$절편이다.
점 $(-2, 8)$을 지나는 직선 $x+2^{a}y-t = 0$의 $x$절편은
$t = -2+2^{a}\times 8 = 2^{a+3}-2$
점 $(-2, -2^{a+2}+10)$을 지나는 직선 $x+2^{a}y-t = 0$의 $x$절편은
$t = -2+2^{a}\times (-2^{a+2}+10) = -2^{2a+2}+10\times 2^{a}-2$
$g(t) = 2$를 만족시키는 실수 $t$의 값의 범위는
$-2^{2a+2}+10\times 2^{a}-2 \le t \lt 2^{a+3}-2$
$t$의 최솟값은 $-2^{2a+2}+10\times 2^{a}-2$ $\cdots\cdots$ ㉢
㉡, ㉢에서
$-2^{2a+2}+10 = -2^{2a+2}+10\times 2^{a}-2$
$4 \times (2^{a})^{2}-14\times 2^{a}+12 = 0$
$2(2\times 2^{a}-3)(2^{a}-2) = 0$
㉠에서 $2^{a} \ge \frac{3}{4}$이므로 $2^{a} = \frac{3}{2}$ 또는 $2^{a} = 2$
따라서 모든 $2^{a}$의 값의 곱은 $\frac{3}{2} \times 2 = 3$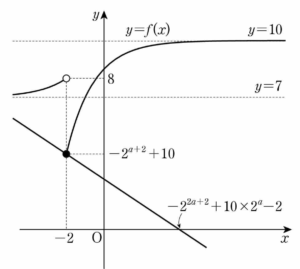 
21. 최고차항의 계수가 $1$인 사차함수 $f(x)$가 다음 조건을 만족시킨다.
$\displaystyle \lim_{x \to k}\frac{2x^{2}f(x)-(f(k))^{2}}{x-k} = \lim_{x \to k}\frac{(f(x))^{2}-(f(k))^{2}}{x-k}$을 만족시키는 실수 $k$는 $t$, $-t$ ($t \gt 1$)뿐이다.
함수 $f(x)$의 최솟값이 $17$일 때, $f(4)$의 값을 구하시오. [4점]
$81$
$\displaystyle \lim_{x \to k}\frac{(f(x))^{2}-(f(k))^{2}}{x-k}$
$= \displaystyle \lim_{x \to k} \left\{ (f(x)+f(k)) \times \frac{f(x)-f(k)}{x-k} \right\}$
$= 2f(k)f'(k)$
이므로 $\displaystyle \lim_{x \to k}\frac{2x^{2}f(x)-(f(k))^{2}}{x-k}$의 값이 존재한다.
$\displaystyle \lim_{x \to k}(x-k) = 0$이므로 $\displaystyle \lim_{x \to k}\{2x^{2}f(x)-(f(k))^{2} \} = 0$
$2k^{2}f(k)-(f(k))^{2} = 0$, $f(k)\{2k^{2}-(f(k))\} = 0$
이므로 $f(k) = 0$ 또는 $f(k) = 2k^{2}$
함수 $f(x)$의 최솟값이 $17$이므로 $f(k) = 2k^{2}$
$\displaystyle \lim_{x \to k}\frac{(f(x))^{2}-(f(k))^{2}}{x-k} = 4k^{2}f'(k)$
$\displaystyle \lim_{x \to k}\frac{2x^{2}f(x)-(f(k))^{2}}{x-k}$
$= \displaystyle \lim_{x \to k}\frac{2x^{2}f(x)-2k^{2}f(k)}{x-k}$
$= \displaystyle \lim_{x \to k} \bigg(2x^{2}\times \frac{f(x)-f(k)}{x-k} + f(k) \times \frac{2x^{2}-2k^{2}}{x-k} \bigg)$
$= 2k^{2}f'(k)+4kf(k)$
$= 2k^{2}f'(k)+8k^3$
$2k^{2}f'(k)+8k^{3} = 4k^{2}f'(k)$
$2k^{2}(f'(k)-4k) = 0$
$k \ne 0$이므로 $f'(k) = 4k$
$k = t$일 때, $f(t) = 2t^{2}$, $f'(t) = 4t$
$k = -t$일 때, $f(-t) = 2t^{2}$, $f'(-t) = -4t$
$f(t) = 2t^{2}$, $f(-t) = 2t^{2}$이므로
두 실수 $a$, $b$에 대하여
$f(x)-2t^{2} = (x-t)(x+t)(x^{2}+ax+b)$ $= (x^{2}-t^{2})(x^{2}+ax+b)$
$f'(x) = 2x(x^{2}+ax+b)+(x^{2}-t^{2})(2x+a)$
$f'(t) = 4t$, $f'(-t) = -4t$이므로
$f'(t) = 2t(t^{2}+at+b) = 4t$, $f'(-t) = -2t(t^{2}-at+b) = -4t$
$t \gt 1$이므로 $t^{2}+at+b = 2$, $t^{2}-at+b = 2$
에서 $a = 0$, $b = -t^{2}+2$
그러므로
$f(x) = (x^{2}-t^2)(x^{2}-t^{2}+2)+2t^2$ $= (x^{2}-t^{2}+1)^{2}+2t^{2}-1$
함수 $f(x)$의 최솟값은 $2t^{2}-1$이다.
$2t^{2}-1 =17$, $t = 3$
따라서 $f(x) = (x^{2}-8)^{2}+17$이므로 $f(4) = 81$
22. 실수 $k$에 대하여 다음 조건을 만족시키는 수열 $\{ a_n \}$이 있다.
$a_{1} = 3$이고, 모든 자연수 $n$에 대하여 $$a_{n+1} = \begin{cases} \: |\,a_{n} + n\,| & (a_{n} \lt 0) \\ \: a_{n}-10+k & (a_{n} \ge 0) \end{cases}$$ 이다.
$a_{4} \times a_{5} = 0$이 되도록 하는 $k$의 최댓값을 $M$, 최솟값을 $m$이라 할 때, $M+m = \dfrac{q}{p}$이다. $p + q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$63$
$a_{1} = 3$이므로 $a_{2} = a_{1}-10+k = k-7$
(ⅰ) $a_{2} \lt 0$인 경우, $k-7 \lt 0$에서 $k \lt 7$
$a_{3} = |a_{2}+2| = |k-5|$
$a_{3} \ge 0$이므로 $a_{4} = a_{3}-10+k = |k-5|-10+k$
① $k \lt 5$일 때
$a_{4} = -(k-5)-10+k = -5$
$a_{5} = |a_{4}+4| = 1$이므로
$a_{4}\times a_{5} = 0$을 만족하는 $k$의 값은 존재하지 않는다.
② $5 \le k \lt 7$일 때
$a_{4} = (k-5)-10+k = 2k-15$에서
$-5 \le 2k-15 \lt -1$
$a_{4} \ne 0$이므로 $a_{5} = 0$이어야 한다.
$|2k-11| = 0$에서 $k = \frac{11}{2}$
(ⅱ) $a_{2} \ge 0$인 경우, $k-7 \ge 0$에서 $k \ge 7$
$a_{3} = a_{2}-10+k = 2k-17$
① $7 \le k \lt \frac{17}{2}$일 때
$a_{3} \lt 0$이므로
$a_{4} = |a_{3}+3| = |(2k-17)+3| = 2k-14$
$a_{4} \ge 0$이므로
$a_{5} = a_{4}-10+k = (2k-14)-10+k = 3k-24$
$a_{4}\times a_{5} = (2k-14)(3k-24) = 0$이어야 하므로
$k=7$ 또는 $k=8$
② $k \ge \frac{17}{2}$일 때
$a_{3} \ge 0$이므로
$a_{4} = a_{3}-10+k = (2k-17)-10+k = 3k-27$
$\frac{17}{2} \le k \lt 9$일 때, $a_{4} \lt 0$이므로
$a_{5} = |a_{4}+4| = |(3k-27)+4| = 3k-23$이고,
$\frac{5}{2} \le a_{5} \lt 4$
그러므로 $a_{4}\times a_{5} = 0$을 만족하는 $k$의 값은 존재하지 않는다.
$k \ge 9$일 때, $a_{4} \ge 0$이므로
$a_{5} = a_{4}-10+k = (3k-27)-10+k = 4k-37$
$a_{4}\times a_{5} = (3k-27)(4k-37) = 0$이어야 하므로
$k = 9$ 또는 $k = \frac{37}{4}$
(ⅰ), (ⅱ)에서 구하는 모든 $k$의 값은 $\frac{11}{2}$, $7$, $8$, $9$, $\frac{37}{4}$이므로
$M = \frac{37}{4}$, $m = \frac{11}{2}$에서 $M+m = \frac{59}{4}$
따라서 $p = 4$, $q = 59$이므로 $p+q = 63$
수학 영역(확률과 통계)
24. 두 사건 $A$와 $B$는 서로 배반사건이고 $$\mathrm{P}(A \cup B) = \frac{1}{3}, \:\mathrm{P}(A^{c}) = \mathrm{P}(A)+\frac{1}{2}$$ 일 때, $\mathrm{P}(B)$의 값은? [3점]
① $\frac{1}{36}$
② $\frac{1}{18}$
③ $\frac{1}{12}$
④ $\frac{1}{9}$
⑤ $\frac{5}{36}$
③
$\mathrm{P}(A^{c}) = 1-\mathrm{P}(A)$에서 $1-\mathrm{P}(A) = \mathrm{P}(A) + \frac{1}{2}$, $\mathrm{P}(A) = \frac{1}{4}$
두 사건 $A$, $B$가 서로 배반사건이므로
$\mathrm{P}(A \cup B) = \mathrm{P}(A) + \mathrm{P}(B) = \frac{1}{4} +\mathrm{P}(B) = \frac{1}{3}$
따라서 $\mathrm{P}(B) = \frac{1}{3}-\frac{1}{4}$ $= \dfrac{1}{12}$
25. 한 개의 주사위를 두 번 던져서 나오는 눈의 수를 차례로 $a$, $b$라 할 때, $|\,a-b\,| = 1$일 확률은? [3점]
① $\frac{1}{6}$
② $\frac{7}{36}$
③ $\frac{2}{9}$
④ $\frac{1}{4}$
⑤ $\frac{5}{18}$
26. 어느 농장에서 수확하는 딸기 $1$개의 무게는 평균이 $m$, 표준편차가 $\sigma$인 정규분포를 따른다고 한다.
이 농장에서 수확하는 딸기 중에서 $100$개를 임의추출하여 얻은 표본평균을 이용하여 구한 $m$에 대한 신뢰도 $95$%의 신뢰구간이 $80a \le m \le 82a$이다.
이 농장에서 수확하는 딸기 중에서 $25$개를 임의추출하여 얻은 표본평균을 이용하여 구한 $m$에 대한 신뢰도 $95$%의 신뢰구간이 $78a \le m \le 80a + 0.49$이다. $\sigma$의 값은?
(단, 무게의 단위는 $\rm{g}$이고, $Z$가 표준정규분포를 따르는 확률변수일 때, $\mathrm{P}(|Z| \le 1.96) = 0.95$로 계산한다.) [3점]
① $\frac{1}{2}$
② $\frac{3}{4}$
③ $1$
④ $\frac{5}{4}$
⑤ $\frac{3}{2}$
④
이 농장에서 수확하는 딸기 중에서 $100$개를 임의추출하여 얻은 표본평균을 $\overline{x_1}$이라 하면 $m$에 대한 신뢰도 $95$%의 신뢰구간은
$\overline{x_1}-1.96 \times \frac{\sigma}{\sqrt{100}} \le m \le \overline{x_1}+1.96 \times \frac{\sigma}{\sqrt{100}}$
즉, $82a-80a = 2 \times 1.96 \times \frac{\sigma}{\sqrt{100}}$
$2a = 2 \times 1.96 \times \frac{\sigma}{10}$ $\cdots\cdots$ ㉠
이 농장에서 수확하는 딸기 중에서 $25$개를 임의추출하여 얻은 표본평균을 $\overline{x_2}$라 하면 $m$에 대한 신뢰도 $95$%의 신뢰구간은
$\overline{x_2}-1.96 \times \frac{\sigma}{\sqrt{25}} \le m \le \overline{x_2}+1.96 \times \frac{\sigma}{\sqrt{25}}$
즉, $(80a+0.49)-78a = 2 \times 1.96 \times \frac{\sigma}{\sqrt{25}}$
$2a + 0.49 = 2 \times 1.96 \times \frac{\sigma}{5}$ $\cdots\cdots$ ㉡
㉠, ㉡에서 $0.49 = 2 \times 1.96 \times \frac{\sigma}{10}$, $\sigma = \dfrac{5}{4}$
27. 다음 조건을 만족시키는 자연수 $a$, $b$, $c$의 모든 순서쌍 $(a, b, c)$의 개수는? [3점]
(가) $a\times b\times c = 144$
(나) $a$는 짝수이다.
① $60$
② $72$
③ $84$
④ $96$
⑤ $108$
①
조건 (가)에서 $144 = 2^{4}\times 3^2$이므로 자연수 $a$, $b$, $c$를 $a = 2^{x_1}\times 3^{y_1}$, $b = 2^{x_2}\times 3^{y_2}$, $c = 2^{x_3}\times 3^{y_3}$이라 하면
$a\times b\times c = 2^{x_{1}+x_{2}+x_{3}}\times 3^{y_{1}+y_{2}+y_{3}} = 2^{4}\times 3^2$에서 $x_{1}+x_{2}+x_{3} = 4$, $y_{1}+y_{2}+y_{3} = 2$이다.
조건 (나)에서 $x_{1} \ge 1$이므로 $x_{1}’ = x_{1}-1 \ge 0$이라 하면 $x_{1}’+x_{2}+x_{3} = 3$이다.
$x_{1}’+x_{2}+x_{3} = 3$의 음이 아닌 정수해의 개수는 ${}_{3}\rm{H}_{3} = {}_{5}\rm{C}_{3} = 10$
$y_{1}+y_{2}+y_{3} = 2$의 음이 아닌 정수해의 개수는 ${}_{3}\rm{H}_{2} = {}_{4}\rm{C}_{2} = 6$
따라서 구하는 순서쌍의 개수는 $10 \times 6 = 60$
28. 확률변수 $X$가 평균이 $m$이고, 표준편차가 $\dfrac{1}{2m}$인 정규분포를 따른다. 음수 $a$에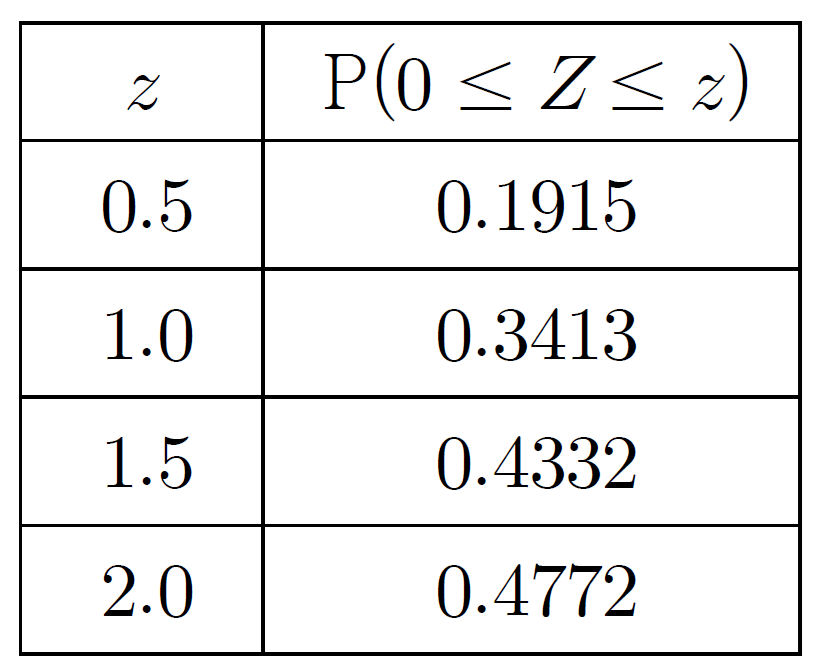
대하여
$$\mathrm{P}(X \le a)+\mathrm{P}(X \le a^2) = 1,$$ $$\:\mathrm{P}(X \le a^{2}+a) = 0.9772$$
일 때, $\mathrm{P}(X \le -\frac{a}{8})$의 값을 오른쪽 표준정규분포표를 이용하여 구한 것은? (단, $m \ne 0$) [4점]
① $0.9228$
② $0.0668$
③ $0,1587$
④ $0.1915$
⑤ $0.3085$
②
확률변수 $X$의 확률밀도함수를 $f(x)$라 하면 곡선 $y = f(x)$는 직선 $x = m$에 대하여 대칭이다.
$\mathrm{P}(X \le a)+\mathrm{P}(X \le a^2) = 1$에서 $a^{2} + a = 2m$
$\mathrm{P}(X \le a^{2}+a) = \mathrm{P}(X \le 2m)$
$= \mathrm{P}(Z \le \frac{2m-m}{\frac{2}{2m}}) = \mathrm{P}(Z \le 2m^2 ) =0.9772$
$\mathrm{P}(Z \le 2) =0.9772$이므로 $2m^{2} = 2$
표준편차 $\frac{1}{2m}$은 양수이므로 $m = 1$
$a^{2}+a = 2$, $(a+2)(a-1) = 0$에서 $a \lt 0$이므로 $a = -2$
$\mathrm{P}(X \le -\frac{a}{8}) = \mathrm{P}(X \le \frac{1}{4})$ $= \mathrm{P}(Z \le \frac{\frac{1}{4}-1}{\frac{1}{2}}) = \mathrm{P}(Z \le -1.5)$
$= 0.5-\mathrm{P}(-1.5 \le Z \le 0)$ $= 0.5-\mathrm{P}(0 \le Z \le 1.5)$
$= 0.5-0.4332 = 0.0668$
29. 집합 $X=\{ 2, 3, 5, 7, 11 \}$과 함수 $f : X \longrightarrow X$에 대하여 함수 $f$의 치역을 $A$, 합성함수 $f \circ f$의 치역을 $B$라 할 때, 다음 조건을 만족시키는 함수 $f$의 개수를 구하시오. [4점]
(가) $n(B) = 2$
(나) 집합 $A$의 모든 원소의 곱은 집합 $B$의 모든 원소의 곱의 $2$ 배이다.
$180$
합성함수 $f \circ f$의 치역은 함수 $f$의 치역의 부분집합이므로 $B \subset A$이고, 조건 (나)에서 $A-B = \{ 2 \}$이다.
$n(A) = n(B) + 1$이므로 조건 (가)에서 $n(A) = 2 + 1 = 3$
$A = \{ 2, a, b \}$, $B = \{ a, b \}$, $X-A = \{ c, d \}$라 하자.
두 수 $a$, $b$를 택하는 경우의 수는 ${}_{4}\rm{C}_{2} = 6$
$\{ f(2), f(a), f(b) \} = \{ a, b \}$이므로 $f(2)$, $f(a)$, $f(b)$의 값을 정하는 경우의 수는
${}_{2}\Pi_{3}-2 = 2^{3}-2 = 6$
$\{ f(c), f(d) \} \subset \{ 2, a, b \}$이고 $f(c) = 2$ 또는 $f(d) = 2$가 되도록 $f(c)$, $f(d)$의 값을 정하는 경우의 수는
${}_{3}\Pi_{2}-{}_{2}\Pi_{2} = 3^{2}-2^{2} = 5$
따라서 구하는 함수 $f$의 개수는 $6\times 6\times 5 = 180$
30. 두 상자 $\mathrm{A}$, $\mathrm{B}$에 각각 $8$개의 공이 들어 있다. 두 상자 $\mathrm{A}$, $\mathrm{B}$와 한 개의 주사위를 사용하여 다음 시행을 한다.
주사위를 한 번 던져
나온 눈의 수가 $3$의 배수이면
상자 $\mathrm{A}$에서 $2$개의 공을 꺼내어 상자 $\mathrm{B}$에 넣고,
나온 눈의 수가 $3$의 배수가 아니면
상자 $\mathrm{B}$에서 $1$개의 공을 꺼내어 상자 $\mathrm{A}$에 넣는다.
이 시행을 $4$번 반복한 후 상자 $\mathrm{A}$에 들어 있는 공의 개수가 상자 $\mathrm{B}$에 들어 있는 공의 개수보다 많을 때, 주사위의 짝수의 눈이 $4$번 나왔을 확률은 $\dfrac{q}{p}$이다. $p+q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$17$
시행을 $4$번 반복한 후 상자 $\mathrm{A}$에 들어 있는 공의 개수가 상자 $\mathrm{B}$에 들어 있는 공의 개수보다 많은 사건을 $X$, 주사위의 짝수의 눈이 $4$번 나오는 사건을 $Y$라 하자. $4$번의 시행에서 $3$의 배수의 눈이 $n$번 나왔을 때, 상자 $\mathrm{A}$에 들어 있는 공의 개수는
$8-2n+(4-n) = 12-3n$
상자 $\mathrm{B}$에 들어 있는 공의 개수는
$8+2n-(4-n) = 4+3n$
(ⅰ) 상자 $\mathrm{A}$에 들어 있는 공의 개수가 상자 $\mathrm{A}$에 들어 있는 공의 개수보다 많은 경우
$12-3n \gt 4+3n$에서 $n = 0$ 또는 $n = 1$
주사위를 한 번 던질 때 $3$의 배수의 눈이 나올 확률이 $\frac{1}{3}$이므로
$n = 0$일 확률은 ${}_{4}\rm{C}_{0}(\frac{1}{3})^{0}(\frac{2}{3})^{4} = \frac{16}{81}$
$n = 1$일 확률은 ${}_{4}\rm{C}_{1}(\frac{1}{3})^{1}(\frac{2}{3})^{3} = \frac{32}{81}$
그러므로 $\mathrm{P}(X) = \frac{16}{81} + \frac{32}{81} = \frac{16}{27}$
(ⅱ) 상자 $\mathrm{A}$에 들어 있는 공의 개수가 상자 $\mathrm{A}$에 들어 있는 공의 개수보다 많고 주사위의 짝수의 눈이 $4$번 나오는 경우
$n = 0$이면서 주사위의 짝수의 눈이 $4$번 나오는 경우는 $2$ 또는 $4$의 눈이 $4$번 나오는 경우이므로 구하는 확률은 $(\frac{1}{3})^{4} = \frac{1}{81}$
$n = 1$이면서 주사위의 짝수의 눈이 $4$번 나오는 경우는 $6$의 눈이 $1$번, $2$ 또는 $4$의 눈이 $3$번 나오는 경우이므로 구하는 확률은
$4 \times (\frac{1}{6}) \times (\frac{1}{3})^{3} = \frac{2}{81}$
그러므로 $\mathrm{P}(X \cap Y) = \frac{1}{81}+\frac{2}{81} = \frac{1}{27}$
(ⅰ), (ⅱ)에서 구하는 확률은
$\mathrm{P}(Y | X) = \dfrac{\mathrm{P}(X \cap Y)}{\mathrm{P}(X)}$ $= \dfrac{\frac{1}{27}}{\frac{16}{27}} = \dfrac{1}{16}$
따라서 $p = 16$, $q = 1$이므로 $p+q = 17$
수학 영역(미적분)
24. $\displaystyle \lim_{n \to \infty}\sum_{k=1}^{n}\frac{1}{2n+k}$의 값은? [3점]
① $\ln \frac{3}{2}$
② $\ln 2$
③ $\ln \frac{5}{2}$
④ $\ln 3$
⑤ $\ln \frac{7}{2}$
25. 등차수열 $\{ a_n \}$에 대하여 $\displaystyle \lim_{n \to \infty}(\sqrt{a_{n}^{\:2}+2n}-a_n)=\frac{1}{3}$일 때, 수열 $\{ a_n \}$의 공차는? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
③
등차수열 $\{ a_n \}$의 공차를 $d$라 하자.
$a_{n} = a_{1}+(n-1)d$에서 $\displaystyle \lim_{n \to \infty}\frac{a_n}{n} = \lim_{n \to \infty}\frac{a_{1}+(n-1)d}{n} = d$
$\displaystyle \lim_{n \to \infty}(\sqrt{a_{n}^{\:2}+2n}-a_n)= \lim_{n \to \infty}\frac{2n}{\sqrt{a_{n}^{\:2}+2n}+a_n}$
$= \displaystyle \lim_{n \to \infty}\frac{2}{\sqrt{(\frac{a_{n}}{n})^{2}+\frac{2}{n}}+\frac{a_n}{n}} = \frac{1}{3}$
이므로 $d \gt 0$
즉, $\displaystyle \lim_{n \to \infty}(\sqrt{a_{n}^{\:2}+2n}-a_n)=\frac{1}{d} =\frac{1}{3}$이므로 $d = 3$
26. 그림과 같이 곡선 $y = 2\sqrt{x}e^{-x^{2}}$과 $x$축 및 두 직선 $x = \dfrac{1}{2}$, $x = 1$로 둘러싸인 부분을 밑면으로 하는 입체도형이 있다. 이 입체도형을 $x$축에 수직인 평면으로 자른 단면이 모두 정사각형일 때, 이 입체도형의 부피는? [3점]
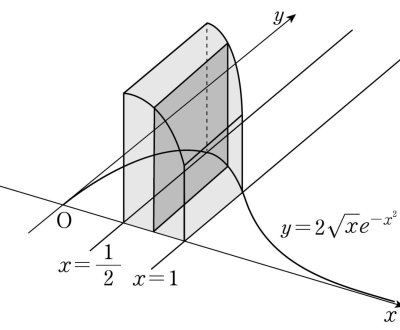
① $e^{-1}-e^{-2}$
② $e^{-\frac{1}{2}}-e^{-1}$
③ $e^{-\frac{1}{2}}-2e^{-2}$
④ $e^{-\frac{1}{2}}-e^{-2}$
⑤ $2e^{-\frac{1}{2}}-e^{-2}$
④
직선 $x = t$ ($\frac{1}{2} \le t \le 1$)을 포함하고 $x$축에 수직인 평면으로 입체도형을 자른 단면의 넓이를 $S(t)$라 하면
$S(t) = (2\sqrt{t}e^{-t^{2}})^{2} = 4te^{-2t^{2}}$
따라서 구하는 부피는 $\int_{\frac{1}{2}}^{1}S(t)dt = \int_{\frac{1}{2}}^{1}4te^{-2t^{2}}dt$
$-2t^{2} = s$로 놓으면 $-4t = \frac{ds}{dt}$이고
$t =\frac{1}{2}$일 때 $s=-\frac{1}{2}$, $t = 1$일 때 $s = -2$이므로
$\int_{\frac{1}{2}}^{1}S(t)dt = \int_{-\frac{1}{2}}^{-2}(-e^{s})ds$ $= \bigg[ -e^{s}\bigg]_{-\frac{1}{2}}^{-2}$ $= e^{-\frac{1}{2}}-e^{-2}$
27. 세 실수 $k$ ($k \lt -1$), $a$, $b$ ($1 \lt a \lt b$)에 대하여 두 점 $\mathrm{A}(a, b)$, $\mathrm{B}(b, a)$가 곡선 $C : x^{2}-xy+y^{2} + k = 0$ 위에 있다.
곡선 $C$ 위의 점 $\mathrm{A}$에서의 접선과 곡선 $C$ 위의 점 에서의 접선이 이루는 예각의 크기를 $\theta$라 하자.
$$\overline{\mathrm{AB}} = 2\sqrt{2}, \: \tan \theta = \frac{4}{3}$$
일 때, $k+a+b$의 값은? [3점]
① $-35$
② $-27$
③ $-19$
④ $-11$
⑤ $-3$
②
$\overline{\mathrm{AB}}^{2} = 2(a-b)^{2}$에서 $\overline{\mathrm{AB}} = \sqrt{2} \times |a-b| = 2\sqrt{2}$
$1 \lt a \lt b$이므로 $b-a = 2$ $\cdots\cdots$ ㉠
$x^{2}-xy+y^{2}+k = 0$의 양변을 $x$에 대하여 미분하면
$2x-y-x\frac{dy}{dx}+2y\frac{dy}{dx} = 0$
$\frac{dy}{dx} = \frac{2x-y}{x-2y}$ (단, $x \ne 2y$) $\cdots\cdots$ ㉡
곡선 $C$ 위의 두 점 $\mathrm{A}$, $\mathrm{B}$에서의 접선의 기울기를 각각 $m_1$, $m_2$라 하자.
㉡에 $x=a$, $x=b$를 대입하면 $m_1 = \frac{2a-b}{a-2b}$
㉠에서 $m_1 = \frac{2a-b}{a-2b} = \frac{a-2}{-a-4} = \frac{6}{a+4} = 1$
$a \gt 1$이므로 $-1 \lt m_1 \lt \frac{1}{5}$ $\cdots\cdots$ ㉢
㉡에 $x=b$, $y=a$를 대입하면 $m_2 = \frac{2b-a}{b-2a} = \frac{1}{m_1}$
$\tan \theta = |\frac{m_{1}-m_{2}}{1+m_{1}\times m_{2}}| = |\frac{m_{1}-\frac{1}{m_1}}{2}| = |\frac{m_{1}^{2}-1}{2m_{1}}|$ $= \frac{4}{3}$
(ⅰ) $\frac{m_{1}^{2}-1}{2m_{1}} = -\frac{4}{3}$인 경우
$3m_{1}^{2}+8m_{1}-3 = 0$에서 $m_{1} = -3$ 또는 $m_{1} = \frac{1}{3}$
이는 ㉢을 만족시키지 못한다.
(ⅱ) $\frac{m_{1}^{2}-1}{2m_{1}} = \frac{4}{3}$인 경우
$3m_{1}^{2}-8m_{1}-3 = 0$에서 $m_{1} = -\frac{1}{3}$ 또는 $m_{1} = 3$
㉢에서 $m_{1} = -\frac{1}{3}$
(ⅰ), (ⅱ)에서 $m_{1} = \frac{6}{a+4}-1 = -\frac{1}{3}$, $a=5$
㉠에서 $b=7$이고 곡선 $C$가 점 $\mathrm{A}(5, 7)$을 지나므로
$5^{2}-5\times 7+7^{2}+k = 0$, $k = -39$
따라서 $k+a+b = (-39)+5+7 = -27$
28. 최고차항의 계수가 $1$인 이차함수 $f(x)$가 모든 실수 $x$에 대하여 $f(x) \gt 0$이다. 상수 $k$에 대하여 함수 $g(x)$를 $$g(x) = \int_{k}^{x}f'(t) \ln f(t) dt$$ 라 하자. 함수 $g(x)$가 $x = a$에서 극대 또는 극소인 모든 $a$를 작은 수부터 크기순으로 나열하면 $a_1$, $a_2$, $a_3$이다. 두 함수 $f(x)$와 $g(x)$가 다음 조건을 만족시킬 때, $f(a_{2})$의 값은? [4점]
(가) 모든 실수 $x$에 대하여 $g(x) \ge 0$이다.
(나) $\displaystyle \int_{a_1}^{a_3}(g(x)+f(x)-f(x)\ln f(x))dx = \frac{3}{2}$
① $\frac{3}{8}$
② $\frac{7}{16}$
③ $\frac{1}{2}$
④ $\frac{9}{16}$
⑤ $\frac{5}{8}$
②
$g(x) = \int_{k}^{x}f'(t) \ln f(t) dt$ $\cdots\cdots$ ㉠
㉠의 양변을 $x$에 대하여 미분하면 $g'(x) = f'(x) \ln f(x)$
$g'(x) = 0$이면 $f'(x) = 0$ 또는 $f(x) = 1$
$f(x)$가 이차함수이므로 일차방정식 $f'(x) = 0$의 실근의 개수는 $1$이고
이차방정식 $f(x) = 1$의 실근의 개수는 최대 $2$이다.
함수 $g(x)$가 $x=a$에서 극대 또는 극소인 모든 $x$의 개수는 $3$이므로 $g'(x) = 0$을 만족시키는 실수 $x$의 개수는 $3$이다. 그러므로 이차방정식 $f(x) = 1$은 서로 다른 두 실근 $\alpha$, $\beta$ ($\alpha \lt \beta$)를 갖는다.
$f(x)-1 = (x-\alpha)(x-\beta)$, $f'(x) = 2x-\alpha-\beta$
방정식 $f'(x) = 0$의 실근은 $x = \frac{\alpha + \beta}{2}$
$\alpha \lt \frac{\alpha + \beta}{2} \lt \beta$에서 $\alpha = a_1$, $\frac{\alpha + \beta}{2} = a_2$, $\beta = a_3$ $\cdots\cdots$ ㉡
즉, $f(x) = (x-a_1)(x-a_3)+1$ $\cdots\cdots$ ㉢
이차함수 $f(x)$의 최고차항의 계수가 양수이므로 $x \to -\infty$일 때 $g'(x) \to -\infty$이고, $x \to \infty$일 때 $g'(x) \to \infty$이다. 즉, 함수 $g(x)$는 $x = a_1$, $x = a_3$에서 극소이고 $x = a_2$에서 극대이다.
㉠의 양변에 $x = k$를 대입하면 $g(k) = 0$이고 조건 (가)에서 함수 $g(x)$의 최솟값은 $0$이므로 함수 $g(x)$는 $x = k$에서 극소이다. 그러므로 $k = a_1$ 또는 $k = a_3$
㉢에서 $f(a_1) = f(a_3) = 1$이므로 $f(k) = 1$
$g(x) = \int_{k}^{x}f'(t)\ln f(t) dt$
$= [\, f(t)\ln f(t)\, ]_{k}^{x}-\int_{k}^{x}(f(t) \times \frac{f'(t)}{f(t)}) dt$
$= f(x) \ln f(x)-f(k) \ln f(k)-f(x)+f(k)$
$= f(x) \ln f(x)-f(x)+1$
조건 (나)에서
$\int_{a_1}^{a_3}(g(x)+f(x)-f(x) \ln f(x))dx = \int_{a_1}^{a_3}1dx = a_{3}-a_1 = \frac{3}{2}$
㉡에서 $a_{1}+a_{3} = 2a_{2}$이므로 $a_{2}-a_1 = \frac{3}{4}$, $a_{2}-a_3 = -\frac{3}{4}$
따라서 $f(a_2) = (a_{2}-a_1)(a_{2}-a_3)+1 = \frac{3}{4} \times (-\frac{3}{4})+1 = \dfrac{7}{16}$
29. 등비수열 $\{ a_n \}$에 대하여 $$\sum_{n=1}^{\infty}(a_{n}+a_{n+1}) = 5, \:\sum_{n=1}^{\infty}\left( |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \right) = 2$$ 일 때, $\displaystyle \sum_{n=1}^{\infty}(100a_{n}-ma_{3n})$의 값이 자연수가 되도록 하는 자연수 $m$의 최댓값을 구하시오. [4점]
$686$
등비수열 $\{ a_n \}$의 첫째항을 $a$, 공비를 $r$이라 하자.
급수 $\displaystyle \sum_{n=1}^{\infty}(a_{n}+a_{n+1})$은 첫째항이 $(a+ar)$, 공비가 $r$인 등비급수이고 그 합이 $5$이므로
$\displaystyle \sum_{n=1}^{\infty}(a_{n}+a_{n+1}) = \frac{a(1+r)}{1-r} = 5$ $\cdots\cdots$ ㉠
㉠에서 $a \gt 0$이다.
(ⅰ) $r = 0$인 경우
$n \ge 2$이면 $a_{n} = 0$이므로
$\displaystyle \sum_{n=1}^{\infty}\left( |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \right) = 0$
(ⅱ) $r \gt 0$인 경우
모든 자연수 $n$에 대하여 $a_{n} = ar^{n-1}$이므로 $a_{n+1}+a_{n+2} \gt 0$이다.
수열 $\{ |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \}$의 항을 첫째항부터
차례로 나열하면 $(a_{2}+a_{3})$, $0$, $-((a_{4}+a_{5}))$, $0$, $\cdots$
$\displaystyle \sum_{n=1}^{\infty}\left( |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \right)$
$= \displaystyle \sum_{n=1}^{\infty}(-1)^{n-1}(a_{2n}+a_{2n+1})$
$= \displaystyle \sum_{n=1}^{\infty}ar(1+r)(-r^{2})^{n-1}$
$= \displaystyle \frac{ar(1+r)}{1+r^2} = 2$ $\cdots\cdots$ ㉡
㉠, ㉡에서 $\frac{2}{5} = \frac{r(1-r)}{1+r^2}$, $7r^{2}-5r+2 = 0$이고 이차방정식 $7r^{2}-5r+2 = 0$의 판별식을 $D$라 하면
$D = (-5)^{2}-4\times 7\times 2$이므로
$r \gt 0$인 실수 $r$는 존재하지 않는다.
(ⅲ) $r \gt 0$인 경우
$-1 \lt r \lt 0$이므로 모든 자연수 $n$에 대하여
$a_{2n}+a_{2n+1} = ar^{2n-1}+ar^{2n} = ar^{2n-1}(1+r) \lt 0$
수열 $\{ |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \}$의 항을 첫째항부터 차례로 나열하면 $-(a_{2}+a_{3})$, $0$, $((a_{4}+a_{5}))$, $0$, $\cdots$
$\displaystyle \sum_{n=1}^{\infty}\left( |\,a_{n+1}+a_{n+2}\,| \times \sin \frac{n\pi}{2} \right)$
$= \displaystyle \sum_{n=1}^{\infty}(-1)^{n}(a_{2n}+a_{2n+1})$
$= \displaystyle -\sum_{n=1}^{\infty}ar(1+r)(-r^{2})^{n-1}$
$= \displaystyle -\frac{ar(1+r)}{1+r^2} = 2$ $\cdots\cdots$ ㉢
㉠, ㉢에서 $-\frac{2}{5} = \frac{r(1-r)}{1+r^2}$, $3r^{2}-5r-2 = 0$
$r = -\frac{1}{3}$ 또는 $r = 2$, $-1 \lt r \lt 0$이므로 $r = -\frac{1}{3}$
(ⅰ), (ⅱ), (ⅲ)에서 $r = -\frac{1}{3}$이고 ㉠에서 $a = 10$
수열 $\{ a_{3n} \}$은 첫째항이 $a_{3} = ar^{2} = \frac{10}{9}$이고 공비가 $r^{3} = -\frac{1}{27}$인 등비수열이므로
$\displaystyle \sum_{n=1}^{\infty}(100a_{n}-ma_{3n})$
$= \displaystyle 100\times \frac{10}{1+\frac{1}{3}}-m\times \frac{\frac{10}{9}}{1+\frac{1}{27}} = 15\times \frac{700-m}{14}$
$14$와 $15$는 서로소이므로 $15\times \frac{700-m}{14}$의 값이 자연수가 되려면 자연수 $k$ ($k \lt 50$)에 대하여 $m = 700-14k$
따라서 자연수 $m$의 최댓값은 $k = 1$일 때 $686$
30. 함수 $f(x) = ax^{3}-2axx^{2}+bx-b-2$가 다음 조건을 만족시키도록 하는 두 정수 $a$ ($a \ne 0$), $b$에 대하여 $h'(-\sqrt{2})$의 최댓값이 $\dfrac{k}{\pi}$일 때, $k^{2}$의 값을 구하시오. [4점]
실수 전체의 집합에서 정의된 함수 $$g(x) = \begin{cases} f(x)+2 & (x \lt 0 \textbf{ 또는 } x \gt 0) \\ -2 \cos \left( \dfrac{\pi}{4}f(x)\right) & (0 \le x \le 2) \end{cases}$$ 는 역함수 $h(x)$를 갖는다.
$8$
함수 $g(x)$는 일대일함수이므로
$|\frac{\pi}{4}(f(2)-f(0))| \le \pi$ 즉, $|f(2)-f(0)| \le 4$
$f(0) = -b-2$, $f(2) = b-2$이므로 $|2b| \le 4$, $-2 \le b \le 2$
$0 \le x_{1} \le 2$, $0 \le x_{2} \le 2$인 $x_1$, $x_2$에 대하여
$f(x_1) = f(x_2)$라 하면 $g(x_1) = g(x_2)$이고
함수 $g(x)$가 역함수를 가지므로 $x_{1} = x_2$
그러므로 함수 $f(x)$는 $0 \le x \le 2$에서 증가하거나 에서 감소한다.
(ⅰ) $b = -1$인 경우
$f(0) = -1$, $f(1) = -a-2$, $f(2) = -3$
$-3 \lt -a-2 \lt -1$인 $a$ ($a \ne 0$)은 존재하지 않는다.
(ⅱ) $b = 0$인 경우
$f(0) = f(2)$, $g(0) = g(2)$이므로 함수 $g(x)$는 일대일함수가 아니다.
(ⅲ) $b = 1$인 경우
$f(0) = -3$, $f(1) = -a-2$, $f(2) = -1$
$-3 \lt -a-2 \lt -1$인 $a$ ($a \ne 0$)은 존재하지 않는다.
(ⅰ), (ⅱ), (ⅲ)에서 $b = -2$ 또는 $b = 2$
$b = -2$이면 $f(0) = 0$, $f(2) = -4$에서 $g(0) = -2$, $g(2) = 2$이므로 함수 $g(x)$는 $0 \le x \le 2$에서 증가한다.
$b = 2$이면 $f(0) = -4$, $f(2) = 0$에서 $g(0) = 2$, $g(2) = -2$이므로 함수 $g(x)$는 $0 \le x \le 2$에서 감소한다.
$h(-\sqrt{2}) = c$라 하면 $g(c) = -\sqrt{2}$이므로 $0 \lt c \lt 2$이다.
$h'(-\sqrt{2}) = \frac{1}{g'(h(-\sqrt{2}))} = \frac{1}{g'(c)}$에서
$b = -2$일 때 $g'(c) \ge 0$이고 $b = 2$일 때 $g'(c) \le 0$이므로
$b = -2$일 때 $h'(-\sqrt{2})$의 값이 최대이다.
$g(0) = -2 \cos (\frac{\pi}{4}f(0)) = -2$, $\displaystyle \lim_{x \to 0-}g(x) = f(0) + 2 = 2$
이고 함수 $g(x)$가 역함수를 가지므로
$x \lt 0$에서 함수 $g(x) = f(x)+2$는 감소한다.
$x \to -\infty$일 때 $f(x) \to \infty$이므로 $a \lt 0$에서 $x \gt 0$일 때 함수 $g(x) = f(x)+2$는 감소한다.
함수 $f(x)$는 $0 \le x \le 2$에서 증가하거나 $0 \le x \le 2$에서 감소하고 $f(0) \gt f(2)$이므로 함수 $f(x)$는 $0 \le x \le 2$에서 감소한다.
즉 함수 $f(x)$는 실수 전체의 집합에서 감소한다.
$b = -2$에서 $f(x) = ax^{3}-2ax^{2}-2x$, $f'(x) = 3ax^{2}-4ax-2$
모든 실수 $x$에 대하여 $f'(x) \le 0$이므로
이차방정식 $3ax^{2}-4ax-2 = 0$의 판별식을 $D$라 하면
$\frac{D}{4} = (-2a)^{2}-3a\times (-2) \le 0$, $2a(2a+3) \le 0$, $-\frac{3}{2} \le a \le 0$
$a$는 음의 정수이므로 $a = -1$
$g(c) = -\sqrt{2}$ ($0 \lt c \lt 2$)이므로 $-2 \cos (\frac{\pi}{4}f(c)) = -\sqrt{2}$
$-4 \lt f(c) \lt 0$이므로 $f(c) = -1$
$-c^{3}+2c^{2}-2c = -1$, $(c-1)(c^{2}-c+1) = 0$, $c = 1$
$\displaystyle h'(-\sqrt{2}) = \frac{1}{g'(1)} = \frac{1}{2 \sin (\frac{\pi}{4}f(1))\times \frac{\pi}{4}f'(1)} = \frac{2\sqrt{2}}{\pi}$
따라서 $k = 2\sqrt{2}$, $k^{2} = 8$
수학 영역(기하)
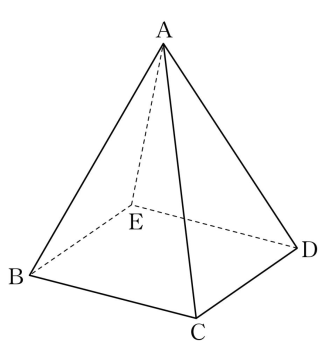
25. 그림과 같이 한 변의 길이가 $2$인 정사각형 $\mathrm{BCDE}$를 밑면으로 하고 $\overline{\mathrm{AB}} = \overline{\mathrm{AC}} = \overline{\mathrm{AD}} = \overline{\mathrm{AE}}$인 사각뿔 $\mathrm{A\text{-}BCDE}$가 있다. 직선 $\mathrm{AC}$와 평면 $\mathrm{BCDE}$가 이루는 각의 크기가 $\dfrac{\pi}{3}$일 때, 삼각형 $\mathrm{ABC}$의 넓이는? [3점]
① $2$
② $\sqrt{5}$
③ $\sqrt{6}$
④ $\sqrt{7}$
⑤ $2\sqrt{2}$
④
점 $\mathrm{A}$에서 평면 $\mathrm{BCDE}$에 내린 수선의 발을 $\mathrm{A}’$이라 하면
$\overline{\mathrm{A’C}} = \frac{1}{2}\times \overline{\mathrm{EC}} = \frac{1}{2}\times 2\sqrt{2} = \sqrt{2}$
직선 $\mathrm{AC}$와 평면 $\mathrm{BCDE}$가 이루는 각의 크기가 $\frac{\pi}{3}$
이므로 $\overline{\mathrm{A’C}} = \overline{\mathrm{AC}}\times \cos \frac{\pi}{3}$, $\overline{\mathrm{AC}} = 2\sqrt{2}$
점 $\mathrm{A}$에서 선분 $\mathrm{BC}$에 내린 수선의 발을 $\mathrm{H}$라 하면 직각삼각형 $\mathrm{AHC}$에서
$\overline{\mathrm{AH}} = \sqrt{\overline{\mathrm{AC}}^{\,2}-\overline{\mathrm{HC}}^{\,2}} = \sqrt{(2\sqrt{2})^{2}-1^{2}} = \sqrt{7}$
따라서 삼각형 $\mathrm{ABC}$의 넓이는 $\frac{1}{2}\times \overline{\mathrm{BC}} \times \overline{\mathrm{AH}} = \sqrt{7}$
26. 좌표공간의 두 점 $\mathrm{A}(a, -5, \,2)$, $\mathrm{B}(2, \,1, \,1)$에 대하여 선분 $\mathrm{AB}$를 $2 : 1$로 내분하는 점을 $\mathrm{P}$, 선분 $\mathrm{AB}$를 $2 : 1$로 외분하는 점을 $\mathrm{Q}$라 하자. 선분 $\mathrm{PQ}$의 중점을 중심으로 하는 구가 $xy$ 평면과 $zx$ 평면에 모두 접할 때, 양수 $a$의 값은? [3점]
① $17$
② $18$
③ $19$
④ $20$
⑤ $21$
①
점 $\mathrm{P}$의 좌표는
$\left( \frac{2\times 2+1\times a}{2+1}, \frac{2\times 1+1\times (-5)}{2+1}, \frac{2\times 1+1\times 2}{2+1} \right)$
즉, $\left( \frac{a+4}{3}, -1, \frac{4}{3} \right)$
점 $\mathrm{Q}$의 좌표는
$\left( \frac{2\times 2-1\times a}{2-1}, \frac{2\times 1-1\times (-5)}{2-1}, \frac{2\times 1-1\times 2}{2-1} \right)$
즉, $\left( 4-a, 7, 0 \right)$
선분 $\mathrm{PQ}$의 중점 $\left( \frac{8-a}{3}, 3, \frac{2}{3} \right)$를 중심으로 하는 구가 $yz$평면과 $zx$평면에 모두 접하므로
$|\frac{8-a}{3}| = 3$ 즉, $\frac{8-a}{3} = 3$ 또는 $\frac{8-a}{3} = -3$
$a = -1$ 또는 $a = 17$에서 $a \gt 0$이므로 $a = 17$
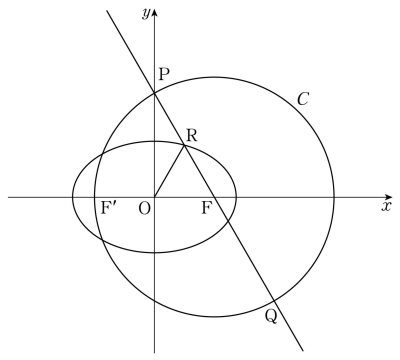
27. 그림과 같이 두 초점이 $\mathrm{F}(c, 0)$, $\mathrm{F'}(-c, 0)$ ($c \gt 0$)이고 장축의 길이가 $12$인 타원이 있다. 점 $\mathrm{F}$를 중심으로 하고 점 $\mathrm{F'}$을 지나는 원을 $C$라 하자. 원 $C$가 $y$축과 만나는 점 중 $y$좌표가 양수인 점을 $\mathrm{P}$라 하고, 원 $C$가 직선 $\mathrm{PF}$와 만나는 점 중 $\mathrm{P}$가 아닌 점을 $\mathrm{Q}$라 하자. 직선 $\mathrm{PQ}$가 타원과 만나는 점 중 제$1$사분면에 있는 점을 $\mathrm{R}$이라 하면 점 $\mathrm{R}$는 선분 $\mathrm{PQ}$를 $1 : 3$으로 내분한다. 선분 $\mathrm{OR}$의 길이는? (단, $\mathrm{O}$는 원점이다.) [3점]
① $8\sqrt{3}-10$
② $7\sqrt{3}-8$
③ $6\sqrt{3}-6$
④ $5\sqrt{3}-4$
⑤ $4\sqrt{3}-2$
③
$y$축이 선분 $\mathrm{FF’}$의 수직이등분선이므로 $\overline{\mathrm{PF’}} = \overline{\mathrm{PF}}$
두 점 $\mathrm{P}$, $\mathrm{F’}$이 원 $C$ 위의 점이므로 $\overline{\mathrm{PF}} = \overline{\mathrm{FF’}} = 2c$
즉, 삼각형 $\mathrm{PF’F}$는 한 변의 길이가 $2c$인 정삼각형이다.
점 $\mathrm{R}$이 선분 $\mathrm{PQ}$를 $1 : 3$으로 내분하고, 점 $\mathrm{F}$가 선분 $\mathrm{PQ}$의 중점이므로 $\overline{\mathrm{FR}} = \frac{1}{2}\times \overline{\mathrm{PF}} = \frac{1}{2}\times 2c = c$
점 $\mathrm{R}$는 정삼각형 $\mathrm{PF’F}$의 변 $\mathrm{PF}$의 중점이므로
삼각형 $\mathrm{FRF’}$은 $\angle \mathrm{FRF’} = \frac{\pi}{2}$인 직각삼각형이다.
$\angle \mathrm{F’FR} = \frac{\pi}{3}$이므로 $\overline{\mathrm{FR}} : \overline{\mathrm{F’R}} = 1 : \sqrt{3}$, $\overline{\mathrm{F’R}} = \sqrt{3}c$
점 $\mathrm{R}$는 타원 위의 점이므로 $\overline{\mathrm{F’R}} + \overline{\mathrm{FR}} = 12$
$\sqrt{3}c+c = 12$, $c = 6\sqrt{3}-6$
$\angle \mathrm{OFR} = \frac{\pi}{3}$, $\overline{\mathrm{FR}} = \overline{\mathrm{FO}} = c$이므로
삼각형 $\mathrm{ROF}$는 한 변의 길이가 $c$인 정삼각형이다.
따라서 $\overline{\mathrm{OR}} = c = 6\sqrt{3}-6$
28. 좌표공간에 서로 평행한 두 평면 $\alpha$, $\beta$와 중심이 $\mathrm{O}$이고 반지름의 길이가 $\sqrt{13}$인 구 $S$가 있다. 점 $\mathrm{O}$에서 두 평면 $\alpha$, $\beta$에 내린 수선의 발을 각각 $\mathrm{H}_1$, $\mathrm{H}_2$라 하면 $\overline{\mathrm{OH_1}} = \overline{\mathrm{OH_2}} = 2$이다. 구 $S$가 평면 $\alpha$와 만나서 생기는 원 위를 움직이는 점을 $\mathrm{P}$, 구 $S$가 평면 $\beta$와 만나서 생기는 원 위를 움직이는 점 $\mathrm{Q}$을 라 하자.
삼각형 $\mathrm{POQ}$의 평면 $\beta$ 위로의 정사영의 넓이가 최대일 때, 평면 $\mathrm{POQ}$와 평면 $\beta$가 이루는 각의 크기를 $\theta$라 하자. $\cos \theta$의 값은? (단, 세 점 $\mathrm{O}$, $\mathrm{P}$, $\mathrm{Q}$는 한 직선 위에 있지 않고, 직선 $\mathrm{PQ}$와 직선 $\mathrm{H_{1}H_2}$는 서로 평행하지 않다.) [4점]
① $\frac{2\sqrt{17}}{17}$
② $\frac{5\sqrt{17}}{34}$
③ $\frac{3\sqrt{17}}{17}$
④ $\frac{7\sqrt{17}}{34}$
⑤ $\frac{4\sqrt{17}}{17}$
③
구 $S$의 반지름의 길이가 $\sqrt{13}$이므로
$\overline{\mathrm{PH_1}} = \sqrt{(\sqrt{13})^{2}-2^{2}} = 3$, $\overline{\mathrm{QH_2}} = \sqrt{(\sqrt{13})^{2}-2^{2}} = 3$
점 $\mathrm{P}$의 평면 $\beta$ 위로의 정사영을 $\mathrm{P’}$이라 하자.
삼각형 $\mathrm{POQ}$의 평면 $\beta$ 위로의 정사영은 삼각형 $\mathrm{P’H_{2}Q}$이다.
삼각형 $\mathrm{P’H_{2}Q}$의 넓이는 $\frac{1}{2}\times \overline{\mathrm{P’H_{2}}}\times \overline{\mathrm{QH_{2}}}\times \sin (\angle \mathrm{P’H_{2}Q})$이므로 $\angle \mathrm{P’H_{2}Q} = \frac{\pi}{2}$일 때 최대이다.
직선 $\mathrm{PO}$가 평면 $\beta$와 만나는 점을 $\mathrm{R}$이라 하자.
선분 $\mathrm{P’R}$는 구 $S$가 평면 $\beta$와 만나서 생기는 원의 지름이므로 $\overline{\mathrm{P’Q}} \perp \overline{\mathrm{QR}}$이다.
$\overline{\mathrm{PP’}} \perp \beta$, $\overline{\mathrm{P’Q}} \perp \overline{\mathrm{QR}}$이므로 삼수선의 정리에 의하여 $\overline{\mathrm{PQ}} \perp \overline{\mathrm{QR}}$이고 직선 $\mathrm{QR}$이 평면 $\mathrm{Pㅃㄲ}$와 평면 $\beta$의 교선이므로 $\theta = \angle \mathrm{PQP’}$
직각삼각형 $\mathrm{P’H_{2}Q}$에서 $\overline{\mathrm{P’Q}} = \sqrt{3^{2}+3^{2}} = 3\sqrt{2}$
직각삼각형 $\mathrm{PP’Q}$에서 $\overline{\mathrm{PQ}} = \sqrt{(3\sqrt{2})^{2}+4^{2}} = \sqrt{34}$
$\cos \theta = \dfrac{\overline{\mathrm{P’Q}}}{\overline{\mathrm{PQ}}} = \dfrac{3\sqrt{2}}{\sqrt{34}} = \dfrac{3\sqrt{17}}{17}$
29. 두 초점이 $\mathrm{F}(c, 0)$, $\mathrm{F'}(-c, 0)$ ($c \gt 0$)인 쌍곡선 $C$가 있다. 이 쌍곡선 위에 있는 제$1$사분면 위의 점 $\mathrm{P}$에 대하여 직선 $\mathrm{PF}$는 쌍곡선 $C$의 한 점근선과 평행하다. 직선 $\mathrm{PF}$가 $y$축과 만나는 점을 $\mathrm{Q}$라 할 때, $$\angle \mathrm{QPF'} = \frac{\pi}{2}, \:\overline{\mathrm{QF}} = 20$$ 이다. 삼각형 $\mathrm{OPQ}$의 넓이를 구하시오. (단, $\mathrm{O}$는 원점이다.) [4점]
$48$
쌍곡선 $C$의 방정식을 $\frac{x^2}{a^2}-\frac{y^2}{b^2} = 1$ ($a \gt 0$, $b \gt 0$)이라 하면 쌍곡선 $C$의 점근선의 방정식은 $y = \pm \frac{b}{a}x$
점 $\mathrm{P}$가 제$1$사분면 위에 있으므로 직선 $\mathrm{PF}$와 직선 $y = \frac{b}{a}x$는 서로 평행하지 않다.
그러므로 직선 $\mathrm{PF}$의 기울기는 $-\frac{b}{a}$
$\angle \mathrm{QPF’} = \frac{\pi}{2}$이므로 직선 $\mathrm{PF’}$의 기울기는 $\frac{a}{b}$
$\overline{\mathrm{PF’}} : \overline{\mathrm{PF}} = b : a$에서 $\overline{\mathrm{PF’}} = bt$, $\overline{\mathrm{PF}} = at$ ($t \gt 0$)이라 하자.
$\overline{\mathrm{FF’}} = 2c$이므로 직각삼각형 $\mathrm{FPF’}$에서
$\overline{\mathrm{PF}}^{2}+\overline{\mathrm{PF’}}^{2} = \overline{\mathrm{F’F}}^{2}$, $(at)^{2}+(bt)^{2} = (2c)^{2}$
$t^{2}(a^{2}+b^2) = 4c^2$ $\cdots\cdots$ ㉠
쌍곡선 $C$의 초점 $\mathrm{F}$의 $x$좌표가 $c$이므로
$a^{2}+b^{2} = c^2$ $\cdots\cdots$ ㉡
㉠에 ㉡을 대입하면 $t^{2}c^{2} = 4c^2$, $t^{2} = 4$
$t \gt 0$이므로 $t = 2$, 즉, $\overline{\mathrm{PF’}} = 2b$, $\overline{\mathrm{PF}} = 2a$
점 $\mathrm{P}$가 쌍곡선 $C$ 위의 점이므로 $\overline{\mathrm{PF’}}-\overline{\mathrm{PF}} = 2a$
$2b-2a = 2a$, $b = 2a$
㉡에 를 $b = 2a$대입하면 $a^{2}+(2a)^{2} = c^2$, $c = \sqrt{5}a$
직선 $\mathrm{PF}$의 기울기가 $-\frac{b}{a} = -2$이므로 $\overline{\mathrm{OF}} : \overline{\mathrm{OQ}} = 1 : 2$
$\overline{\mathrm{OF}} = c = \sqrt{5}a$에서 $\overline{\mathrm{OQ}} = 2\sqrt{5}a$
직각삼각형 $\mathrm{QOF}$에서
$\overline{\mathrm{PF}}^{2}+\overline{\mathrm{OQ}}^{2} = \overline{\mathrm{QF}}^{2}$, $(\sqrt{5}a)^{2}+(2\sqrt{5}a)^{2} = 20^{2}$, $a = 4$
$\overline{\mathrm{PF}} = 2a = 8$, $\overline{\mathrm{QP}} = \overline{\mathrm{QF}}-\overline{\mathrm{PF}} = 20-8 = 12$이므로
점 $\mathrm{P}$는 선분 $\mathrm{QF}$를 $3 : 2$로 내분하는 점이다.
따라서 삼각형 $\mathrm{OPQ}$의 넓이는
$\frac{3}{5}\times \frac{1}{2} \times \overline{\mathrm{OF}} \times \overline{\mathrm{OQ}} = \frac{3}{5}\times \frac{1}{2} \times 4\sqrt{5} \times 8\sqrt{5}$ $= 48$
30. 좌표평면에 한 변의 길이가 $8$인 정사각형 $\mathrm{ABCD}$와 $$\overrightarrow{\mathrm{AE}} = \overrightarrow{\mathrm{AD}}-\frac{1}{2}\overrightarrow{\mathrm{AB}}$$ 를 만족시키는 점 $\mathrm{E}$가 있다. 선분 $\mathrm{BC}$를 지름으로 하는 원 위를 움직이는 점 $\mathrm{P}$에 대하여 점 $\mathrm{Q}$가 다음 조건을 만족시킨다.
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} \ge 0$이면 $\overrightarrow{\mathrm{BQ}}+\overrightarrow{\mathrm{CQ}} = 4\overrightarrow{\mathrm{PQ}}$이고,
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} \lt 0$이면 $\overrightarrow{\mathrm{BQ}}+\overrightarrow{\mathrm{CQ}} = 6\overrightarrow{\mathrm{PQ}}$이다.
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 최댓값과 최솟값을 각각 $M$, $m$이라 할 때, $(M+m)^2$의 값을 구하시오. [4점]
$320$
$\overrightarrow{\mathrm{AE}} = \overrightarrow{\mathrm{AD}}+\frac{1}{2}\overrightarrow{\mathrm{BA}}$에서 점 $\mathrm{E}$는 $\overline{\mathrm{DE}} = 4$, $\angle \mathrm{ADE} = \frac{\pi}{2}$인 직각삼각형 $\mathrm{ADE}$의 한 꼭짓점이다.
선분 $\mathrm{BC}$를 지름으로 하는 원을 $C$, 점 $\mathrm{A}$를 지나면서 직선 $\mathrm{AE}$에 수직인 직선을 $l$이라 하자.
직선 $l$이 선분 $\mathrm{BC}$와 만나는 점을 $\mathrm{O}$라 하면 $\overline{\mathrm{AB}} : \overline{\mathrm{BO}} = \overline{\mathrm{AD}} : \overline{\mathrm{DE}} = 2 : 1$이므로 점 $\mathrm{O}$는 선분 $\mathrm{BC}$의 중점이다. 즉, 점 $\mathrm{O}$는 원 $C$의 중심이다.
직선 $l$이 원 $C$와 만나는 두 점 중 점 $\mathrm{A}$와 가까운 점을 $\mathrm{A_1}$,
다른 한 점을 $\mathrm{A_2}$라 하자.
두 벡터 $\overrightarrow{\mathrm{AE}}$, $\overrightarrow{\mathrm{AP}}$가 이루는 각의 크기를 $\theta$ ($0 \le \theta \le \pi$)라 하자.
(ⅰ) $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} \ge 0$인 경우
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} = |\overrightarrow{\mathrm{AE}}||\overrightarrow{\mathrm{AP}}| \cos \theta \ge 0$을 만족시키는 $\theta$의 값의 범위는 $0 \le \theta \le \frac{\pi}{2}$
점 $\mathrm{P}$는 점 $\mathrm{C}$를 포함하는 호 $\mathrm{A_{1}A_2}$ 위의 점이다.
$\overrightarrow{\mathrm{BQ}}+\overrightarrow{\mathrm{CQ}} = 4\overrightarrow{\mathrm{PQ}}$에서
$(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OB}})+(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OC}}) = 4(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}})$, $\overrightarrow{\mathrm{OQ}} = 2\overrightarrow{\mathrm{OP}}$
두 벡터 $\overrightarrow{\mathrm{AE}}$, $\overrightarrow{\mathrm{AQ}}$가 이루는 각의 크기를 $\theta_1$이라 하자. 점 $\mathrm{P}$는 중심이 $\mathrm{O}$이고 반지름의 길이가 $4$인 원 위의 점이므로 점 $\mathrm{Q}$는 중심이 $\mathrm{O}$이고 반지름의 길이가 $8$인 원 위의 점 중 $0 \le \theta_{1} \le \frac{\pi}{2}$를 만족시키는 점이다.
(ⅱ) $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} \lt 0$인 경우
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AP}} = |\overrightarrow{\mathrm{AE}}||\overrightarrow{\mathrm{AP}}| \cos \theta \lt 0$을 만족시키는 $\theta$의 값의 범위는 $\frac{\pi}{2} \lt \theta \lt \pi$
점 $\mathrm{P}$는 점 $\mathrm{B}$를 포함하는 호 $\mathrm{A_{1}A_2}$ 위의 점이다.
$\overrightarrow{\mathrm{BQ}}+\overrightarrow{\mathrm{CQ}} = 6\overrightarrow{\mathrm{PQ}}$에서
$(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OB}})+(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OC}}) = 6(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}})$, $\overrightarrow{\mathrm{OQ}} = \frac{3}{2}\overrightarrow{\mathrm{OP}}$
두 벡터 $\overrightarrow{\mathrm{AE}}$, $\overrightarrow{\mathrm{AQ}}$가 이루는 각의 크기를 $\theta_2$라 하자. 점 $\mathrm{P}$는 중심이 $\mathrm{O}$이고 반지름의 길이가 $4$인 원 위의 점이므로 점 $\mathrm{Q}$는 중심이 $\mathrm{O}$이고 반지름의 길이가 $6$인 원 위의 점 중 $\frac{\pi}{2} \lt \theta_{2} \le \pi$를 만족시키는 점이다.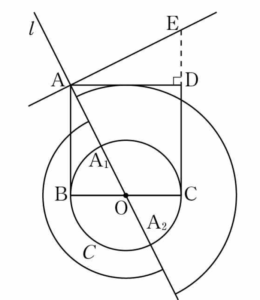
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}} = \overrightarrow{\mathrm{AE}}\cdot(\overrightarrow{\mathrm{AO}}+\overrightarrow{\mathrm{OQ}})$
$= \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AO}}+\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{OQ}}$
$= \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{OQ}}$
$|\overrightarrow{\mathrm{AE}}| = \sqrt{8^{2}+4^2} = 4\sqrt{5}$
두 벡터 $\overrightarrow{\mathrm{OQ}}$, $\overrightarrow{\mathrm{AE}}$가 서로 평행하고 방향이 같을 때 $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 값이 최대이고,
두 벡터 $\overrightarrow{\mathrm{OQ}}$, $\overrightarrow{\mathrm{AE}}$가 서로 평행하고 방향이 반대일 때 $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 값이 최소이므로
(ⅰ)에서 $M = |\overrightarrow{\mathrm{AE}}| \times |\overrightarrow{\mathrm{AQ}}|$ $= 4\sqrt{5} \times 8 = 32\sqrt{5}$
(ⅱ)에서 $m = -|\overrightarrow{\mathrm{AE}}| \times |\overrightarrow{\mathrm{AQ}}|$ $= -4\sqrt{5} \times 6 = -24\sqrt{5}$
따라서 $(M+m)^{2} = (8\sqrt{5})^{2} = 320$