25년 10월 고1 교육청
3. 두 행렬 $A = \begin{pmatrix} 2 & 0 \\ 3 & -1 \end{pmatrix}$, $B = \begin{pmatrix} 1 & 2 \\ 0 & 2 \end{pmatrix}$에 대하여 행렬 $A+2B$의 모든 성분의 합은? [2점]
① $10$
② $12$
③ $14$
④ $16$
⑤ $18$
③
$A+2B = \begin{pmatrix} 2 & 0 \\ 3 & -1 \end{pmatrix} +2\begin{pmatrix} 1 & 2 \\ 0 & 2 \end{pmatrix}$
$= \begin{pmatrix} 2 & 0 \\ 3 & -1 \end{pmatrix} +\begin{pmatrix} 2 & 4 \\ 0 & 4 \end{pmatrix}$
$= \begin{pmatrix} 2+2 & 0+4 \\ 3+0 & -1+4 \end{pmatrix}$
$= \begin{pmatrix} 4 & 4 \\ 3 & 3 \end{pmatrix}$
이므로 구하는 모든 성분의 합은
$4+4+3+3 = 14$
5. 좌표평면 위의 점 $(3, a)$를 점 $(8, 8)$로 옮기는 평행이동에 의하여 점 $(5, 5)$가 점 $(b, 2)$로 옮겨질 때, $a+b$의 값은? [3점]
① $21$
② $23$
③ $25$
④ $27$
⑤ $29$
7. 두 이차정사각행렬 $A$, $B$의 $(i, j)$ 성분을 각각 $a_{ij}$, $b_{ij}$라 할 때, $$a_{ij} = i+2j \:\:(i = 1, 2, \,j = 1, 2),$$ $$b_{ij} = i\times j \:\:(i = 1, 2, \,j = 1, 2)$$ 이다. 행렬 $AB$의 $()$2, 1성분은? [3점]
① $4$
② $7$
③ $10$
④ $13$
⑤ $16$
8. 연립방정식 $$\begin{cases} x-y = -3 \\ \\ x^{2}-6x+4y = 11 \end{cases}$$ 의 해를 $x = \alpha$, $y = \beta$라 할 때, $\alpha+\beta$의 값은? [3점]
① $3$
② $4$
③ $5$
④ $6$
⑤ $7$
10. 한 개의 주사위를 두 번 던져서 나오는 눈의 수를 차례로 $a$, $b$라 하자. $a\times b$가 $4$의 약수 또는 $12$의 배수가 되는 모든 순서쌍 $(a, b)$의 개수는? [3점]
① $7$
② $9$
③ $11$
④ $13$
⑤ $15$
④
(ⅰ) $a\times b$가 $4$의 약수인 경우
$a\times b = 1$이 되는 순서쌍 $(a, b)$는 $(1, 1)$의 $1$가지
$a\times b = 2$가 되는 순서쌍 $(a, b)$는 $(1, 2)$, $(2, 1)$의 $2$가지
$a\times b = 4$가 되는 순서쌍 $(a, b)$는 $(1, 4)$, $(2, 2)$, $(4, 1)$의 $3$가지
그러므로 구하는 모든 순서쌍 $(a, b)$의 개수는
$1+2+3 = 6$
(ⅱ) $a\times b$가 $12$의 배수인 경우
$a\times b = 12$가 되는 순서쌍 $(a, b)$는 $(2, 6)$, $(3, 4)$, $(4, 3)$, $(6, 2)$의 $4$가지
$a\times b = 24$가 되는 순서쌍 $(a, b)$는 $(4, 6)$, $(6, 4)$의 $2$가지
$a\times b = 36$이 되는 순서쌍 $(a, b)$는 $(6, 6)$의 $1$가지
그러므로 구하는 모든 순서쌍 $(a, b)$의 개수는
$4+2+1 = 7$
(ⅰ), (ⅱ)에 의하여 구하는 모든 순서쌍 $(a, b)$의 개수는 $6+7 = 13$
11. 점 $(m, -m)$과 직선 $3x+y+3 = 0$ 사이의 거리를 $d_1$, 점 $(0, 5)$와 직선 $3x+y+3 = 0$ 사이의 거리를 $d_1$라 하자. $d_{1} \lt d_2$가 되도록 하는 정수 $m$의 개수는? [3점]
① $8$
② $10$
③ $12$
④ $14$
⑤ $16$
①
점 $(m, -m)$과 직선 $3x+y+3 = 0$ 사이의 거리 $d_1$은
$d_{1} = \frac{|\,3\times m + 1 \times (-m) + 3 \,|}{\sqrt{3^{2}+1^{2}}}$ $ = \frac{|\,2m + 3 \,|}{\sqrt{10}}$
점 $(0, 5)$와 직선 $3x+y+3 = 0$ 사이의 거리 $d_2$는
$d_{2} = \frac{|\,3\times 0 + 1 \times 5 + 3 \,|}{\sqrt{3^{2}+1^{2}}}$ $ = \frac{8}{\sqrt{10}}$
$d_{1} \lt d_2$이므로 $\frac{|\,2m + 3 \,|}{\sqrt{10}} \lt \frac{8}{\sqrt{10}}$에서
$|\,2m + 3 \,| \lt 8$, $-8 \lt 2m+3 \lt 8$
그러므로 $-\frac{11}{2} \lt m \lt \frac{5}{2}$를 만족시키는 정수 $m$은
$-5$, $-4$, $-3$, $-2$, $-1$, $0$, $1$, $2$
따라서 구하는 정수 $m$의 개수는 $8$
곡선 $y=f(x)$ 와 직선 $y=\sin \left( \frac{k}{6}\pi \right)$ 의 교점의 개수는
방정식 $f(x)=\sin \left( \frac{k}{6}\pi \right)$ 의 서로 다른 실근의 개수와 같다. 즉,
(ⅰ) $0 \leq x \leq \frac{k}{6} \pi$ 일 때,
$\sin x = \sin \left( \frac{k}{6}\pi \right)$
(ⅱ) $\frac{k}{6} \pi < x \leq 2 \pi$ 일 때,
$2 \sin \left( \frac{k}{6}\pi \right) – \sin x = \sin \left( \frac{k}{6}\pi \right)$ 에서 $\sin x = \sin \left( \frac{k}{6}\pi \right)$
그러므로 교점의 개수는 구간 $[0,\, 2 \pi]$ 에서 방정식
$\sin x = \sin \left( \frac{k}{6}\pi \right)$의 서로 다른 실근의 개수와 같다.
$k=1$, $k=5$ 일 때, $\sin \left( \frac{k}{6}\pi \right) = \frac{1}{2}$ 이므로
$\sin x = \frac{1}{2}$ 의 서로 다른 실근의 개수는 각각 $2$ 이다.
$k=2$, $k=4$ 일 때, $\sin \left( \frac{k}{6}\pi \right) = \frac{\sqrt{3}}{2}$ 이므로
$\sin x = \frac{\sqrt{3}}{2}$ 의 서로 다른 실근의 개수는 각각 $2$ 이다.
$k=3$ 일 때, $\sin \left( \frac{k}{6}\pi \right) = 1$ 이므로
$\sin x = 1$ 의 서로 다른 실근의 개수는 각각 $1$ 이다.
따라서 $a_{1}+a_{2}+a_{3}+a_{4}+a_{5}$ $=2+2+1+2+2=9$
12. 실수 $a$에 대하여 복소수 $z$를 라 $z = a^{2}+(1+i)a-6(2+i)$하자. $z^{2}$이 실수가 되도록 하는 모든 $a$의 값의 합은? (단, $i = \sqrt{-1}$) [3점]
① $-4$
② $-1$
③ $2$
④ $5$
⑤ $8$
13. $x$에 대한 연립부등식 $$\begin{cases} x^{2} \ge 4n^{2} \\ \\ x^{2}-nx-6n^{2} \le 0 \end{cases}$$ 을 만족시키는 정수 $x$의 개수가 $10$이 되도록 하는 자연수 $n$의 값은? [3점]
① $4$
② $6$
③ $8$
④ $10$
⑤ $12$
③
$\begin{cases} x^{2} \ge 4n^{2} & \cdots \text{㉠} \\ x^{2}-nx-6n^{2} \le 0 & \cdots \text{㉡} \end{cases}$
㉠에서 $x^{2}-4n^{2} \ge 0$, $(x+2n)(x-2n) \ge 0$
㉡에서 $(x+2n)(x-3n) \le 0$
$n$이 자연수이므로
$x \le -2n$ 또는 $x \ge 2n$, $-2n \le n \le 3n$
그러므로 $x = -2n$ 또는 $2n \le x \le 3n$
연립부등식을 만족시키는 정수 $x$의 개수는
$1 + (3n-2n+1) = n+2$
따라서 연립부등식을 만족시키는 정수 $x$의 개수가 $10$이 되도록 하는 자연수 $n$의 값은 $8$
14. 좌표평면 위에 두 점 $\mathrm{A}(-3, 2)$, $\mathrm{B}(2, 6)$이 있다. $\overline{\mathrm{PQ}} = 1$인 $x$축 위의 두 점 $\mathrm{P}$, $\mathrm{Q}$에 대하여 $\overline{\mathrm{AP}} + \overline{\mathrm{QB}}$의 최솟값은? (단, 점 $\mathrm{P}$의 $x$좌표는 점 $\mathrm{Q}$의 $x$좌표보다 작다.) [4점]
① $2\sqrt{17}$
② $6\sqrt{2}$
③ $2\sqrt{19}$
④ $4\sqrt{5}$
⑤ $2\sqrt{21}$
④
점 $\mathrm{A}$를 $x$축에 대하여 대칭이동한 점을 $\mathrm{A}’$이라 하면 점 $\mathrm{A}’$의 좌표는 $(-3, -2)$이다.
점 $\mathrm{B}$를 $x$축의 방향으로 $-1$만큼 평행이동한 점을 $\mathrm{B}’$이라 하면 점 $\mathrm{B}’$의 좌표는 $(1, 6)$이다.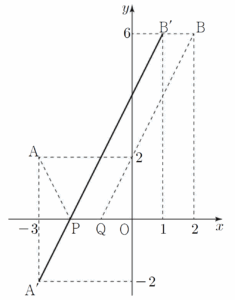
$\overline{\mathrm{AP}} = \overline{\mathrm{A’P}}$, $\overline{\mathrm{QB}} = \overline{\mathrm{PB’}}$이므로
$\overline{\mathrm{AP}} + \overline{\mathrm{QB}} = \overline{\mathrm{A’P}} + \overline{\mathrm{PB’}} \ge \overline{\mathrm{A’B’}}$
점 $\mathrm{P}$가 선분 $\mathrm{A’B’}$ 위에 있을 때 $\overline{\mathrm{AP}} + \overline{\mathrm{QB}}$는 최소이고, 그 값은
$\overline{\mathrm{A’B’}} = \sqrt{\{ 1-(-3) \}^{2}+\{ 6-(-2) \}^{2} } = 4\sqrt{5}$
따라서 $\overline{\mathrm{AP}} + \overline{\mathrm{QB}}$의 최솟값은 $4\sqrt{5}$
15. 세 이차정사각행렬 $A = \begin{pmatrix} 0 & 0 \\ 6 & 0 \end{pmatrix}$, $B$, $C$가 다음 조건을 만족시킨다.
(가) $AB = CA = O$
(나) 행렬 $B$의 모든 성분의 합이 $3$이고,
행렬 $C$의 $(1, 1)$성분과 $(2, 1)$성분이 같다.
$BC = A$일 때, 행렬 $C$의 모든 성분의 합은? (단, $O$는 영행렬이다.) [4점]
① $3$
② $4$
③ $5$
④ $6$
⑤ $7$
②
$B = \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}$, $C = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{pmatrix}$라 하자.
조건 (가)에서
$AB = \begin{pmatrix} 0 & 0 \\ 6 & 0 \end{pmatrix} \begin{pmatrix} b_{11} & b_{12} \\ b_{21} & b_{22} \end{pmatrix}$
$= \begin{pmatrix} 0 & 0 \\ 6b_{11} & 6b_{12} \end{pmatrix} = O$
이므로 $b_{11} = b_{12} = 0$이고,
$CA = \begin{pmatrix} c_{11} & c_{12} \\ c_{21} & c_{22} \end{pmatrix} \begin{pmatrix} 0 & 0 \\ 6 & 0 \end{pmatrix}$
$= \begin{pmatrix} 6c_{12} & 0 \\ 6c_{22} & 0 \end{pmatrix} = O$
이므로 $c_{12} = c_{22} = 0$이다.
조건 (나)에서 $b_{21} + b_{22} = 3$, $c_{11} = c_{21}$
$BC = A$이므로
$\begin{pmatrix} 0 & 0 \\ b_{21} & 3-b_{21} \end{pmatrix} \begin{pmatrix} c_{11} & 0 \\ c_{11} & 0 \end{pmatrix}$
$= \begin{pmatrix} 0 & 0 \\ 3c_{11} & 0 \end{pmatrix} = \begin{pmatrix} 0 & 0 \\ 6 & 0 \end{pmatrix}$
에서 $c_{11} = 2$
그러므로 $C = \begin{pmatrix} 2 & 0 \\ 2 & 0 \end{pmatrix}$
따라서 행렬 $C$의 모든 성분의 합은 $4$
16. $1$학년 학생 $3$명, $2$학년 학생 $2$명, $3$학년 학생 $1$명이 있다. 이 $6$명의 학생 중에서 $5$명의 학생을 선택하고 이 $5$명의 학생이 모두 한 번씩 발표하도록 순서를 정하려고 할 때, $1$학년 학생끼리는 연속해서 발표하지 않도록 순서를 정하는 경우의 수는? (단, 발표는 한 명씩 한다.) [4점]
① $228$
② $234$
③ $240$
④ $246$
⑤ $252$
⑤
(ⅰ) 발표하는 $5$명의 학생 중 $1$학년 학생이 $3$명인 경우
$1$학년 학생 $3$명의 발표 순서를 정하는 경우의 수는 $3! = 6$
$1$학년 학생의 발표 순서를 ㉠, ㉡, ㉢이라 하고 발표 순서를 그림으로 나타내면 학년 학생끼리는 연속해서 발표하지 않아야 하므로 $\vee$로 표시된 두 곳에서 $2$학년 또는 $3$학년 학생이 발표해야 한다.
$\text{㉠}\vee\text{㉡}\vee\text{㉢}$
$2$학년 학생 $2$명과 $3$학년 학생 $1$명 중에서 $2$명을 선택하여 발표 순서를 정하는 경우의 수는 ${}_{3}\mathrm{P}_{2} = 6$
그러므로 구하는 경우의 수는 $6 \times 6 = 36$
(ⅱ) 발표하는 $5$명의 학생 중 $1$학년 학생이 $2$명인 경우
$1$학년 학생 $3$명 중에서 $2$명의 학생을 선택하는 경우의 수는 ${}_{3}\mathrm{C}_{2} = 3$
$2$학년 학생 $2$명과 $3$학년 학생 $1$명 모두 발표해야 하므로 이 $3$명의 발표 순서를 정하는 경우의 수는 $3! = 6$
$2$학년 학생과 $3$학년 학생의 발표 순서를 ⓐ, ⓑ, ⓒ라 하고 발표 순서를 그림으로 나타내면 $1$학년 학생끼리는 연속해서 발표하지 않아야 하므로 $\vee$로 표시된 네 곳 중 두 곳에서 $1$학년 학생이 발표해야 한다.
$\vee\text{ⓐ}\vee\text{ⓑ}\vee\text{ⓒ}\vee$
$1$학년 학생 $2$명의 발표 순서를 정하는 경우의 수는 ${}_{4}\mathrm{P}_{2} = 12$
그러므로 구하는 경우의 수는 $3 \times 6 \times 12 = 216$
(ⅰ), (ⅱ)에 의하여 구하는 경우의 수는
$36+216 = 252$
17. 양수 $a$에 대하여 $0 \le x \le a$에서 이차함수 $f(x) = -2x^{2}+16x-7$의 최댓값과 최솟값의 합이 $0$이 되도록 하는 모든 $a$의 값의 합은? [4점]
① $\frac{17}{2}$
② $9$
③ $\frac{19}{2}$
④ $10$
⑤ $\frac{21}{2}$
④
$f(x) = -2x^{2}+16x-7 = -2(x-4)^{2}+25$
함수 $Y = f(x)$의 그래프는 그림과 같다.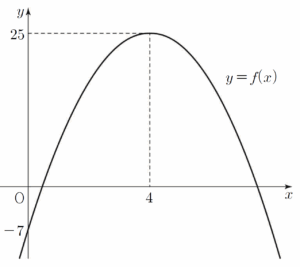
(ⅰ) $0 \lt a \le 4$일 때
$0 \le x \le a$에서 함수 $f(x)$의 최솟값은 $f(0) = -7$이므로
함수 $f(x)$의 최댓값과 최솟값의 합이 $0$이려면 $f(a) = 7$이어야 한다.
$f(a) = -2a^{2}+16a-7 = 7$에서
$2(a-1)(a-7) = 0$, $a = 1$
(ⅱ) $a \gt 4$일 때
$0 \le x \le a$에서 함수 $f(x)$의 최댓값은 $f(4) = 25$이므로
함수 $f(x)$의 최댓값과 최솟값의 합이 $0$이려면 $f(a) = -25$이어야 한다.
$f(a) = -2a^{2}+16a-7 = -25$에서
$2(a+1)(a-9) = 0$, $a = 9$
(ⅰ), (ⅱ)에 의하여 구하는 모든 양수 $a$의 값의 합은
$1+9 = 10$
18. $x$에 대한 다항식 $x^{3}+(2a+3)x^{2}+(3a+5)x+a+3$이 $(x+b)(x+c)^2$으로 인수분해되도록 하는 세 실수 $a$, $b$, $c$에 대하여 $a+b+c$의 최댓값을 $M$, 최솟값을 $m$이라 할 때, $M+m$의 값은? [4점]
① $5$
② $6$
③ $7$
④ $8$
⑤ $9$
②
다항식 $x^{3}+(2a+3)x^{2}+(3a+5)x+a+3$을 조립제법을 이용하여 인수분해하면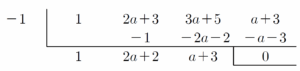
$x^{3}+(2a+3)x^{2}+(3a+5)x+a+3 = (x+1)\{ x^{2}+(2a+2)x+a+3\}$
(ⅰ) 다항식 $x^{2}+(2a+2)x+a+3$이 $x+1$을 인수로 가질 때
인수정리에 의하여
$(-1)^{2}+(2a+2)\times (-1)+a+3 = 0$에서 $a=2$
$(x+1)\{ x^{2}+(2a+2)x+a+3\} = (x+1)(x^{2}+6x+5) = (x+5)(x+1)^2$
에서 $b=5$, $c=1$
그러므로 $a+b+c = 2+5+1 = 8$
(ⅱ) 다항식 $x^{2}+(2a+2)x+a+3$이 $x+1$을 인수로 갖지 않을 때
다항식 $x^{2}+(2a+2)x+a+3$이 완전제곱식이어야 하므로 $(a+1)^{2} = a+3$,
$(a+2)(a-1) = 0$에서 $a = -2$ 또는 $a=1$
(a) $a = -2$일 때
$(x+1)\{ x^{2}+(2a+2)x+a+3\} = (x+1)(x^{2}-2x+1) = (x+1)(x-1)^2$
에서 $b=1$, $c=-1$
그러므로 $a+b+c = -2+1+(-1) = -2$
(b) $a=1$일 때
$(x+1)\{ x^{2}+(2a+2)x+a+3\} = (x+1)(x^{2}+4x+4) = (x+1)(x+2)^2$
에서 $b=1$, $c=2$
그러므로 $a+b+c = 1+1+2 = 4$
(ⅰ), (ⅱ)에 의하여 $M = 8$, $m = -2$이므로
$M+m = 6$
19. 최고차항의 계수가 $1$인 삼차다항식 $f(x)$와 모든 항의 계수가 실수인 두 다항식 $P(x)$, $Q(x)$가 다음 조건을 만족시킨다.
(가) $f(x)$를 $P(x)$로 나누었을 때의 몫은 $Q(x)$이고 나머지는 $P(x)+\{ Q(x)\}^{2}$이다.
(나) $f(x)$를 $Q(x)$로 나누었을 때의 몫은 $P(x)$이고 나머지는 $P(x)+\{ Q(x)\}^{2}$이다.
$P(0) = -2$, $Q(0) = 1$일 때, $f(2)$의 값은? [4점]
① $-3$
② $-2$
③ $-1$
④ $0$
⑤ $1$
⑤
조건 (가), (나)에 의하여 $f(x)$를 $P(x)$로 나누었을 때와 $f(x)$를 $Q(x)$로 나누었을 때의 나머지가 모두 $P(x)+\{ Q(x)\}^{2}$이므로 다항식 $P(x)+\{ Q(x)\}^{2}$의 차수는 두 다항식 $P(x)$, $Q(x)$의 차수보다 작다. $\cdots\cdots$ ㉠
(ⅰ) $Q(x)$의 차수가 $2$ 이상일 때
$P(x)$의 차수는 $1$ 이하이므로 $P(x)+\{ Q(x)\}^{2}$의 차수가 $4$ 이상이 되어 ㉠을 만족시키지 않는다.
(ⅱ) $Q(x)$의 차수가 $1$일 때
$P(x)$의 차수가 $2$이고 $P(x)+\{ Q(x)\}^{2}$은 상수이다.
$P(x)$, $Q(x)$의 최고차항의 계수를 각각 $p$, $q$라 하자.
$f(x)$의 최고차항의 계수는 $P(x)Q(x)$의최고차항의 계수와 같으므로 $pq = 1$
$P(x)+\{ Q(x)\}^{2}$은 상수이므로 $p+q^{2} = 0$
그러므로 $q^{3} = -1$에서 $q = -1$, $p = -1$
$P(0) = -2$, $Q(0) = 1$이므로
$P(x) = -x^{2}+ax-2$ ($a$는 상수), $Q(x) = -x+1$
$P(x)+\{ Q(x)\}^{2}$은 상수이고
$P(x)+\{ Q(x)\}^{2} = -x^{2}+ax-2+(-x+1)^{2} = (a-2)x-1$
이므로 $a=2$에서 $P(x) = -x^{2}+2x-2$
그러므로 $f(x) = (-x^{2}+2x-2)(-x+1)-1$
(ⅲ) $Q(x)$가 $0$이 아닌 상수일 때
$P(x)$의 차수가 $3$이므로 $P(x)+\{ Q(x)\}^{2}$의 차수가 $3$이 되어 ㉠을 만족시키지 않는다.
(ⅰ), (ⅱ), (ⅲ)에 의하여 $f(2) = 1$
20. $0$이 아닌 실수 $a$에 대하여 좌표평면 위의 서로 다른 세 점 $\mathrm{A}(2a, 0)$, $\mathrm{B}$, $\mathrm{C}$가 다음 조건을 만족시킨다.
∘ 삼각형 $\mathrm{ABC}$의 무게중심의 좌표는 $(0, 2)$이다.
∘ $\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$
다음은 $\overline{\mathrm{BC}} = 2\sqrt{a^{2}+1}$일 때, 점 $\mathrm{B}$의 $x$좌표와 $y$좌표의 합을 구하는 과정이다. (단, 점 $\mathrm{B}$의 $x$좌표는 점 $\mathrm{C}$의 $x$좌표보다 크다.)
선분 $\mathrm{BC}$의 중점을 $\mathrm{M}(b, c)$, 삼각형 $\mathrm{ABC}$의 무게중심을 $\mathrm{G}$라 하면, 점 $\mathrm{G}(0, 2)$는 선분 $\mathrm{AM}$을 $2 : 1$로 내분하는 점이므로 $b = -a$, $c = \fbox{ $\textbf{(가)}$ }$이다.
$\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$이고 직선 $\mathrm{AM}$의 기울기가 $-\dfrac{1}{a}$이므로
직선 $\mathrm{BC}$의 방정식은
$y = \fbox{ $\textbf{(나)}$ } \times \{ x-(-a) \} + \fbox{ $\textbf{(가)}$ }$
이다.
점 $\mathrm{B}$의 $x$좌표를 $k$라 하면
점 $\mathrm{B}$의 $y$좌표는 $\fbox{ $\textbf{(나)}$ }\times (k+a) + \fbox{ $\textbf{(가)}$ }$이다.
$\overline{\mathrm{BM}} = \dfrac{1}{2}\overline{\mathrm{BC}}$이고 점 $\mathrm{B}$의 $x$좌표가 점 $\mathrm{C}$의 $x$좌표보다 크므로 $k = \fbox{ $\textbf{(다)}$ }$이다.
따라서 점 $\mathrm{B}$의 $x$좌표와 $y$좌표의 합은 $\fbox{ $\textbf{(라)}$ }$이다.
위의 (가), (라)에 알맞은 수를 각각 $p$, $q$라 하고, (나), (다)에 알맞은 식을 각각 $f(a)$, $g(a)$라 할 때, $f(p)\times g(q)$의 값은? [4점]
① $-10$
② $-\frac{19}{2}$
③ $-9$
④ $-\frac{17}{2}$
⑤ $-8$
③
선분 $\mathrm{BC}$의 중점을 $\mathrm{M}(b, c)$, 삼각형 $\mathrm{ABC}$의 무게중심을 $\mathrm{G}$라 하면, 점 $\mathrm{G}(0, 2)$는 선분 $\mathrm{AM}$을 $2 : 1$로 내분하는 점이므로
$\left( \dfrac{2\times b+1 \times 2a}{2+1}, \dfrac{2\times c+1 \times 0}{2+1} \right)$에서
$2a+2b = 0$, $2c = 6$
$b = -a$, $c = \fbox{ $3$ }$이다.
$\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$이므로 직선 $\mathrm{AM}$과 직선 $\mathrm{BC}$는 서로 수직이고, 직선 $\mathrm{AM}$의 기울기가 $-\frac{1}{a}$이므로 직선 $\mathrm{BC}$의 기울기는 $a$이다.
직선 $\mathrm{BC}$는 기울기가 $a$이고 점 $\mathrm{M}(-a, 3)$을 지나므로 직선 $\mathrm{BC}$의 방정식은
$y = \fbox{ $a$ } \times \{ x-(-a) \} + \fbox{ $3$ }$이다.
점 $\mathrm{B}$의 $y$좌표를 $k$라 하면
점 $\mathrm{B}$는 직선 $\mathrm{BC}$ 위의 점이므로
점 $\mathrm{B}$의 $y$좌표는 $\fbox{ $a$ }\times (k+a) + \fbox{ $3$ }$이다.
$\mathrm{B}(k, a(k+a)+3)$, $\mathrm{M}(-a, 3)$이므로
$\overline{\mathrm{BM}} = \sqrt{(-a-k)^{2}+(3-ak-a^{2}-3)^{2}}$
$= \sqrt{(a+k)^{2}+a^{2}(a+k)^{2}}$
$= \sqrt{(a+k)^{2}(a^{2}+1)}$
이고, $\overline{\mathrm{BM}} = \dfrac{1}{2}\overline{\mathrm{BC}} = \sqrt{a^{2}+1}$이므로
$\sqrt{(a+k)^{2}(a^{2}+1)} = \sqrt{a^{2}+1}$
$\sqrt{(a+k)^{2}} = 1$에서 $|a+k| = 1$이므로
$k = -a+1$ 또는 $k = -a-1$
점 $\mathrm{B}$의 $c$좌표가 점 $\mathrm{C}$의 $x$좌표보다 크므로
점 $\mathrm{B}$의 $x$좌표는 점 $\mathrm{M}$의 $x$좌표보다 크다.
그러므로 $k = \fbox{ $-a+1$ }$이다.
점 $\mathrm{B}$의 $y$좌표는 $a(-a+1)+a^{2}+3 = a+3$이므로
점 $\mathrm{B}$의 $x$좌표와 $y$좌표의 합은
$(-a+1)+(a+3) = \fbox{ $4$ }$이다.
따라서 $p = 3$, $q = 4$이고
$f(a) = a$, $g(a) = -a+1$이므로
$f(p) \times g(q) = 3 \times (-4+1) = -9$
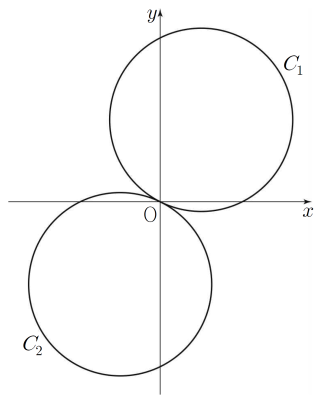
21. 좌표평면 위의 제$1$사분면에 있는 점 $\mathrm{A}$를 중심으로 하고 원점 $\mathrm{O}$를 지나는 원 $C_1$이 있다. 원 $C_1$을 원점 $\mathrm{O}$에 대하여 대칭이동한 원을 $C_2$라 할 때, 두 원 $C_1$, $C_2$가 다음 조건을 만족시킨다.
삼각형 $\mathrm{OPQ}$의 외접원의 중심이 선분 $\mathrm{PQ}$ 위에 있도록 하는 원 $C_1$ 위의 점 $\mathrm{P}$와 원 $C_2$ 위의 점 $\mathrm{Q}$에 대하여 $\overline{\mathrm{PQ}} = 6$이다.
원 $C_2$가 $$x축과 만나는 점 중 $\mathrm{O}$가 아닌 점을 $\mathrm{B}$라 할 때, 원 $C_2$ 위의 점 $\mathrm{B}$에서의 접선을 $l$이라 하자. 직선 $l$의 기울기가 $\dfrac{1}{2}$일 때, 점 $\mathrm{B}$와 직선 $l$ 사이의 거리는? [4점]
① $\frac{3}{5}$
② $\frac{2}{3}$
③ $\frac{11}{15}$
④ $\frac{4}{5}$
⑤ $\frac{13}{15}$
①
삼각형 $\mathrm{OPQ}$의 외접원의 중심이 선분 $\mathrm{PQ}$ 위에 있으려면 삼각형 $\mathrm{OPQ}$는 $\angle \mathrm{POQ} = 90^{\circ}$인 직각삼각형이어야 한다.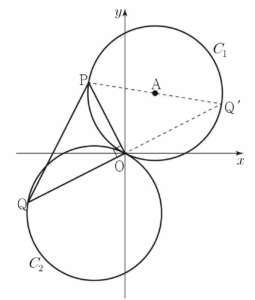
점 $\mathrm{Q}$를 원점 $\mathrm{O}$에 대하여 대칭이동한 점을 $\mathrm{Q’}$이라 하면 점 $\mathrm{Q’}$은 원 $C_1$ 위의 점이고
$\overline{\mathrm{OQ}} = \overline{\mathrm{OQ’}}$, $\angle \mathrm{POQ’} = 180^{\circ} – \angle \mathrm{POQ} = 90^{\circ}$
이므로 두 삼각형 $\mathrm{OPQ}$, $\mathrm{OPQ’}$은 서로 합동이다.
그러므로 $\overline{\mathrm{PQ’}} = \overline{\mathrm{PQ}} = 6$
또한 원 $C_1$은 직각삼각형 $\mathrm{OPQ’}$의 외접원이므로 선분 $\mathrm{PQ’}$은 원 $C_1$의 지름이다.
원 $C_1$의 중심의 좌표를 $\mathrm{A}(a, b)$ ($a \gt 0$, $b \gt 0$)이라 하면 원 $C_1$이 원점을 지나므로
$\sqrt{a^{2}+b^{2}} = 3$, $a^{2}+b^{2} = 9$ $\cdots\cdots$ ㉠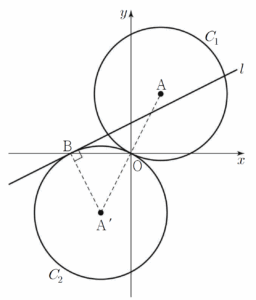
원 $C_2$의 중심을 $\mathrm{A’}$이라 하면 점 $\mathrm{A’}$은 점 $\mathrm{A}$를 원점 $\mathrm{O}$에 대하여 대칭이동한 점이므로 점 $\mathrm{A’}$의 좌표는 $(-a, -b)$이다.
원 $C_2$의 방정식은 $(x+a)^{2}+(y+b)^{2} = a^{2}+b^{2}$이므로 점 $\mathrm{B}$의 좌표는 $(-2a, 0)$
직선 $l$의 기울기는 $\frac{1}{2}$이고 직선 $l$과 직선 $\mathrm{BA’}$이 서로 수직이므로 직선 $\mathrm{BA’}$의 기울기는 $-2$이다.
$\frac{-b-0}{-a-(-2a)} = -\frac{b}{a} = -2$에서 $b = 2a$ $\cdots\cdots$ ㉡
㉠, ㉡에서 $a = \frac{3}{5}\sqrt{5}$, $b = \frac{6}{5}\sqrt{5}$
직선 $j$의 방정식은 $y = \frac{1}{2}(x+\frac{6}{5}\sqrt{5})$
즉, $5x-10y+6\sqrt{5} = 0$
따라서 점 $\mathrm{A}(\frac{3}{5}\sqrt{5}, \frac{6}{5}\sqrt{5})$와 직선 $l$ 사이의 거리는 $\dfrac{|\,3\sqrt{5}-12\sqrt{5}+6\sqrt{5}\,|}{\sqrt{5^{2}+(-10)^{2}}} = \dfrac{3}{5}$
24. 두 행렬 $A = \begin{pmatrix} 4 & 3 \\ 3 & 4 \end{pmatrix}$, $B = \begin{pmatrix} 8 & 2 \\ 2 & 8 \end{pmatrix}$에 대하여 $pA-B = q\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix}$일 때, $p+q$의 값을 구하시오. (단, $p$와 $q$는 상수이다.) [3점]
$6$
$pA-B = \begin{pmatrix} 4p & 3p \\ 3p & 4p \end{pmatrix}-\begin{pmatrix} 8 & 2 \\ 2 & 8 \end{pmatrix} = \begin{pmatrix} 4p-8 & 3p-2 \\ 3p-2 & 4p-8 \end{pmatrix}$
이고 $q\begin{pmatrix} 0 & 1 \\ 1 & 0 \end{pmatrix} = \begin{pmatrix} 0 & q \\ q & 0 \end{pmatrix}$이므로
$4p-8 = 0$에서 $p = 2$,
$3p-2$ = q에서 $q = 4$
따라서 $p+q = 6$
25. $1$부터 $6$까지의 자연수가 하나씩 적혀 있는 $6$장의 카드가 있다. 이 $6$장의 카드를 모두 한 번씩 사용하여 일렬로 나열할 때, 양 끝에 놓인 카드에 적힌 두 수의 곱이 홀수가 되도록 나열하는 경우의 수를 구하시오. [3점]
26. $x$에 대한 사차방정식 $(2x^{2}+kx)^{2}+10(2x^{2}+kx)+16 = 0$의 서로 다른 실근의 개수가 $2$가 되도록 하는 모든 자연수 $k$의 값의 합을 구하시오. [4점]
$18$
$2x^{2}+kx = X$라 하면
$(2x^{2}+kx)^{2}+10(2x^{2}+kx)+16 = 0$에서
$X^{2}+10X+16 = 0$, $(X+2)(X+8) = 0$
$(2x^{2}+kx+2)(2x^{2}+kx+8) = 0$
모든 실수 $x$에 대하여
$(2x^{2}+kx+2)-(2x^{2}+kx+8) = -6 \ne 0$이므로
연립방정식
$\begin{cases} 2x^{2}+kx+2 = 0 \\ 2x^{2}+kx+8 = 0 \end{cases}$
의 실근은 존재하지 않는다. $\cdots\cdots$ ㉠
두 이차방정식 $2x^{2}+kx+2 = 0$, $2x^{2}+kx+8 = 0$의 판별식을 각각 $D_1$, $D_2$라 하면
$D_1 = k^{2}=4\times 2\times 2 = k^{2}-16$,
$D_2 = k^{2}=4\times 2\times 8 = k^{2}-64$
이므로 $D_{1} \gt D_2$
㉠에 의하여 사차방정식
$(2x^{2}+kx)^{2}+10(2x^{2}+kx)+16 = 0$의 서로 다른 실근의 개수가 $2$이기 위해서는
$D_1 \gt 0$, $D_2 \lt 0$이어야 한다.
$D_1 = k^{2}-16 \gt 0$에서 $k \lt -4$ 또는 $k \gt 4$,
$D_2 = k^{2}-64 \lt 0$에서 $-8 \lt k \lt 8$
그러므로 $-8 \lt k \lt -4$ 또는 $4 \lt k \lt 8$
따라서 구하는 모든 자연수 $k$의 값의 합은
$5+6+7 = 18$
27. 상수 $k$에 대하여 $x$에 대한 이차방정식 $x^{2}+kx-\dfrac{1}{2}k^{2}+3k = 0$이 서로 다른 두 실근 $\alpha$, $\beta$를 갖는다. $\alpha^{2}-k\beta = 12$일 때, $\alpha^{2}+\beta^{2}$의 값을 구하시오. [4점]
$20$
이차방정식 $x^{2}+kx-\frac{1}{2}k^{2}+3k = 0$이 서로 다른 두 실근을 가지므로 이차방정식 $x^{2}+kx-\frac{1}{2}k^{2}+3k = 0$의 판별식을 $D$라 하면
$D = k^{2}-4(-\frac{1}{2}k^{2}+3k) = 3k(k-4) \gt 0$
$k \lt 0$ 또는 $k \gt 4$ $\cdots\cdots$ ㉠
이차방정식의 근과 계수의 관계에 의하여
$\alpha+\beta = -k$, $\alpha \beta = -\frac{1}{2}k^{2}+3k$
또한 $\alpha$는 이차방정식 $x^{2}+kx-\frac{1}{2}k^{2}+3k = 0$의 한 근이므로
$\alpha^{2}+k\alpha-\frac{1}{2}k^{2}+3k = 0$에서 $\alpha^{2} = -k\alpha+\frac{1}{2}k^{2}-3k$
$\alpha^{2}-k\beta = -k\alpha+\frac{1}{2}k^{2}-3k-k\beta$
$= -k(\alpha+\beta)+\frac{1}{2}k^{2}-3k$
$= k^{2}+\frac{1}{2}k^{2}-3k$
$= \frac{3}{2}k^{2}-3k$ $= 12$
에서 $\frac{3}{2}k^{2}-3k-12 = 0$, $(k+2)(k-4) = 0$
㉠에 의하여 $k = -2$
$\alpha+\beta = 2$, $\alpha \beta = -8$
따라서 $\alpha^{2}+\beta^{2} = (\alpha+\beta)^{2}-2\alpha \beta$
$= 2^{2}-2\times (-8) = 20$
28. 원 $O$가 $x$축과 두 점 $\mathrm{A}$, $\mathrm{B}$에서 만나고, $y$축과 두 점 $\mathrm{C}$, $\mathrm{D}$에서 만난다. 네 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$와 원 $O$가 다음 조건을 만족시킬 때, 사각형 $\mathrm{ABCD}$의 넓이를 구하시오. (단, 점 $\mathrm{A}$의 $x$좌표는 점 $\mathrm{B}$의 $x$좌표보다 작고, 점 $\mathrm{C}$의 $y$좌표는 점 $\mathrm{D}$의 $y$좌표보다 작다.) [4점]
(가) 선분 $\mathrm{AB}$를 $1 : 4$로 내분하는 점은 선분 $\mathrm{CD}$의 중점이다.
(나) 원 $O$가 직선 $4x-3y+13 = 0$에 접한다.
$40$
선분 $\mathrm{AB}$는 $x$축 위에 있으므로 선분 $\mathrm{AB}$를 $1 : 4$로 내분하는 점은 $x$축 위의 점이고, 선분 $\mathrm{CD}$는 $y$축 위에 있으므로 선분 $\mathrm{CD}$의 중점은 $y$축 위의 점이다.
$x$축 위에 있고 동시에 $y$축 위에 있는 점은 원점 $\mathrm{O}$뿐이므로 $\overline{\mathrm{AO}} : \overline{\mathrm{BO}} = 1 : 4$, $\overline{\mathrm{CO}} = \overline{\mathrm{DO}}$이다.
직선 $\mathrm{AB}$는 선분 $\mathrm{CD}$의 수직이등분선이므로 선분 $\mathrm{AB}$는 원 $O$의 지름이다.
점 $\mathrm{O}$는 두 점 $\mathrm{A}$, $\mathrm{B}$를 $1 : 4$로 내분하는 점이므로 점 $\mathrm{A}$의 좌표를 $\mathrm{A}(-a, 0)$ ($a \gt 0$)이라 하면 점 $\mathrm{B}$의 좌표는 $\mathrm{B}(4a, 0)$이다.
선분 $\mathrm{AB}$가 원 $O$의 지름이므로 원 $O$의 중심의 좌표는 $(\frac{3}{2}a, 0)$이고 반지름의 길이는 $\frac{5}{2}a$이다.
조건 (나)에 의하여 원 $O$의 중심 $(\frac{3}{2}a, 0)$과 직선 $4x-3y+13 = 0$ 사이의 거리는 $\frac{5}{2}a$이다.
$\frac{|6a+13|}{\sqrt{4^{2}+(-3)^{2}}} = \frac{5}{2}a$, $|6a+13| = \frac{25}{2}a$에서
$a = 2$이므로 $\mathrm{A}(-2, 0)$, $\mathrm{A}(8, 0)$이고 원 $O$의 방정식은 $(x-3)^{2}+y^{2} = 25$이다.
두 점 $\mathrm{C}$, $\mathrm{D}$는 원 $O$와 $y$축과의 교점이므로 $9+y^{2} = 25$에서 $y = -4$ 또는 $y = 4$
그러므로 $\mathrm{C}(0, -4)$, $\mathrm{D}(0, 4)$이다.
따라서 사각형 $\mathrm{ACBD}$의 넓이는
$\frac{1}{2}\times \overline{\mathrm{AB}}\times \overline{\mathrm{CD}} = \frac{1}{2} \times 10 \times 8 = 40$
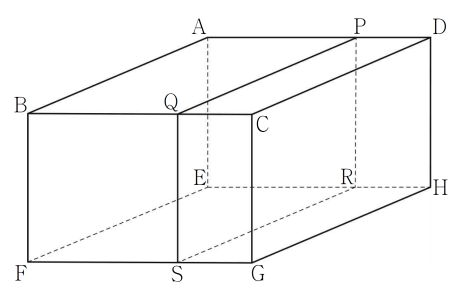
29. 그림과 같이 정사각형 $\mathrm{ABCD}$를 밑면으로 하는 직육면체 $\mathrm{ABCD}-\mathrm{EFGH}$가 있다. 선분 $\mathrm{AD}$ 위의 점 $\mathrm{P}$와 선분 $\mathrm{BC}$ 위의 점 $\mathrm{Q}$를 $\overline{\mathrm{AP}} = \overline{\mathrm{BQ}} = \overline{\mathrm{BF}}$가 되도록 잡고, 점 $\mathrm{P}$에서 선분 $\mathrm{EH}$에 내린 수선의 발을 $\mathrm{R}$, 점 $\mathrm{Q}$에서 선분 $\mathrm{FG}$에 내린 수선의 발을 $\mathrm{S}$라 하자.
직육면체 $\mathrm{ABCD}-\mathrm{EFGH}$의 부피를 $V_1$, 직육면체 $\mathrm{ABQP}-\mathrm{EFSR}$의 부피를 $V_2$라 하자.
$$(\overline{\mathrm{AB}} + \overline{\mathrm{BF}}) \times \overline{\mathrm{SD}}^{\,2}, \:V_{1}+V_{2} = \frac{15}{4}$$
일 때, $(\overline{\mathrm{AB}} + \overline{\mathrm{BF}})^{3} = \dfrac{q}{p}$이다. $p+q$의 값을 구하시오.
(단, $\overline{\mathrm{AB}} \gt \overline{\mathrm{BF}}$이고, $p$와 $q$는 서로소인 자연수이다.) [4점]
$133$
$\overline{\mathrm{AB}} = a$, $\overline{\mathrm{BF}} = b$ ($a \gt b$)라 하자.
직사각형 $\mathrm{RSGH}$에서 $\overline{\mathrm{SG}} = a-b$, $\overline{\mathrm{GH}} = a$이므로
$\overline{\mathrm{SH}}^{2} = \overline{\mathrm{SG}}^{2}+\overline{\mathrm{GH}}^{2}$
$= (a-b)^{2}+a^{2}$
$= 2a^{2}-2ab+b^{2}$
직각삼각형 $\mathrm{DHS}$에서
$\overline{\mathrm{SD}}^{2} = \overline{\mathrm{SH}}^{2}+\overline{\mathrm{DH}}^{2}$
$= (2a^{2}-2ab+b^{2})+b^{2}$
$= 2(a^{2}-ab+b^{2})$
이므로
$(\overline{\mathrm{AB}} + \overline{\mathrm{BF}}) \times \overline{\mathrm{SD}}^{2}$ $= (a+b)\times 2(a^{2}-ab+b^{2})$
$= 2(a^{3}+b^{3}) = \frac{35}{4}$
에서 $a^{3}+b^{3} = \frac{35}{8}$
$V_{1} = \overline{\mathrm{AB}} \times \overline{\mathrm{BC}} \times\overline{\mathrm{BF}} = a^{2}b$,
$V_{2} = \overline{\mathrm{AB}} \times \overline{\mathrm{BQ}} \times\overline{\mathrm{BF}} = ab^{2}$
이므로 $V_{1}+V_{2} = a^{2}b+ab^{2} = \frac{15}{4}$
$(\overline{\mathrm{AB}} + \overline{\mathrm{BF}})^{3}$ $= (a+b)^{3}$
$= a^{3}+3a^{2}b+3ab^{2}+b^{3}$
$= a^{3}+b^{3}+3(a^{2}b+ab^{2}) = \frac{35}{8}+\frac{45}{4} = \frac{125}{8}$
이므로 $p = 8$, $q = 125$
따라서 $p+q = 133$
30. 두 상수 $p$ ($p \gt 0$), $q$에 대하여 이차함수 $f(x) = \dfrac{1}{2}(x-p)^{2}+q$가 있다. 함수 $f(x)$와 양수 $m$에 대하여 함수 $g(x)$를 $$g(x) = -f(x-m)$$ 이라 할 때, 방정식 $f(x) = g(x)$가 서로 다른 두 실근 $\alpha$, $\beta$ ($\alpha \lt \beta$)를 갖는다. 함수 $h(x)$를 $$h(x) = \begin{cases} f(x) & (x \le \alpha \textbf{ 또는 } x \ge \beta) \\ g(x) & (\alpha \lt x \lt \beta) \end{cases}$$ 라 할 때, 함수 $h(x)$는 다음 조건을 만족시킨다.
$x$에 대한 방정식 $h(x) = t$의 서로 다른 실근의 개수가 $2$ 이상이면서 서로 다른 모든 실근의 합이 $4p+2m$이 되도록 하는 모든 실수 $t$의 값의 범위는 $g(p) \lt t \lt 5$이다.
$f(m)+g(m) = -4$일 때, $m \times (p-q)$의 값을 구하시오. [4점]
$16$
$q \ge 0$이면 모든 실수 $x$에 대하여 $f(x) \ge 0$, $g(x) \le 0$이 되어 방정식 $f(x) = g(x)$는 서로 다른 두 실근을 갖지 않으므로 $q \lt 0$
방정식 $f(x) = g(x)$가 서로 다른 두 실근 $\alpha$, $\beta$를 가지므로 두 함수 $y = f(x)$, $y = g(x)$의 그래프는 서로 다른 두 점 $\mathrm{P}(\alpha, f(\alpha))$, $\mathrm{Q}(\beta, f(\beta))$에서 만난다.
(ⅰ) $\alpha \ge p$일 때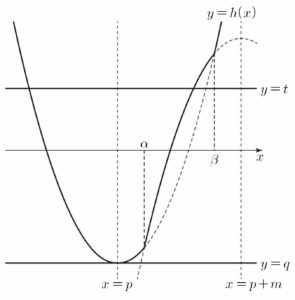 
$t \gt q$인 모든 실수 $t$에 대하여 방정식 $h(x) = t$의 서로 다른 실근의 개수는 $2$이다. $t \gt q$인 실수 $t$에 대하여함수 $y = h(x)$의 그래프와 직선 $y = t$가 만나는 두 교점의 $x$좌표를 $x_1$, $x_2$,
함수 $y = f(x)$의 그래프와 직선 $y = t$가 만나는 두 교점의 $x$좌표를 $x_3$, $x_4$라 하자.
이때 $t \gt q$인 모든 실수 $t$에 대하여 함수 $y = f(x)$의 그래프와 직선 $y = t$가 만나는 두 교점의 $x$좌표의 합은 $2p$이므로 방정식 $h(x) = t$의 서로 다른 두 실근의 합 $x_{1}+x_2$는 $x_{1}+x_{2} \le x_{3}+x_{4} = 2p$
$p \gt 0$, $m \gt 0$이므로 $x_{1}+x_2$는 $x_{1}+x_{2} \lt 4p + 2m$이 되어 조건을 만족시키지 않는다.
(ⅱ) $\alpha \lt p$일 때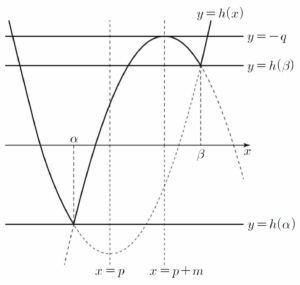
$h(\alpha) \lt t \lt h(\beta)$ 또는 $t \gt -q$인 모든 실수 $t$에 대하여 방정식 $h(x) = t$의 서로 다른 실근의 개수는 $2$이고,
$t = h(\beta)$ 또는 $t = -q$인 실수 $t$에 대하여 방정식 $h(x) = t$의 서로 다른 실근의 개수는 $3$이고,
$h(\beta) \lt t \lt -q$인 모든 실수 $t$에 대하여 방정식 $h(x) = t$의 서로 다른 실근의 개수는 $4$이다.
(a) $h(\alpha) \lt t \lt h(\beta)$ 또는 $t \gt -q$일 때
(ⅰ)과 같은 방법으로 구하면 방정식 $h(x) = t$의 서로 다른 두 실근의 합은 $2p$보다 작거나 같으므로 조건을 만족시키지 않는다.
(b) $t = h(\beta)$ 또는 $t = -q$일 때
(ⅰ)과 같은 방법으로 구하면 방정식 $h(x) = t$의 서로 다른 세 실근의 합은 $3p+m$보다 작거나 같으므로 조건을 만족시키지 않는다.
(c) $h(\beta) \lt t \lt -q$일 때
함수 $y = h(x)$의 그래프와 직선 $y = t$가 만나는 네 교점의 $x$좌표를 작은 수부터 차례로 $x_{5}$, $x_{6}$, $x_{7}$, $x_{8}$이라 하면
함수 $y = f(x)$의 그래프와 직선 $y = t$가 만나는 두 교점의 $x$좌표는 $x_{5}$, $x_{8}$이고
함수 $y = g(x)$의 그래프와 직선 $y = t$가 만나는 두 교점의 좌표는 $x_{6}$, $x_{7}$이다.
이때 $x_{5}+x_{8} = 2p$, $x_{6}+x_{7} = 2p+m$이므로 방정식 $h(x) = t$의 서로 다른 네 실근의 합 $x_{5}+x_{6}+x_{7}+x_{8}$은 $x_{5}+x_{6}+x_{7}+x_{8} = 4p+2m$
그러므로 조건을 만족시키는 모든 실수 $t$의 값의 범위는 $h(\beta) \lt t \lt -q$
조건에 의하여 $h(\beta) = g(p)$이고 $-q = 5$, $q = -5$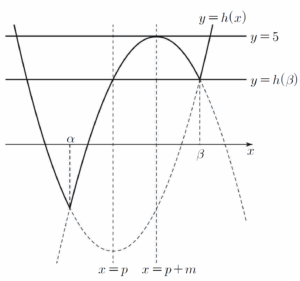
이때 $h(\beta) = f(\beta) = g(\beta)$이므로 $g(p) = f(\beta)$
이차함수 $y = g(x)$의 그래프는직선 $x = p+m$에 대하여 대칭이므로
$p+\beta = 2(p+m)$, $\beta = p+2m$
$f(\beta) = f(p+2m)$ $= \frac{1}{2}(2m)^{2}-5 = 2m^{2}-5$
이고
$g(p) = -\frac{1}{2}(2m)^{2}+5 = -\frac{1}{2}m^{2}+5$
이므로 $2m^{2}-5 = -\frac{1}{2}m^{2}+5$에서 $m^{2} = 4$, $m = 2$
그러므로 $f(x) = \frac{1}{2}(x-p)^{2}-5$,
$g(x) = -\frac{1}{2}(x-2-p)^{2}+5$
$f(m)+g(m) = f(2)+g(2)$
$= \{ \frac{1}{2}(2-p)^{2}-5 \}+(-\frac{1}{2}p^{2}+5)$ $= -2p+2$
$-2p+2 = -4$이므로 $p = 3$
(ⅰ), (ⅱ)에 의하여
$m \times (p-q) = 2 \times \{ 3-(-5) \} = 16$