적분
람다 $\lambda$의 차례
부정적분
1. 부정적분
(1) 부정적분
함수 $F(x)$의 도함수가 $f(x)$일 때, 즉 $F^{\prime}(x) = f(x)$일 때 $F(x)$들 전체를 $f(x)$의 부정적분이라 하고, 기호로 $\displaystyle \int f(x) dx$와 같이 나타냅니다.
(2) 함수 $f(x)$의 부정적분 중 하나를 $F(x)$라 하면 $$\int f(x) dx = F(x) + C$$입니다. 이때 $C$를 적분상수라고 합니다.
2. 부정적분과 미분의 관계
함수 $f(x)$에 대하여
① $\displaystyle \frac{d}{dx} \int f(x) dx = f(x)$
② $\displaystyle \int \left\{ \frac{d}{dx}f(x) \right\}dx = f(x) + C$ (단, $C$는 적분상수)
부정적분의 계산
1. 함수 $y = x^{n}$의 부정적분
① $n$이 양의 정수일 때 $$\int x^{n} dx = \frac{1}{n+1}x^{n+1} + C \: \textbf{(단, }C\textbf{는 적분상수)}$$
② $\displaystyle \int 1 dx = x + C$ (단, $C$는 적분상수)
$\displaystyle \int 1 dx$를 간단히 $\displaystyle \int dx$로 나타내기도 합니다.
2. 함수의 실수배, 합, 차의 부정적분
두 함수 $f(x)$, $g(x)$에 대하여
① $\int k f(x) dx = k \int f(x) dx$ (단, $k$는 $0$이 아닌 실수)
② $\int \{ f(x) + g(x) \}dx = \int f(x) dx + \int g(x) dx$
③ $\int \{ f(x) -\, g(x) \}dx = \int f(x) dx -\, \int g(x) dx$
정적분
1. 정적분의 정의
(1) 함수 $f(x)$가 두 실수 $a$, $b$를 포함하는 구간에서 연속일 때, $f(x)$의 한 부정적분을 $F(x)$라 하면 $x$의 값이 $a$에서 $b$까지 변할 때의 $F(x)$의 변화량 $F(b) -\, F(a)$를 함수 $f(x)$의 $a$에서 $b$까지의 정적분이라 하고, 기호로 다음과 같이 나타냅니다. $$\int_{a}^{b}f(x) dx = \Bigg[ F(x) \Bigg]_{a}^{b} = F(b) -\, F(a)$$
① 정적분 $\int_{a}^{b}f(x) dx$의 값을 구하는 것을 함수 $f(x)$를 $a$에서 $b$까지 적분한다고 하고 $a$를 아래끝, $b$를 위끝이라고 합니다. 이때 $a$부터 $b$까지를 적분구간이라고 합니다.
② 정적분에서 변수를 $x$ 대신 다른 문자를 사용해도 그 값은 변하지 않습니다. 즉 $\int_{a}^{b}f(x) dx = \int_{a}^{b}f(t) dt = \int_{a}^{b}f(u) du$
③ 부정적분 $\int f(x) dx$은 함수들의 집합이지만 정적분 $\int_{a}^{b}f(x) dx$은 실수입니다.
(2) 함수 $f(x)$가 두 실수 $a$, $b$를 포함하는 구간에서 연속일 때, 다음이 성립합니다.
① $\int_{a}^{a}f(x) dx = 0$
② $\int_{a}^{b}f(x) dx = – \int_{b}^{a}f(x) dx$
2. 정적분과 미분의 관계
함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, $$\frac{d}{dx} \int_{a}^{x} f(t) dt = f(x) \: (\textbf{단, } a \lt x \lt b)$$
즉, $f(x)$의 부정적분 중 하나의 함수가 $\int_{a}^{x} f(t) dt$입니다.
3. 정적분의 성질
두 함수 $f(x)$, $g(x)$가 임의의 실수 $a$, $b$, $c$를 포함하는 구간에서 연속일 때
① $\int_{a}^{b} k f(x) dx = k \int_{a}^{b} f(x) dx$ (단, $k$는 실수)
② $\int_{a}^{b} \{ f(x) + g(x) \}dx = \int_{a}^{b} f(x) dx + \int_{a}^{b} g(x) dx$
③ $\int_{a}^{b} \{ f(x) -\, g(x) \}dx = \int_{a}^{b} f(x) dx -\, \int_{a}^{b} g(x) dx$
④ $\int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx$
4. 정적분 $\displaystyle \int_{-a}^{a}x^{n}dx$의 계산
$n$이 자연수일 때 $\int_{-a}^{a}x^{n}dx$에 대하여 다음이 성립합니다.
① $n$이 짝수일 때, $\int_{-a}^{a}x^{n}dx = 2 \int_{0}^{a}x^{n}dx = 2 \int_{-a}^{0}x^{n}dx$
② $n$이 홀수일 때, $\int_{-a}^{a}x^{n}dx = 0$
5. 정적분으로 정의된 함수
(1) 정적분으로 정의된 함수의 미분
① $\displaystyle \frac{d}{dx} \int_{a}^{x} f(t) dt = f(x)$ (단, $a$는 실수)
② $\displaystyle \frac{d}{dx} \int_{x}^{x+a} f(t) dt = f(x+a) -\, f(x)$ (단, $a$는 실수)
(2) 정적분으로 정의된 함수의 극한
① $\displaystyle \lim_{x \to 0}\frac{1}{x} \int_{a}^{x+a} f(t) dt = f(a)$
② $\displaystyle \lim_{x \to 0}\frac{1}{x -a} \int_{a}^{x} f(t) dt = f(a)$
넓이
1. 곡선과 $x$축 사이의 넓이
(1) 정적분의 기하적 의미
함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속이고 $f(x) \ge 0$일 때, 정적분 $\displaystyle \int_{a}^{b} f(x) dx$는 곡선 $y = f(x)$와 $x$축 및 두 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이와 같습니다.
(2) 곡선과 $x$축 사이의 넓이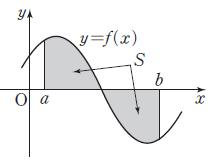
함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 곡선 $y = f(x)$와 $x$축 및 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{a}^{b}|\,f(x)\,| dx$$
① 닫힌구간 $[\,a, \,b\,]$에서 $f(x)$의 값이 양수인 경우와 음수인 경우가 모두 있을 때에는 $f(x)$의 값이 양수인 구간과 음수인 구간으로 나누어서 넓이 $S$를 구해야 합니다.
② 포물선 $y = a(x -\,\alpha)(x -\,\beta)$ ($a \ne 0$, $\alpha \lt \beta$)와 $x$축으로 둘러싸인 도형의 넓이 $S$는 $S = \int_{\alpha}^{\beta}|a(x -\,\alpha)(x -\,\beta)| dx = \dfrac{|a|(\beta -\,\alpha)^{3}}{6}$
2. 두 곡선 사이의 넓이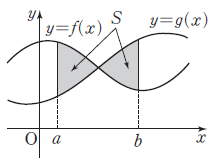
두 함수 $f(x)$, $g(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 두 곡선 $y = f(x)$, $y = g(x)$ 및 두 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{a}^{b}|\,f(x) -\, g(x)\,| dx$$
속도와 거리
1. 수직선 위를 움직이는 점의 위치와 움직인 거리
수직선 위를 움직이는 점 $\mathrm{P}$의 시각 $t$에서의 속도가 $v(t)$, 시각 $t = a$에서의 위치가 $x_{0}$일 때
① 시각 $t$에서의 점 $\mathrm{P}$의 위치 $x$는 $x = x_{0} +\int_{a}^{t} v(t) dt$
② 시각 $t = a$에서 $t = b$까지 점 $\mathrm{P}$의 위치의 변화량은 $\int_{a}^{b} v(t) dt$
③ 시각 $t = a$에서 $t = b$까지 점 $\mathrm{P}$가 움직인 거리 $s$는 $s = \int_{a}^{b} |\,v(t)\,|dt$
