경우의 수
람다 $\lambda$의 차례
원순열
1. 원순열
(1) 원순열
서로 다른 것을 원형으로 배열하는 순열을 원순열이라 합니다.
(2) 원순열의 수
서로 다른 $n$개를 원형으로 배열하는 원순열의 수는 $$\frac{n!}{n} = (n -\,1)!$$ 여기서 회전하여 일치하는 것은 같은 것으로 보는겁니다.
중복순열과 같은 것이 있는 순열
1. 중복순열
(1) 중복순열
중복을 허용하여 만든 순열을 중복순열이라 하고, 서로 다른 $n$개에서 중복을 허용하여 $r$개를 택하는 중복순열의 수를 기호로 ${}_{n}\Pi_{r}$와 같이 나타냅니다.
(2) 중복순열의 수
서로 다른 $n$개에서 $r$개를 택하는 중복순열의 수는 $${}_{n}\Pi_{r} = n^{r}$$
(3) 중복 허용
① 서로 다른 $n$개에서 중복을 허용하여 $r$개를 택한 후 일렬로 나열할 때, 첫 번째, 두 번째, 세 번째, $\cdots$, $r$번째에 올 수 있는 경우는 각각 $n$가지씩이므로 곱의 법칙에 의하여 ${}_{n}\Pi_{r} = n^{r} = \underbrace{n\cdot n\cdot n\cdots n}_{r\textbf{개}} = n^{r}$
② ${}_{n}\mathrm{P}_{r}$에서는 $0 \le r \le n$이어야 하지만 ${}_{n}\Pi_{r}$에서는 중복하여 택할 수 있으므로 $r \gt n$일 수도 있습니다.
2. 같은 것이 있는 순열
(1) 같은 것이 있는 순열
$n$개 중에서 같은 것이 각각 $p$개, $q$개, $\cdots$, $r$개씩 있을 때, $n$개를 일렬로 나열하는 경우의 수는 $$\frac{n!}{p! q! \cdots r!}\:(\textbf{단, }p + q \cdots + r = n)$$
(2) 최단 거리로 가는 경우의 수
오른쪽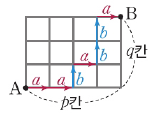
그림과 같은 도로망에서 $\mathrm{A}$에서 $\mathrm{B}$까지 최단 거리로 가려면 오른쪽으로 $p$칸, 위쪽으로 $q$칸 이동해야 합니다. 이때 오른쪽으로 $1$칸 이동하는 것을 $a$, 위쪽으로 $1$칸 이동하는 것을 $b$라 하면 $\mathrm{A}$에서 $\mathrm{B}$까지 최단 거리로 가는 경우의 수는 $\underbrace{a,\, a,\, \cdots,\, a}_{p\textbf{개}},\,\underbrace{b,\, b,\, \cdots,\, b}_{q\textbf{개}}\,$를 일렬로 나열하는 경우의 수와 같으므로 $\dfrac{(p + q)!}{p! q!}$입니다.
중복조합
1. 중복조합
(1) 중복조합
중복을 허용하여 만든 조합을 중복조합이라 하고, 서로 다른 $n$개에서 중복을 허용하여 $r$개를 택하는 중복조합의 수를 기호로 ${}_{n}\mathrm{H}_{r}$와 같이 나타냅니다.
(2) 중복조합의 수
서로 다른 $n$개에서 $r$개를 택하는 중복조합의 수는 $${}_{n}\mathrm{H}_{r} = {}_{n+r-1}\mathrm{C}_{r}$$
(3) 중복 허용
① ${}_{n}\mathrm{C}_{r}$에서는 $0 \le r \le n$이어야 하지만 ${}_{n}\mathrm{H}_{r}$에서는 중복하여 택할 수 있으므로 $r \gt n$일 수도 있습니다.
② 방정식 $x_{1} + x_{2} + \cdots + x_{n} = r\,$ ($n$, $r$은 자연수)에서 $x_{1}$, $x_{2}$, $\cdots$, $x_{n}$이 모두 음이 아닌 정수인 해의 개수는 ${}_{n}\mathrm{H}_{r}$입니다.
2. 순열, 중복순열, 조합, 중복조합의 비교
두 집합 $X = \{1, 2, \cdots, r \}$, $Y = \{1, 2, \cdots, n \}$에 대하여 $X$에서 $Y$로의 함수 $f$ 중에서
① 함수 $f$의 개수: ${}_{n}\Pi_{r}$
② 일대일함수의 개수($r \le n$): ${}_{n}\mathrm{P}_{r}$
③ 증가함수의 개수($r \le n$): ${}_{n}\mathrm{C}_{r}$
감소함수의 개수($r \le n$): ${}_{n}\mathrm{C}_{r}$
④ 감소하지 않는 함수의 개수: ${}_{n}\mathrm{H}_{r}$
증가하지 않는 함수의 개수: ${}_{n}\mathrm{H}_{r}$
여기서 감소하지 않는 함수 $f$는 $X$의 원소 $x_{1}$, $x_{2}$에 대하여 $x_{1} \lt x_{2}$이면 $f(x_{1}) \le f(x_{2})$인 함수이고, 증가하지 않는 함수 $f$는 $x_{1} \lt x_{2}$이면 $f(x_{1}) \ge f(x_{2})$인 함수입니다.
이항정리
1. 이항정리
자연수 $n$에 대하여 $(a+b)^{n}$의 전개식은 다음과 같고, 이것을 이항정리라고 합니다. $$(a+b)^{n} = {}_{n}\mathrm{C}_{0}a^{n} + {}_{n}\mathrm{C}_{1}a^{n-1}b^{1} + \cdots + {}_{n}\mathrm{C}_{r}a^{n-r}b^{r} + \cdots + {}_{n}\mathrm{C}_{n}b^{n}$$ $$= \sum_{r = 0}^{n}a^{n-r}b^{r}$$ 이때 $(a+b)^{n}$의 전개식에서 각 항의 계수 ${}_{n}\mathrm{C}_{0}$, ${}_{n}\mathrm{C}_{1}$, $\cdots$, ${}_{n}\mathrm{C}_{r}$, $\cdots$, ${}_{n}\mathrm{C}_{n}$을 이항계수라 하고, ${}_{n}\mathrm{C}_{r}a^{n-r}b^{r}$을 $(a+b)^{n}$의 전개식의 일반항이라 합니다.
2. 이항계수의 성질
(1) ${}_{n}\mathrm{C}_{0} + {}_{n}\mathrm{C}_{1} + {}_{n}\mathrm{C}_{2} + \cdots + {}_{n}\mathrm{C}_{n} = 2^{n}$
(2) ${}_{n}\mathrm{C}_{0} -\, {}_{n}\mathrm{C}_{1} + {}_{n}\mathrm{C}_{2} -\, \cdots + (-1)^{n}{}_{n}\mathrm{C}_{n} = 2^{n}$
(3) ${}_{n}\mathrm{C}_{0} + {}_{n}\mathrm{C}_{2} + {}_{n}\mathrm{C}_{4} + \cdots = {}_{n}\mathrm{C}_{1} + {}_{n}\mathrm{C}_{3} + {}_{n}\mathrm{C}_{5} + \cdots= 2^{n-1}$
3. 파스칼의 삼각형
자연수 $n$의 값이 $1$, $2$, $3$, $4$, $\cdots\,$일 때, $(a + b)^{n}$의 전개식에서 이항계수를 다음과 같이 배열하고 가장 위쪽에 자연수 $1$을 놓아 삼각형 모양으로 배열한 것을 파스칼의 삼각형이라고 합니다.
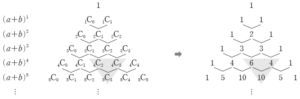① 각 단계의 양끝에 있는 수는 모두 $1$입니다. ${}_{n}\mathrm{C}_{0} = 1$, ${}_{n}\mathrm{C}_{n} = 1$
② 각 단계의 수의 배열은 좌우 대칭입니다. ${}_{n}\mathrm{C}_{r} = {}_{n}\mathrm{C}_{n-r}$
③ 각 단계에서 이웃하는 두 수의 합은 그 다음 단계에서 그 두 수의 중앙에 있는 수와 같습니다. (위에 있는 파스칼의 삼각형에서 회색의 작은 삼각형 부분) ${}_{n-1}\mathrm{C}_{r-1} + {}_{n-1}\mathrm{C}_{r} = {}_{n}\mathrm{C}_{r}$