22년 11월 고2 교육청
4. 함수 $f(x)$가 모든 실수 $x$에 대하여 $$2x+1 \le f(x) \le (x+1)^2$$ 을 만족시킬 때, $\displaystyle \lim_{x \to 0}(x+5)f(x)$의 값은? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
5. $0 \le x \le 3 \pi$일 때, 방정식 $\sqrt{2} \cos x-1 = 0$의 모든 해의 합은? [3점]
① $\frac{15}{4}\pi$
② $4\pi$
③ $\frac{17}{4}\pi$
④ $\frac{9}{2}\pi$
⑤ $\frac{19}{4}\pi$
6. 함수 $f(x)$에 대하여 $\displaystyle \lim_{x \to \infty}\frac{f(x)}{x} = 3$일 때, $\displaystyle \lim_{x \to \infty}\frac{2x^{2}-1}{\{f(x)\}^{2}+3x^2}$의 값은? [3점]
① $\frac{1}{6}$
② $\frac{1}{3}$
③ $\frac{1}{2}$
④ $\frac{2}{3}$
⑤ $\frac{5}{6}$
7. 두 함수 $y = f(x)$, $y = g(x)$의 그래프가 그림과 같다.
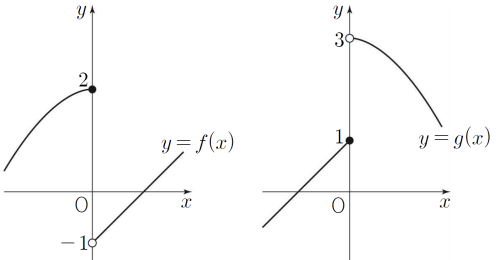
$\displaystyle \lim_{x \to 0}\{ f(x)+kg(x) \}$의 값이 존재할 때, 상수 $k$의 값은? [3점]
① $\frac{1}{2}$
② $1$
③ $\frac{3}{2}$
④ $2$
⑤ $\frac{5}{2}$
8. 함수 $f(x) = \log_{a}(3x+1)+2$가 닫힌구간 $[\,0, \,5\,]$에서 최솟값 $\dfrac{2}{3}$를 가질 때, $a$의 값은? (단, $a$는 $1$이 아닌 양의 상수이다.) [3점]
① $\frac{1}{32}$
② $\frac{1}{8}$
③ $\frac{1}{2}$
④ $2$
⑤ $8$
9. 실수 전체의 집합에서 연속인 함수 $f(x)$가 모든 실수 $x$에 대하여 $$(x-1)f(x) = \sqrt{x^{2}+3}+a$$ 를 만족시킬 때, $f(1)$의 값은? (단, $a$는 상수이다.) [3점]
① $\frac{1}{4}$
② $\frac{1}{2}$
③ $\frac{3}{4}$
④ $1$
⑤ $\frac{5}{4}$
②
$(x-1)f(x) = \sqrt{x^{2}+3}+a$의 양변에 $x=1$을 대입하면
$0 = \sqrt{1^{2}+3}+a$에서 $a = -1$
$x \ne 1$일 때, $f(x) = \frac{\sqrt{x^{2}+3}-2}{x-1}$
함수 $f(x)$는 $x=1$에서 연속이므로
$\begin{align}f(1) &= \displaystyle \lim_{x \to 1}f(x) \\
&= \lim_{x \to 1}\frac{\sqrt{x^{2}+3}-2}{x-1} \\
&= \lim_{x \to 1}\frac{x^{2}-1}{(x-1)(\sqrt{x^{2}+3}+2)} \\
&= \lim_{x \to 1}\frac{x+1}{\sqrt{x^{2}+3}+2} = \frac{1+1}{\sqrt{1^{2}+3}+2} = \frac{1}{2}\end{align}$
10. 최고차항의 계수가 $1$인 이차함수 $f(x)$에서 $x$의 값이 $0$에서 $6$까지 변할 때의 평균변화율이 $0$일 때, $f'(4)$의 값은? [3점]
① $2$
② $4$
③ $6$
④ $8$
⑤ $10$
11. 다항함수 $f(x)$에 대하여 $\displaystyle \lim_{h \to 0}\frac{f(1+h)-f(1-h)}{h} = 6$일 때, $\displaystyle \lim_{x \to 1}\frac{f(x^{3})-f(1)}{x-1}$의 값은? [3점]
① $9$
② $11$
③ $13$
④ $15$
⑤ $17$
①
다항함수 $f(x)$는 $x=1$에서 미분가능하므로
$\begin{align} 6 &= \displaystyle \lim_{h \to 0}\frac{f(1+h)-f(1-h)}{h} \\
&= \lim_{h \to 0}\bigg\{ \frac{f(1+h)-f(1)}{h}+\frac{f(1-h)-f(1)}{-h} \bigg\} = 2f'(1) \end{align}$
에서 $f'(1) = 3$
$\begin{align} \lim_{x \to 1}\frac{f(x^{3})-f(1)}{x-1} &= \lim_{x \to 1}\bigg\{ \frac{f(x^{3})-f(1)}{x^{3}-1} \times (x^{2}-x+1) \bigg\} \\
&= f'(1) \times 3 = 9 \end{align}$
12. 수열 $\{ a_n \}$에 대하여 $a_{1} = 1$, $a_{10} = 4$이고 $\displaystyle \sum_{k=1}^{9}(a_{k}+a_{k+1}) = 25$일 때, $\displaystyle \sum_{k=1}^{10}a_{k}$의 값은? [3점]
① $11$
② $12$
③ $13$
④ $14$
⑤ $15$
13. 좌표평면 위에 두 점 $\mathrm{P}(a, b)$, $\mathrm{Q}(a^{2}, -2b^{2})$ ($a \gt 0$, $b \gt 0$)이 있다. 두 동경 $\mathrm{OP}$, $\mathrm{OQ}$가 나타내는 각의 크기를 각각 $\theta_{1}$, $\theta_{2}$라 하자. $\tan \theta_{1}+\tan \theta_{2} = 0$일 때, $\sin \theta_1$의 값은? (단, $\mathrm{O}$는 원점이고, 축의 양의 방향을 시초선으로 한다.) [3점]
① $\frac{2}{5}$
② $\frac{\sqrt{5}}{5}$
③ $\frac{\sqrt{6}}{5}$
④ $\frac{\sqrt{7}}{5}$
⑤ $\frac{2\sqrt{2}}{5}$
②
$a \gt 0$이므로 $\tan \theta_{1} = \frac{b}{a}$, $\tan \theta_{2} = -\frac{2b^{2}}{a^{2}}$
$\tan \theta_{1}+\tan \theta_{2} = \frac{b}{a}+(-\frac{2b^{2}}{a^{2}}) = -\frac{b(a-2b)}{a^{2}} = 0$에서
$b \gt 0$이므로 $a = 2b$
따라서 $\sin \theta_{1} = \frac{b}{\sqrt{a^{2}+b^{2}}} = \frac{b}{\sqrt{5b^{2}}}$ $= \dfrac{\sqrt{5}}{5}$
14. 첫째항이 $1$인 수열 $\{ a_n \}$이 모든 자연수 $n$에 대하여 $$a_{n+1} = \begin{cases} a_{n}-4 & (a_{n} \ge 0) \\ a_{n}^{\,2} & (a_{n} \lt 0) \end{cases}$$ 일 때, $\displaystyle \sum_{k=1}^{22}a_{k}$의 값은? [4점]
① $50$
② $54$
③ $58$
④ $62$
⑤ $66$
③
$a_{1} = 1$이므로
$a_{2} = a_{1}-4 = -3$
$a_{3} = a_{2}^{2} = 9$
$a_{4} = a_{3}-4 = 5$
$a_{5} = a_{4}-4 = 1 = a_{1}$
$a_{6} = a_{5}-4 = -3 = a_2$
$\vdots$
그러므로 수열 $\{ a_n \}$은 모든 자연수 $n$에 대하여 $a_{n+4} = a_n$을 만족시킨다.
$\begin{align} \displaystyle \sum_{k=1}^{22}a_{k} &= \sum_{k=1}^{20}a_{k}+a_{21}+a_{22} \\ &= 5\sum_{k=1}^{4}a_{k}+a_{1}+a_{2} \\ &= 5 \times \{ 1+(-3)+9+5 \}+1+(-3) = 58 \end{align}$
15. 모든 항이 실수인 등비수열 $\{ a_n \}$에 대하여 $$\sum_{k=1}^{20}a_{k}+\sum_{k=1}^{10}a_{2k} = 0$$ 이 성립한다. $a_{3}+a_{4} = 3$일 때, $a_1$의 값은? [4점]
① $12$
② $16$
③ $20$
④ $24$
⑤ $28$
④
등비수열 \{ a_n \}의 공비를 $r$라 하자.
$a_{1}+a_{3}+a_{5}+ \cdots +a_{19} = a_{1}(1+r^{2}+r^{4}+ \cdots +r^{18}) = \alpha$라 하면
$a_{2}+a_{4}+a_{6}+ \cdots +a_{20} = \alpha r$
$\displaystyle \sum_{k=1}^{20}a_{k}+\sum_{k=1}^{10}a_{2k} = 0$이므로
$(\alpha + \alpha r)+ \alpha r = 0$, $(1+2r)\alpha = 0$
$\alpha = 0$이라 하면 $a_{1} = 0$이므로 $a_{3}+a_{4} = 0$
$a_{3}+a_{4} = 3$이므로 $\alpha \ne 0$
그러므로 $r = -\frac{1}{2}$
$a_{3}+a_{4} = a_{1}\times (-\frac{1}{2})^{2}+a_{1}\times (-\frac{1}{2})^{3} = \frac{1}{8}a_{1} = 3$
따라서 $a_{1} = 24$
16. $3 \sin^{2}(\theta+\frac{2}{3}\pi) = 8 \sin (\theta+\frac{\pi}{6})$일 때, $\cos (\theta-\frac{\pi}{3})$의 값은? [4점]
① $\frac{1}{6}$
② $\frac{1}{5}$
③ $\frac{1}{4}$
④ $\frac{1}{3}$
⑤ $\frac{1}{2}$
④
$\theta-\frac{\pi}{3} = \alpha$라 하면
$\begin{align} 3 \sin^{2}(\theta+\frac{2}{3}\pi) &= 3 \sin^{2}(\pi + \alpha) \\ &= 3 \sin^{2}\alpha = 3-3\cos^{2}\alpha \end{align}$
이고
$8 \sin (\theta+\frac{\pi}{6}) = 8 \sin (\frac{\pi}{2}+\alpha) = 8\cos \alpha$
$3-3\cos^{2}\alpha = 8\cos \alpha$에서
$3\cos^{2}\alpha+8\cos \alpha-3 = 0$
$(3\cos\alpha-1)(\cos \alpha+3) = 0$
$-1 \le \cos \alpha \le 1$이므로 $\cos \alpha = \frac{1}{3}$
따라서 $\cos (\theta-\frac{\pi}{3}) = \cos \alpha = \dfrac{1}{3}$
17. 다항함수 $f(x)$에 대하여 함수 $g(x)$를 $$g(x) = (x^{2}-2x+2)f(x)$$ 라 하자. $\displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1} = -2$일 때, $g'(2)$의 값은? [4점]
① $\frac{1}{3}$
② $\frac{2}{3}$
③ $1$
④ $\frac{4}{3}$
⑤ $\frac{5}{3}$
②
$g(x) = (x^{2}-2x+2)f(x)$에서 $g(2) = 2f(2)$
$g'(x) = (2x-2)f(x)+(x^{2}-2x+2)f'(x)$에서 $g'(2) = 2f(2)+2f'(2)$
$\displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1} = -2$에서
$f(2) \ne \frac{1}{2}$이라 하면
$\displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1} = \frac{g(2)-1}{2f(2)-1} = \frac{2f(2)-1}{2f(2)-1} = 1 \ne -2$
이므로 $f(2) = \frac{1}{2}$
그러므로 $g(2) = 2f(2) = 1$이고 $g'(2) = 2f'(2)+1$
$\begin{align} \displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1} &= \lim_{x \to 2}\frac{g(x)-g(2)}{2 \{ f(x)-f(2) \}} \\ &= \lim_{x \to 2}\frac{\frac{g(x)-g(2)}{x-2}}{2\times \frac{f(x)-f(2)}{x-2}} \end{align}$
이때 $f'(2) = 0$이라 하면 $g'(2) = 1$이므로 $\displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1}$의 값이 존재하지 않는다.
그러므로 $f'(2) \ne 0$
$\begin{align} \displaystyle \lim_{x \to 2}\frac{g(x)-1}{2f(x)-1} &= \frac{g'(2)}{2f'(2)} \\ &= \frac{g'(2)}{g'(2)-1} = -2 \end{align}$
따라서 $g'(2) = \dfrac{2}{3}$
18. $1$이 아닌 양의 실수 전체의 집합에서 정의된 함수 $f(x)$를 $f(x) = 2^{\frac{1}{\log_{2}x}}$이라 하자.
다음은 방정식 $8\times f(f(x)) = f(x^2)$의 모든 해의 곱을 구하는 과정이다.
$x \ne 1$인 모든 양의 실수 $x$에 대하여
$f(f(x)) = 2^{\frac{1}{\log_{2}f(x)}}$에서
$8\times f(f(x)) = 2^{(\fbox{ $\textbf{(가)}$ }+\frac{1}{\log_{2}f(x)})}$이고,
$f(x) = 2^{\frac{1}{\log_{2}x}}$에서 $\log_{2}f(x) = \frac{1}{\fbox{ $\textbf{(나)}$ }}$이다.
방정식 $8\times f(f(x)) = f(x^2)$에서
$2^{(\fbox{ $\textbf{(가)}$ }+\fbox{ $\textbf{(나)}$ })} = 2^{\frac{1}{2\log_{2}x}}$
$\fbox{ $\textbf{(가)}$ }+\fbox{ $\textbf{(나)}$ } = \dfrac{1}{2\log_{2}x}$
그러므로 방정식 $8\times f(f(x)) = f(x^2)$의 모든 해는 방정식 $(\fbox{ $\textbf{(가)}$ }+\fbox{ $\textbf{(나)}$ })\times 2\log_{2}x = 1$의 모든 해와 같다.
따라서 방정식 $8\times f(f(x)) = f(x^2)$의 모든 해의 곱은 $\fbox{ $\textbf{(다)}$ }$이다.
위의 (가), (다)에 알맞은 수를 각각 $p$, $q$라 하고, (나)에 알맞은 식을 $g(x)$라 할 때, $p\times q\times g(4)$의 값은? [4점]
① $\frac{1}{4}$
② $\frac{3}{8}$
③ $\frac{1}{2}$
④ $\frac{5}{8}$
⑤ $\frac{3}{4}$
⑤
$x \ne 1$인 모든 양의 실수 $x$에 대하여
$f(f(x)) = 2^{\frac{1}{\log_{2}f(x)}}$에서
$8 \times f(f(x)) = 2^{(\fbox{ $3$ }+\frac{1}{\log_{2}f(x)})}$이고,
$f(x) = 2^{\frac{1}{\log_{2}x}}$에서 $\log_{2}f(x) = \frac{1}{\fbox{ $\log_{2}x$ }}$이다.
$f(x^2) = 2^{\frac{1}{\log_{2}x^{2}}} = 2^{\frac{1}{2\log_{2}x}}$이므로
방정식 $8\times f(f(x)) = f(x^2)$에서
$2^{(\fbox{ $3$ }+\fbox{ $\log_{2}x$ })} = 2^{\frac{1}{2\log_{2}x}}$
$\fbox{ $3$ }+\fbox{ $\log_{2}x$ } = \frac{1}{2\log_{2}x}$
그러므로 방정식 $8\times f(f(x)) = f(x^2)$의 모든 해는
방정식 $(\fbox{ $3$ }+\fbox{ $\log_{2}x$ })\times 2\log_{2}x = 1$의 모든 해와 같다.
$2(\log_{2}x)^{2}+6\log_{2}x-1 = 0$에서 $\log_{2}x = t$라 하자.
이차방정식 $2t^{2}+6t-1 = 0$의 판별식을 $D$라 하면
$\frac{D}{4} = 3^{2}-2\times (-1) = 11 \gt 0$이므로
이차방정식 $2t^{2}+6t-1 = 0$은 서로 다른 두 실근을 갖는다. 이차방정식 $2t^{2}+6t-1 = 0$의 두 실근을 $\alpha$, $\beta$라 하면 방정식 $2(\log_{2}x)^{2}+6\log_{2}x-1 = 0$은
$2^{\alpha}$, $2^{\beta}$을 서로 다른 두 실근으로 갖는다.
이때 이차방정식 $2t^{2}+6t-1 = 0$에서 근과 계수의 관계에 의하여 $\alpha+\beta = -3$
따라서 방정식 $8\times f(f(x)) = f(x^2)$의 모든 해의 곱은
$2^{\alpha}\times 2^{\beta} = 2^{\alpha+\beta} = 2^{-3} = \fbox{ $\frac{1}{8}$ }$이다.
따라서 $p = 3$, $q = \frac{1}{8}$, $g(x) = \log_{2}x$이므로
$p \times q \times g(4) = 3 \times \frac{1}{8} \times \log_{2}4 = \dfrac{3}{4}$
19. 두 집합
$$\begin{align} A &= \{ \,(x, y)\, |\, x^{2}+y^{2}=5,\, y \ge 0 \, \}, \\ B &= \{\, (x, y)\, |\, y = 2|x|\, \} \end{align}$$
에 대하여 좌표평면에서 집합 $A \cup B$가 나타내는 도형을 $S$라 하자. 양의 실수 $m$에 대하여 직선 $y = m(x+5)$가 도형 $S$와 만나는 점의 개수를 $f(m)$이라 할 때, 열린구간 $(0, \infty)$에서 함수 $f(m)$은 $m = \alpha_{1}$, $m = \alpha_{2}$, $m = \alpha_{3}$에서만 불연속이다.
$\alpha_{1}+\alpha_{2}+\alpha_{3}$의 값은? [4점]
① $\frac{17}{6}$
② $3$
③ $\frac{19}{6}$
④ $\frac{10}{3}$
⑤ $\frac{7}{2}$
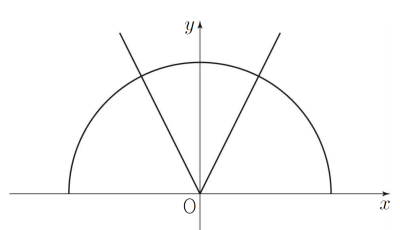
①
직선 $y = m(x+5)$는 기울기가 $m$이고 점 $(-5, 0)$을 지나는 직선이다.
함수 $y = 2|x|$의 그래프와 곡선 $x^{2}+y^{2}= 5$ ($y \ge 0$)은 두 점 $(-1, 2)$, $(1, 2)$에서 만난다.
직선 $y = m(x+5)$가 점 $(1, 2)$를 지날 때 $m = \frac{1}{3}$
직선 $y = m(x+5)$가 점 $(-1, 2)$를 지날 때 $m = \frac{1}{2}$
이때 두 점 $(0, 0)$, $(-1, 2)$를 지나는 직선의 기울기가 $-2$이므로
곡선 $x^{2}+y^{2}= 5$ ($y \ge 0$) 위의 점 $(-1, 2)$에서의 접선의 기울기는 $\frac{1}{2}$이다.
그러므로 직선 $y = \frac{1}{2}(x+5)$는 곡선 $x^{2}+y^{2}= 5$ ($y \ge 0$) 위의 점 $(-1, 2)$에서의 접선이다.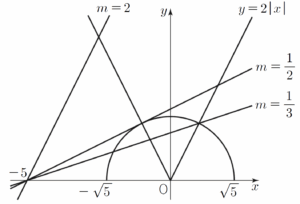
(ⅰ) $0 \lt m \lt \frac{1}{3}$일 때, $f(m) = 4$
(ⅱ) $m = \frac{1}{3}$일 때, $f(m) = 3$
(ⅲ) $\frac{1}{3} \lt m \lt \frac{1}{2}$일 때, $f(m) = 4$
(ⅳ) $\frac{1}{2} \le m \lt 2$일 때, $f(m) = 2$
(ⅴ) $m \ge 2$일 때, $f(m) = 2$
(ⅰ) ~ (ⅴ)에 의하여
$f)m) = \begin{cases} 1 & (m \ge 2) \\ 2 & (\frac{1}{2} \le m \lt 2) \\ 3 & (m = \frac{1}{3}) \\ 4 & (0 \lt m \lt \frac{1}{3} \text{ 또는 } \frac{1}{3} \lt m \lt \frac{1}{2}) \end{cases}$
따라서 열린구간 $(0, \infty)$에서 함수 $f(m)$은 $m = \frac{1}{3}$, $m = \frac{1}{2}$, $m = 2$에서만 불연속이므로
$\alpha_{1}+\alpha_{2}+\alpha_{3} = \frac{1}{3}+\frac{1}{2}+2 = \dfrac{17}{6}$
20. 반지름의 길이가 $\sqrt{3}$인 원 $C$에 내접하는 삼각형 $\mathrm{ABC}$에 대하여 $\angle \mathrm{BAC}$의 이등분선이 원 $C$와 만나는 점 중 $\mathrm{A}$가 아닌 점을 $\mathrm{D}$라 하고, 두 선분 $\mathrm{dBC}$, $\mathrm{AD}$의 교점을 $\mathrm{E}$라 하자.
$\overline{\mathrm{BD}} = \sqrt{3}$일 때, &tl;보기>에서 옳은 것만을 있는 대로 고른 것은? [4점]
ㄱ. $\sin (\angle \mathrm{DBE}) = \dfrac{1}{2}$
ㄴ. $\overline{\mathrm{AB}}^{\,2}+\overline{\mathrm{AC}}^{\,2} = \overline{\mathrm{AB}}\times \overline{\mathrm{AC}}+9$
ㄷ. 삼각형 $\mathrm{ABC}$의 넓이가 삼각형 $\mathrm{BDE}$의 넓이의 $4$배가
되도록 하는 모든 $\overline{\mathrm{BE}}$의 값의 합은 $\dfrac{9}{4}$이다.
① ㄱ
② ㄷ
③ ㄱ, ㄴ
④ ㄴ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
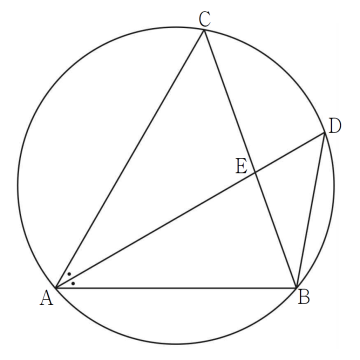
⑤
$\angle \mathrm{DAC} = \angle \mathrm{BAD} = \theta$라 하면 두 각 $\angle \mathrm{DAC}$, $\angle \mathrm{DBC}$가 모두 호 $\mathrm{CD}$에 대한 원주각이므로 $\mathrm{DBC} = \theta$
ㄱ.
삼각형 $\mathrm{ABD}$에서 사인법칙에 의하여
$\frac{\overline{\mathrm{BD}}}{\sin (\angle \mathrm{BAD})} = 2\sqrt{3}$, $\sin \theta = \frac{1}{2}$
$\sin (\angle \mathrm{DBE}) = \sin (\angle \mathrm{DBC}) = \dfrac{1}{2}$ (참)
ㄴ.
$0 \lt \angle \mathrm{BAC}) = 2\theta \lt \pi$에서 $0 \lt \theta \lt \frac{\pi}{2}$이고
$\sin \theta = \frac{1}{2}$이므로 $\theta = \frac{\pi}{6}$
$\angle \mathrm{BAC}) = 2\times \frac{\pi}{6} = \frac{\pi}{3}$
삼각형 $\mathrm{ABC}$에서 사인법칙에 의하여
$\frac{\overline{\mathrm{BC}}}{\sin \frac{\pi}{3}} = 2\sqrt{3}$, $\overline{\mathrm{BC}} = 3$
삼각형 $\mathrm{ABC}$에서 코사인법칙에 의하여
$\overline{\mathrm{BC}}^{2} = \overline{\mathrm{AB}}^{2}+\overline{\mathrm{AC}}^{2}-2\times \overline{\mathrm{AB}}\times \overline{\mathrm{AC}}\times \cos \frac{\pi}{3}$
$\overline{\mathrm{AB}}^{2}+\overline{\mathrm{AC}}^{2} = \overline{\mathrm{AB}}\times \overline{\mathrm{AC}}+9$ $\cdots$ (*) (참)
ㄷ.
$\overline{\mathrm{BE}} = a$ ($0 \lt a \lt 3$)이라 하면
$\overline{\mathrm{CE}} = \overline{\mathrm{BC}}-\overline{\mathrm{BE}} = 3-a$
삼각형 $\mathrm{ABC}$에서 $\angle \mathrm{BAE} = \angle \mathrm{EAC}$이므로
$\overline{\mathrm{AB}} : \overline{\mathrm{AC}} = \overline{\mathrm{BE}} : \overline{\mathrm{CE}}$에서
$\overline{\mathrm{AB}} : \overline{\mathrm{AC}} = a : (3-a)$
양수 $k$에 대하여
$\overline{\mathrm{AB}} = ak$, $\overline{\mathrm{AC}} = (3-a)k$라 하면
삼각형 $\mathrm{ABC}$의 넓이는
$\frac{1}{2}\times \overline{\mathrm{AB}}\times \overline{\mathrm{AC}} \times \sin \frac{\pi}{3} = \frac{\sqrt{3}}{4}a(3-a)k^2$이고
삼각형 $\mathrm{BDE}$의 넓이는
$\frac{1}{2}\times \overline{\mathrm{BD}}\times \overline{\mathrm{BE}} \times \sin \frac{\pi}{6} = \frac{\sqrt{3}}{4}a$
삼각형 $\mathrm{ABC}$의 넓이가 삼각형 $\mathrm{BDE}$의 넓이의 $4$배이어야 하므로
$\frac{\sqrt{3}}{4}a(3-a)k^{2} = 4\times \frac{\sqrt{3}}{4}a$
$(3-a)k^{2} = 4$ $\cdots$ (**)
(*)에 의하여
$(ak)^{2}+\{ (3-a)k\}^{2} = (ak)(3-a)k+9$
$k^{2}(a^{2}-3a+3) = 3$
$(3-a)k^{2}(a^{2}-3a+3) = 3(3-a)$
위 식에 (**)를 대입하면
$4(a^{2}-3a+3) = 3(3-a)$
$4a^{2}-9a+3 = 0$에서
$a = \frac{9+\sqrt{33}}{8}$ 또는 $a = \frac{9-\sqrt{33}}{8}$
그러므로 모든 $a$의 값의 합은 $\dfrac{9}{4}$ (참)
따라서 옳은 것은 ㄱ, ㄴ, ㄷ
21. 공차가 음수인 등차수열 $\{ a_n \}$이 다음 조건을 만족시킬 때, 모든 $a_1$의 값의 합은? [4점]
$|a_{m}| = 2|a_{m+2}|$이면서
$S_{m}$, $S_{m+1}$, $S_{m+2}$ 중에서 가장 큰 값이 $460$이고 가장 작은 값이 $450$이 되도록 하는 자연수 $m$이 존재한다.
(단, $S_n$은 수열 $\{ a_n \}$의 첫째항부터 제$n$항까지의 합이다.)
① $144$
② $148$
③ $152$
④ $156$
⑤ $160$
③
등차수열 $\{ a_n \}$의 공차를 $d$이라 하자.
(ⅰ) $a_{m} = 2a_{m+2}$일 때
$a_{m+2} = a_{m}+2d$이므로
$a_{m} = -4d$이고 $a_{m+1} = -3d$, $a_{m+2} = -2d$
$S_{m+1} = S_{m}+(-3d) \gt S_{m}$,
$S_{m+2} = S_{m+1}+(-2d) \gt S_{m+1}$이므로
$S_{m+2} \gt S_{m+1} \gt S_{m}$
그러므로 $S_{m+2} = 460$, $S_{m} = 450$
$S_{m+2}-S_{m} = a_{m+1}+a_{m+2}$에서
$460-450 = -3d+(-2d)$
$d = -2$
$a_{m} =8 = a_{1}+(m-1)\times (-2)$에서 $a_{1} = 2m+6$
$\begin{align} S_{m} &= \frac{m(a_{1}+a_{m})}{2} \\ &= \frac{m(2m+14)}{2} = 450 \end{align}$
$m^{2}+7m-450 = 0$, $(m+25)(m-18) = 0$
$m$은 자연수이므로 $m = 18$
그러므로 $a_{1} = 2\times 18+6 =42$
(ⅱ) $a_{m} = -2a_{m+2}$일 때
$a_{m+2} = a_{m}+2d$이므로
$a_{m} = -\frac{4}{3}d$이고 $a_{m+1} = -\frac{d}{3}$, $a_{m+2} = \frac{2}{3}d$
$S_{m+1} = S_{m}+(-\frac{d}{3}) \gt S_{m}$,
$S_{m+2} = S_{m}+\frac{d}{3} \lt S_{m}$이므로
$S_{m+1} \gt S_{m} \gt S_{m+2}$
그러므로 $S_{m+1} = 460$, $S_{m+2} = 450$
$S_{m+2}-S_{m+1} = a_{m+2}$에서 $450-460 = \frac{2}{3}d$
$d = -15$
$a_{m+1} = 5 = a_{1} + m\times (-15)$에서 $a_{1} = 15m+5$
$\begin{align} S_{m+1} &= \frac{(m+1)(a_{1}+a_{m+1})}{2} \\ &= \frac{(m+1)(15m+10)}{2} = 460 \end{align}$
$3m^{2}+5m-182 = 0$, $(3m+26)(m-7) = 0$
$m$은 자연수이므로 $m=7$
그러므로 $a_{1} = 15\times 7+5 = 110$
(ⅰ), (ⅱ)에 의하여 모든 $a_{1}$의 값의 합은
$42+110 = 152$
24. 함수 $y = 2^{x}$의 그래프를 $x$축의 방향으로 $a$만큼, $y$축의 방향으로 $3$만큼 평행이동한 그래프가 함수 $y = \log_{2}(4x-b)$의 그래프와 직선 $y = x$에 대하여 대칭일 때, $a+b$의 값을 구하시오. (단, $a$와 $b$는 상수이다.) [3점]
$14$
곡선 $y = 2^{x}$을 $x$축의 방향으로 $a$만큼, $y$축의 방향으로 $3$만큼 평행이동하면 곡선 $y = 2^{x-a}+3$이다.
또한 곡선 $y = 2^{x-a}+3$을 직선 $y = x$에 대하여 대칭이동하면 곡선 $y = \log_{2}(x-3)+a$이다.
$\log_{2}(x-3)+a = \log_{2}(2^{a}x-3\times 2^{a})$이고,
함수 $y = \log_{2}(2^{a}x-3\times 2^{a})$의 그래프가 함수 $y = \log_{2}(4x-b)$의 그래프와 일치하므로
$2^{a} = 4$에서 $a = 2$이고 $b = 3 \times 2^{a} = 12$
따라서 $a+b = 2+12 = 14$
25. 선분 $\mathrm{AB}$를 지름으로 하는 반원의 호 $\mathrm{AB}$ 위에 점 $\mathrm{C}$가 있다. 선분 $\mathrm{AB}$의 중점을 $\mathrm{O}$라 할 때, 호 $\mathrm{AC}$의 길이가 $\pi$이고 부채꼴 $\mathrm{OBC}$의 넓이가 $15\pi$이다. 선분 $\mathrm{OA}$의 길이를 구하시오. (단, 점 $\mathrm{C}$는 점 $\mathrm{A}$도 아니고 점 $\mathrm{B}$도 아니다.) [3점]
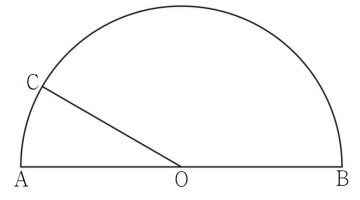
$6$
$\overline{\mathrm{OA}} = r$ ($r \gt 0$), $\angle \mathrm{COA} = \theta$ ($0 \lt \theta \lt \pi$)라 하면
호 $\mathrm{AC}$의 길이가 $\pi$이므로 $r\theta = \pi$에서 $\theta = \frac{\pi}{r}$
부채꼴 $\mathrm{OBC}$의 넓이가 $15\pi$이므로
$\begin{align}15\pi &= \frac{1}{2}r^{2}(\pi-\frac{\pi}{r}) \\ &= \frac{1}{2}r^{2}(\pi-\theta) \\ &= \frac{1}{2}\pi (r^{2}-r) \end{align}$
$r^{2}-r-30 = 0$, $(r-6)(r+5) = 0$에서 $r = 6$
따라서 선분 $\mathrm{OA}$의 길이는 $6$
26. 수열 $\{ a_n \}$의 첫째항부터 제$n$항까지의 합을 $S_n$이라 하자. 모든 자연수 $n$에 대하여 $S_{n} = \dfrac{n}{2n+1}$일 때, $\displaystyle \sum_{k=1}^{6}\frac{1}{a_k}$의 값을 구하시오. [4점]
$358$
$a_{1} = S_{1} = \frac{1}{3}$
$n \ge 2$일 때 $\begin{align} a_{n} &= S_{n}-S_{n-1} &= \frac{n}{2n+1}-\frac{n-1}{2n-1} \\ &= \frac{1}{4n^{2}-1} \end{align}$
그러므로 모든 자연수 $n$에 대하여 $a_{n} = \frac{1}{4n^{2}-1}$
따라서 $\begin{align} \displaystyle \sum_{k=1}^{6}\frac{1}{a_k} &= \sum_{k=1}^{6}(4k^{2}-1) \\ &= 4\sum_{k=1}^{6}k^{2}-\sum_{k=1}^{6}1 \\ &= 4\times \frac{6\times 7\times 13}{6}-6 = 358 \end{align}$
27. 일차함수 $f(x)$와 최고차항의 계수가 $1$인 이차함수 $g(x)$에 대하여 $$\lim_{x \to -3}\frac{f(x)g(x)}{(x+3)^{2}}=4, \:\lim_{x \to -3}\frac{f(x)+g(x)}{x+3}=-4$$ 일 때, $g(2)-f(2)$의 값을 구하시오. [4점]
$25$
두 함수 $f(x)g(x)$, $f(x)-g(x)$는 $x = -3$에서 연속이다.
$\displaystyle \lim_{x \to -3}\frac{f(x)g(x)}{(x+3)^{2}}=4$에서 $\displaystyle \lim_{x \to -3}(x+3)^{2} = 0$이므로
$\displaystyle \lim_{x \to -3}f(x)g(x) = f(-3)g(-3) = 0$ $\cdots$ ㉠
$\displaystyle \lim_{x \to -3}\frac{f(x)+g(x)}{x+3}=-4$에서 $\displaystyle \lim_{x \to -3}(x+3) = 0$이므로
$\displaystyle \lim_{x \to -3}\{ f(x)+g(x) \} = f(-3)+g(-3) = 0$ $\cdots$ ㉡
㉠, ㉡에 의하여 $f(-3) = g(-3) = 0$이므로
두 함수 $f(x)$, $g(x)$는 각각 $x+3$을 인수로 갖는다.
$f(x) = a(x+3)$, $g(x) = (x+3)(x+b)$ ($a$, $b$는 상수)라 하면
$\begin{align} \displaystyle \lim_{x \to -3}\frac{f(x)g(x)}{(x+3)^{2}} &= \lim_{x \to -3}\frac{a(x+3)^{2}(x+b)}{(x+3)^{2}} \\ &= \lim_{x \to -3}a(x+b) \\ &= a(-3+b) = 4 \: \cdots \text{ ㉢} \end{align}$
$\begin{align} \displaystyle \lim_{x \to -3}\frac{f(x)+g(x)}{x+3} &= \lim_{x \to -3}\frac{a(x+3)+(x+3)(x+b)}{x+3} \\ &= \lim_{x \to -3}(a+x+b) \\ &= a-3+b = -4 \: \cdots \text{ ㉣} \end{align}$
㉢, ㉣을 연립하면
$a(-a-4) = 4$, $a^{2}+4a+4 = 0$
$(a+2)^{2} = 0$에서 $a = -2$이고 $b=1$
$f(x) = -2(x+3)$, $g(x) = (x+3)(x+1)$
따라서 $g(2)-f(2) = 5\times 3-(-2)\times 5 = 25$
28. 자연수 $n$에 대하여 닫힌구간 $[\,0, \,n\,]$에서 함수 $y = 2 \sin \{ \frac{\pi}{6}(x+1) \}$의 최댓값을 $f(n)$, 최솟값을 $g(n)$이라 할 때, 부등식 $2 \lt f(n)-g(n) \lt 4$를 만족시키는 모든 $n$의 값의 합을 구하시오. [4점]
$13$
함수 $y = 2 \sin \{ \frac{\pi}{6}(x+1) \}$의 주기는 $\dfrac{2\pi}{|\frac{\pi}{6}|} = 12$이고, 최댓값과 최솟값은 각각 $2$, $-2$이다.
또한 함수 $y = 2 \sin \{ \frac{\pi}{6}(x+1) \}$의 그래프는 함수 $y = 2 \sin \frac{\pi}{6}x$의 그래프를 $x$축의 방향으로 $-1$만큼 평행이동한 그래프이다.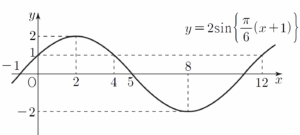 
(ⅰ) $1 \le n \le 5$일 때
$f(1) = \sqrt{3}$, $2 \le n \le 5$일 때 $f(n) = 2$이고
$1 \le n \le 4$일 때 $g(n) = 1$, $g(5) = 0$이므로
$f(1)-g(1) = \sqrt{3}-1$, $f(5)-g(5) = 2$, $2 \le n \le 4$일 때 $f(n)-g(n) = 1$
그러므로 부등식 $2 \lt f(n)-g(n) \lt 4$를 만족시키는 자연수 $n$은 존재하지 않는다.
(ⅱ) $n = 6, 7$일 때
$f(n) = 2$이고 $g(6) = -1$, $g(7) = -\sqrt{3}$이므로
$f(6)-g(6) = 3$, $f(7)-g(7) = 2+\sqrt{3}$
그러므로 부등식 $2 \lt f(n)-g(n) \lt 4$를 만족시키는 자연수 $n$의 값은 $6$, $7$
(ⅲ) $n \ge 8$일 때
$f(n) = 2$이고 $g(n) = -2$이므로 $f(n)-g(n) = 4$
그러므로 부등식 $2 \lt f(n)-g(n) \lt 4$를 만족시키는 자연수 $n$은 존재하지 않는다.
(ⅰ), (ⅱ), (ⅲ)에 의하여 부등식 $2 \lt f(n)-g(n) \lt 4$를 만족시키는 모든 자연수 $n$의
값의 합은 $6+7 = 13$
29. 두 자연수 $a$, $b$에 대하여 두 함수 $f(x)$, $g(x)$를 $$\begin{align} f(x) &= \begin{cases} x+5 & (x \lt 5) \\ |\,2x-a\,| & (x \ge 5) \end{cases}, \\ g(x) &= (x-5)(x-b) \end{align}$$ 라 하자. 함수 $f(x)g(x)$가 실수 전체의 집합에서 미분가능하도록 하는 $a$, $b$의 모든 순서쌍 $(a, b)$의 개수를 구하시오. [4점]
$11$
함수 $g(x)$는 실수 전체의 집합에서 미분가능하다.
(ⅰ) $a \le 10$일 때
$f(x) = \begin{cases} x+5 & (x \lt 5) \\ 2x-a & (x \ge 5) \end{cases}$이므로 함수 $f(x)g(x)$가 실수 전체의 집합에서 미분가능하기 위해서는 $x=5$에서 미분가능하여야 한다.
$\displaystyle \lim_{x \to 5-}\frac{f(x)g(x)-f(5)g(5)}{x-5}$
$=\displaystyle \lim_{x \to 5-}\frac{(x+5)(x-5)(x-b)}{x-5}$
$=\displaystyle \lim_{x \to 5-}(x+5)(x-b) = 10(5-b)$
$\displaystyle \lim_{x \to 5=}\frac{f(x)g(x)-f(5)g(5)}{x-5}$
$=\displaystyle \lim_{x \to 5+}\frac{(2x-a)(x-5)(x-b)}{x-5}$
$=\displaystyle \lim_{x \to 5+}(2x-a)(x-b) = (10-a)(5-b)$
에서 $10(5-b) = (10-a)(5-b)$, $a(5-b) = 0$
$a$는 자연수이므로 $b=5$
그러므로 순서쌍 $(a, b)$는
$(1, 5)$, $(2, 5)$, $(3, 5)$, $\cdots$, $(10, 5)$
(ⅱ) $a \ge 11$일 때
$f(x) = \begin{cases} x+5 & (x \lt 5) \\ -2x+a & (5 \le x \lt \frac{a}{2}) \\ 2x-a & (x \ge \frac{a}{2}) \end{cases}$이므로 함수 $f(x)g(x)$가 실수 전체의 집합에서 미분가능하기 위해서는 $x = 5$와 $x = \frac{a}{2}$에서 미분가능하여야 한다.
$\displaystyle \lim_{x \to 5-}\frac{f(x)g(x)-f(5)g(5)}{x-5} = 10(5-b)$
$\displaystyle \lim_{x \to 5=}\frac{f(x)g(x)-f(5)g(5)}{x-5}$
$=\displaystyle \lim_{x \to 5+}\frac{(-2x+a)(x-5)(x-b)}{x-5}$
$=\displaystyle \lim_{x \to 5+}(-2x+a)(x-b) = (-10+a)(5-b)$
에서 $10(5-b) = (-10+a)(5-b)$, $(a-20)(5-b) = 0$
$a = 20$ 또는 $b=5$ $\cdots$ ㉠
또한 $\displaystyle \lim_{x \to \frac{a}{2}-}\frac{f(x)g(x)-f(\frac{a}{2})g(\frac{a}{2})}{x-\frac{a}{2}}$
$=\displaystyle \lim_{x \to \frac{a}{2}-}\frac{(-2x+a)(x-5)(x-b)}{x-\frac{a}{2}}$
$=\displaystyle \lim_{x \to \frac{a}{2}-}\{-2(x-5)(x-b)\} = (-a+10)(\frac{a}{2}-b)$
$\displaystyle \lim_{x \to \frac{a}{2}+}\frac{f(x)g(x)-f(\frac{a}{2})g(\frac{a}{2})}{x-\frac{a}{2}}$
$=\displaystyle \lim_{x \to \frac{a}{2}+}\frac{(2x-a)(x-5)(x-b)}{x-\frac{a}{2}}$
$=\displaystyle \lim_{x \to \frac{a}{2}+}2(x-5)(x-b) = (a-10)(\frac{a}{2}-b)$
에서 $(-a+10)(\frac{a}{2}-b) = (a-10)(\frac{a}{2}-b)$
$(a-10)(a-2b) = 0$
$a \ge 11$이므로 $a = 2b$ $\cdots$ ㉡
그러므로 ㉠, ㉡에 의하여 순서쌍 $(a, b)$는
$(20, 10)$
(ⅰ), (ⅱ)에 의하여 모든 순서쌍 $(a, b)$의 개수는 $11$
30. 양의 실수 $a$에 대하여 함수 $f(x)$를 $$f(x) = \begin{cases} 2^{x}+2^{-a}-2 & (x \lt a) \\ 2^{-x}+2^{a}-2 & (x \ge a) \end{cases}$$ 라 할 때, 함수 $f(x)$가 다음 조건을 만족시키도록 하는 $a$의 최댓값을 $M$, 최솟값을 $m$이라 하자.
함수 $y = |f(x)|$의 그래프와 직선 $y = k$가 서로 다른 두 점에서 만나도록 하는 양수 $k$는 오직 하나뿐이다.
$2^{M+m} = p+\sqrt{q}$일 때, $p+q$의 값을 구하시오. (단, $p$와 $q$는 자연수이다.) [4점]
$4$
$f_{1}(x) = 2^{x}+2^{-a}-2$, $f_{2}(x) = 2^{-x}+2^{a}-2$라 하면 함수 $y = f_{1}(x)$의 $x$값이 증가하면 $y$의 값이 증가하고, 함수 $y = f_{2}(x)$는 $x$의 값이 증가하면 $y$의 값은 감소한다.
두 함수 $y = f_{1}(x)$, $y = f_{2}(x)$의 그래프의 점근선은 각각 $y = 2^{-a}-2$, $y = 2^{a}-2$이다.
$\alpha = 2^{-a}-2$, $\beta = 2^{a}-2$라 하면 두 함수 $y = |f_{1}(x)|$, $y = |f_{2}(x)|$의 그래프의 점근선은 각각 $y = |\alpha|$, $y = |\beta|$이다.
$\beta-\alpha = 2^{a}-2^{-a} \gt 0$이므로 $\beta-\alpha$, $-2 \lt \alpha \lt -1$이므로 $\alpha \lt 0$이고 $|\alpha| = -\alpha$
$f(a) = 2^{-a}+2^{a}-2 \gt 2\sqrt{2^{-a}\times 2^{a}}-2 = 0$이므로 $f(a) \gt 0$
(ⅰ) $0 \lt a \lt 1$일 때
$1 \lt 2^{a} \lt 2$, $\frac{1}{2} \lt 2^{-a} \lt 1$이므로 $-\frac{1}{2} \lt f(a) \lt 1$이고 $1 \lt -\alpha \lt \frac{3}{2}$
그러므로 $f(a) \lt -\alpha$
한편 $-1 \lt \beta \lt 0$이므로 $|\beta| = -\beta$
$f(a) = -\beta$에서 $2^{-a}+2^{a}-2 = -2^{a}+2$,
$2\times (2^{a})^{2}-4\times 2^{a}+1 = 0$
$a = \log_{2}\frac{2+\sqrt{2}}{2}$
그러므로 $a = \log_{2}\frac{2+\sqrt{2}}{2}$의 좌우에서 $-\beta$, $f(a)$의 값의 대소 관계가 달라진다.
(a) $0 \lt a \lt \log_{2}\frac{2+\sqrt{2}}{2}$일 때
$f(a) \lt -\beta \lt -\alpha$이므로 그림과 같이 $f(a) \lt k \lt -\beta$인 임의의 양수 $k$에 대하여 함수 $y = |f(x)|$의 그래프와 직선 $y = k$가 서로 다른 두 점에서 만난다.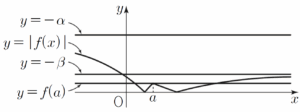 
(b) $\log_{2}\frac{2+\sqrt{2}}{2} \le a \lt 1$일 때
$-\beta \le f(a) \lt -\alpha$이므로 그림과 같이 함수 $y = |f(x)|$의 그래프와 직선 $y = k$가 서로 다른 두 점에서 만나도록 하는 양수 $k$의 값은$k = f(a)$ 뿐이다.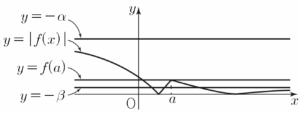 
(ⅱ) $a=1$일 때
$-\alpha = \frac{3}{2}$, $\beta = 0$이고 $f(a) = \frac{1}{2}$이므로 그림과 같이 함수 $y = |f(x)|$의 그래프와 직선 $y = k$가 서로 다른 두 점에서 만나도록 하는 양수 $k$의 값은 $k = \frac{1}{2}$뿐이다.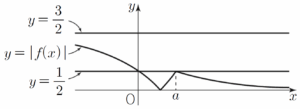 
(ⅲ) $a \gt 1$일 때
$\beta \gt 0$이므로 $|\beta| = \beta$
$f(a) = -\alpha$에서 $2^{-a}+2^{a}-2 = -2^{-a}+2$,
$(2^{a})^{2}-4\times 2^{a}+2 = 0$
$a = \log_{2}(2+\sqrt{2})$
또한 $-\alpha = \beta$에서 $-2^{-a}+2 = 2^{a}-2$,
$(2^{a})^{2}-4\times 2^{a}+1 = 0$
$a = \log_{2}(2+\sqrt{3})$
그러므로 $a = \log_{2}(2+\sqrt{2})$, $a = \log_{2}(2+\sqrt{3})$의 좌우에서 $-\alpha$, $\beta$, $f(a)$의 값의 대소 관계가 달라진다.
(a) $1 \lt a \le \log_{2}(2+\sqrt{2})$일 때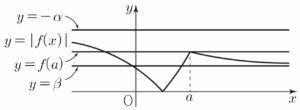 
(b) $\log_{2}(2+\sqrt{2}) \lt a \lt \log_{2}(2+\sqrt{3})$일 때 
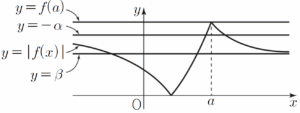(c) $a \ge \log_{2}(2+\sqrt{3})$일 때 
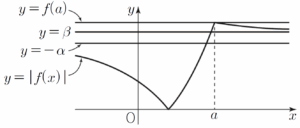(a), (b), (c)에 의하여
$-\alpha$, $\beta$ 중 크지 않은 값을 $s$라 하면 $0 \lt k \lt s$인 임의의 양수 $k$에 대하여 함수 $y = |f(x)|$의 그래프와 직선 $y = k$는 서로 다른 두 점에서 만난다.
(ⅰ), (ⅱ), (ⅲ)에 의하여 함수 $y = |f(x)|$의 그래프와 직선 $y = k$가 서로 다른 두 점에서 만나도록 하는 양수 $k$가 오직 하나뿐인 $a$의 값의 범위는
$\log_{2}\frac{2+\sqrt{2}}{2} \le a \le 1$이므로
$M = 1$, $m = \log_{2}\frac{2+\sqrt{2}}{2}$
$2^{M+m} = 2^{1+\log_{2}\frac{2+\sqrt{2}}{2}} = 2+\sqrt{2}$에서 $p = 2$, $q = 2$
따라서 $p+q = 4$