미분법
람다 $\lambda$의 차례
지수함수와 로그함수의 극한과 미분
1. 지수함수의 극한
지수함수 $y = a^{x}$ ($a \gt 0$, $a \ne 1$)에서
① $a \gt 1$일 때,
$\displaystyle \lim_{x \to r}a^{x} = a^{r}$ ($r$은 실수), $\displaystyle \lim_{x \to \infty}a^{x} = \infty$, $\displaystyle \lim_{x \to -\infty}a^{x} = 0$
② $0 \lt a \lt 1$일 때,
$\displaystyle \lim_{x \to r}a^{x} = a^{r}$ ($r$은 실수), $\displaystyle \lim_{x \to \infty}a^{x} = 0$, $\displaystyle \lim_{x \to -\infty}a^{x} = \infty$
2. 로그함수의 극한
로그함수 $y = \log_{a}x$ ($a \gt 0$, $a \ne 1$)에서
① $a \gt 1$일 때,
$\displaystyle \lim_{x \to r}\log_{a}x = \log_{a}r$ ($r$은 양의 실수), $\displaystyle \lim_{x \to 0+}\log_{a}x = -\infty$, $\displaystyle \lim_{x \to \infty}\log_{a}x = \infty$
② $0 \lt a \lt 1$일 때,
$\displaystyle \lim_{x \to r}\log_{a}x = \log_{a}r$ ($r$은 양의 실수), $\displaystyle \lim_{x \to 0+}\log_{a}x = \infty$, $\displaystyle \lim_{x \to \infty}\log_{a}x = – \infty$
3. 무리수 $e$와 자연로그
(1) 무리수 $e$
$$\lim_{x \to 0}(1 + x)^{\frac{1}{x}} = e\:\,(e = 2.71828182845\cdots)$$
(2) 자연로그
밑이 $e$인 로그 $\log_{e}x$를 $x$의 자연로그라 하고 간단히 $\ln x$로 나타냅니다.
4. 지수함수와 로그함수의 극한
$a \gt 0$, $a \ne 1$일 때
① $\displaystyle \lim_{x \to 0}\dfrac{\ln (1 + x)}{x} = 1$
② $\displaystyle \lim_{x \to 0}\dfrac{e^{x} -\,1}{x} = 1$
③ $\displaystyle \lim_{x \to 0}\dfrac{\log_{a} (1 + x)}{x} = \dfrac{1}{\ln a}$
④ $\displaystyle \lim_{x \to 0}\dfrac{a^{x} -\,1}{x} = \ln a$
5. 지수함수의 도함수
(1) $y = e^{x}$이면 $\dfrac{dy}{dx} = e^{x}$
(2) $y = a^{x}$ ($a \gt 0$, $a \ne 1$)이면 $\dfrac{dy}{dx} = a^{x} \ln a$
6. 로그함수의 도함수
(1) $y = \ln x$이면 $\dfrac{dy}{dx} = \dfrac{1}{x}$
(2) $y = \log_{a}x$ ($a \gt 0$, $a \ne 1$)이면 $\dfrac{dy}{dx} = \dfrac{1}{x \ln a}$
삼각함수의 덧셈정리
1. 삼각함수
(1) $\csc \theta$, $\sec \theta$, $\cot \theta$의 정의
각 $\theta$를 나타내는 동경과 원점 $\mathrm{O}$를 중심으로 하고 반지름의 길이가 $r$인 원의 교점 $\mathrm{P}(x, y)$라 할 때, $$\csc \theta = \dfrac{r}{y}\:(y \ne 0), \,\:\sec \theta = \dfrac{r}{x}\:(x \ne 0), \,\:\cot \theta = \dfrac{x}{y}\:(y \ne 0)$$와 같이 정의된 함수를 차례대로 $\theta$에 대한 코시컨트함수, 시컨트함수, 코탄젠트함수라고 합니다.
(2) 삼각함수 사이의 관계
① $\tan^{2}\theta + 1 = \sec^{2}\theta$
② $1 + \cot^{2}\theta + 1 = \csc^{2}\theta$
2. 삼각함수의 덧셈정리
(1) 삼각함수의 덧셈정리
① $\sin(\alpha + \beta) = \sin \alpha \cos \beta + \cos \alpha \sin \beta$
$\sin(\alpha -\,\beta) = \sin \alpha \cos \beta -\,\cos \alpha \sin \beta$
② $\cos(\alpha + \beta) = \cos \alpha \cos \beta -\,\sin \alpha \sin \beta$
$\cos(\alpha -\,\beta) = \cos \alpha \cos \beta + \sin \alpha \sin \beta$
③ $\tan (\alpha + \beta) = \dfrac{\tan \alpha + \tan \beta}{1 -\,\tan \alpha \tan \beta}$
$\tan (\alpha -\,\beta) = \dfrac{\tan \alpha -\,\tan \beta}{1 + \tan \alpha \tan \beta}$
(2) 배각의 공식
① $\sin 2\alpha = 2\sin \alpha \cos \beta$
② $\cos 2\alpha = \cos^{2} \alpha -\,\sin^{2} \alpha$
③ $\tan 2\alpha = \dfrac{2\tan \alpha}{1 -\,\tan^{2} \alpha}$
3. 삼각함수의 합성
$a \ne 0$, $b \ne 0$일 때
① $a \sin \theta + b \cos \theta = \sqrt{a^{2} + b^2} \sin (\theta + \alpha)$ (단, $\sin \alpha = \frac{b}{\sqrt{a^{2} + b^2}}$, $\cos \alpha = \frac{a}{\sqrt{a^{2} + b^2}}\,$)
② $a \sin \theta + b \cos \theta = \sqrt{a^{2} + b^2} \cos (\theta -\,\alpha)$ (단, $\cos \beta = \frac{b}{\sqrt{a^{2} + b^2}}$, $\sin \beta = \frac{a}{\sqrt{a^{2} + b^2}}\,$)
삼각함수의 극한과 미분
1. 삼각함수의 극한
① $\displaystyle \lim_{x \to 0}\dfrac{\sin x}{x} = 1$
② $\displaystyle \lim_{x \to 0}\dfrac{\tan x}{x} = 1$
③ $\displaystyle \lim_{x \to 0}\dfrac{1 -\,\cos x}{x} = 0$
④ $\displaystyle \lim_{x \to 0}\dfrac{1 -\,\cos x}{x^{2}} = \dfrac{1}{2}$
2. 삼각함수의 미분
① $y = \sin x$이면 $\dfrac{dy}{dx} = \cos x$
② $y = \cos x$이면 $\dfrac{dy}{dx} = – \sin x$
함수의 몫의 미분법으로 부터
③ $y = \tan x$이면 $\dfrac{dy}{dx} = \sec^{2} x$
④ $y = \csc x$이면 $\dfrac{dy}{dx} = -\csc x \cot x$
⑤ $y = \sec x$이면 $\dfrac{dy}{dx} = \sec x \tan x$
⑥ $y = \cot x$이면 $\dfrac{dy}{dx} = -\csc^{2} x$
함수의 몫의 미분법
1. 함수의 몫의 미분법
두 함수 $f(x)$, $g(x)$ ($g(x) \ne 0$)가 미분가능할 때
① $y = \dfrac{1}{g(x)}$이면 $y^{\prime} = – \dfrac{g^{\prime}(x)}{\{g(x)\}^{2}}$
② $y = \dfrac{f(x)}{g(x)}$이면 $y^{\prime} = \dfrac{f^{\prime}(x)g(x) -\,f(x)g^{\prime}(x)}{\{g(x)\}^{2}}$
2. 함수 $y = x^{n}$ ($n$은 정수)의 도함수
(1) $n$이 정수일 때, $y = x^{n}$이면 $y^{\prime} = n x^{n -\,1}$
(2) 위의 미분법을 양의 정수와 음의 정수로 구분해보면, $n$이 자연수일 때
① $y = x^{n}$이면 $y^{\prime} = n x^{n -\,1}$ (다항함수의 미분)
② $y = \dfrac{1}{x^{n}}$이면 $y^{\prime} = – \dfrac{n}{x^{n+1}}$
3. 삼각함수의 도함수
① $y = \tan x = \dfrac{\sin x}{\cos x}$이면 $y^{\prime} = \sec^{2} x$
② $y = \sec x = \dfrac{1}{\cos x}$이면 $y^{\prime} = \sec x \tan x$
③ $y = \csc x = \dfrac{1}{\sin x}$이면 $y^{\prime} = -\csc x \cot x$
④ $y = \cot x = \dfrac{\cos x}{\sin x}$이면 $y^{\prime} = -\csc^{2} x$
합성함수의 미분법
1. 합성함수의 미분법
두 함수 $y = f(u)$, $u = g(x)$가 미분가능할 때, 합성함수 $y = f(g(x))$의 도함수는 $$\frac{dy}{dx} = \frac{dy}{du}\cdot\frac{du}{dx}\textbf{ 또는 }y^{\prime} = f^{\prime}(g(x))g^{\prime}(x)$$
2. 함수 $y = x^{n}$ ($n$은 실수)의 도함수
$n$이 실수일 때, $y = x^{n}$ ($x \gt 0$)이면 $y^{\prime} = n x^{n -\,1}$
3. 로그함수의 도함수
① $y = \ln |\,x\,|$이면 $y^{\prime} = \dfrac{1}{x}$
② $y = \log_{a} |\,x\,|$ ($a \gt 0$, $a \ne 1\,$)이면 $y^{\prime} = \dfrac{1}{x \ln a}$
참고로 $y = |\,x\,|$이면 $y^{\prime} = \dfrac{x}{|\,x\,|}$ (단, $x \ne 0\,$)
매개변수로 나타낸 함수의 미분법
두 함수 $x = f(t)$, $y = g(t)$가 $t$에 대하여 미분가능하고 $f^{\prime}(t) \ne 0$일 때 $$\frac{dy}{dx} = \frac{\dfrac{dy}{dt}}{\dfrac{dx}{dt}} = \frac{g^{\prime}(t)}{f^{\prime}(t)}$$
음함수와 역함수 미분법
1. 음함수의 미분법
$x$의 함수 $y$가 $f(x, y) = 0$ 꼴로 주어졌을 때에는 $y$를 $x$의 함수로 보고 각 항을 $x$에 대하여 미분하여 $\dfrac{dy}{dx}$를 구합니다.
2. 역함수의 미분법
미분가능한 함수 $f(x)$의 역함수 $g(x)$가 존재하고 미분가능할 때
① $g^{\prime}(x) = \dfrac{1}{f^{\prime}(g(x))}$ (단, $f^{\prime}(g(x)) \ne 0\,$)
② $f(a) = b$, 즉 $g(b) = a$이면 $g^{\prime}(b) = \dfrac{1}{f^{\prime}(a)}$ (단, $f^{\prime}(a) \ne 0\,$)
이계도함수
1. 이계도함수
함수 $f(x)$의 도함수 $f^{\prime}(x)$가 미분가능할 때, 함수 $f^{\prime}(x)$의 도함수 $\displaystyle \lim_{h \to 0}\dfrac{f^{\prime}(x + h) -\,f^{\prime}(x)}{h}$를 $f(x)$의 이계도함수라 하고, 기호로 $f^{”}(x)$, $y^{”}$, $\dfrac{d^{2}y}{dx^{2}}$, $\dfrac{d^{2}}{dx^{2}}f(x)$와 같이 나타냅니다.
접선의 방정식
1. 접선의 방정식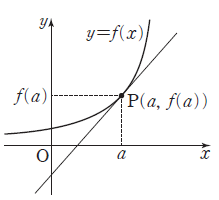
함수 $f(x)$가 $x = a$에서 미분가능할 때, 곡선 $y = f(x)$ 위의 점 $\mathrm{P}(a, f(a))$에서의 접선의 방정식은 $$ y = f^{\prime}(a) (x -\,a) + f(a)$$
2. 접선의 방정식을 구하는 방법
(1) 곡선 $y = f(x)$ 위의 점 $(a, f(a))$에서의 접선의 방정식
① 도함수 $f^{\prime}(x)$에 $x = a$를 대입해서 접선의 기울기 $f^{\prime}(a)$를 구합니다.
② $y = f^{\prime}(a)(x -\,a) + f(a)$에 대입하여 접선의 방정식을 구합니다.
(2) 곡선 $y = f(x)$에 접하고 기울기가 $m$인 접선의 방정식
① 접점의 좌표를 $(t, f(t))$로 놓습니다.
② 방정식 $f^{\prime}(t) = m$을 풀어 접점의 좌표를 구합니다.
③ $y = m(x -\,t) + f(t)$에 대입하여 접선의 방정식을 구합니다.
(3) 곡선 $y = f(x)$ 밖의 한 점 $(\alpha, \beta)$에서 곡선에 그은 접선의 방정식
① 접점의 좌표를 $(t, f(t))$로 놓습니다.
② 접선의 기울기 $f^{\prime}(t)$를 구합니다.
③ 방정식 $\dfrac{f(t) -\,\beta}{t -\,\alpha} = f^{\prime}(t)$를 풀어 $t$의 값을 구합니다.
④ $t$의 값을 $y = f^{\prime}(t)(x -\,t) + f(t)$에 대입하여 접선의 방정식을 구합니다.
(4) 매개변수로 나타낸 곡선 $x = f(t)$, $y = g(t)$에서 $t = a$에 대응하는 점에서의 접선의 방정식
① $t = a$에 대응하는 점의 좌표 $(f(a), g(a))$를 구합니다.
② $\dfrac{g^{\prime}(t)}{f^{\prime}(t)}$를 구한 후 $t = a$에 대응하는 점에서의 접선의 기울기 $\dfrac{g^{\prime}(a)}{f^{\prime}(a)}$의 값을 구합니다.
③ $y = \dfrac{g^{\prime}(a)}{f^{\prime}(a)}\{ x -\,f(a)\} + g(a)$에 대입하여 접선의 방정식을 구합니다.
(5) 곡선 $f(x, y) = 0$ 위의 점 $(a, b)$에서의 접선의 방정식
① 음함수의 미분법을 이용하여 $\dfrac{dy}{dx}$를 구합니다.
② $\dfrac{dy}{dx}$에 $x = a$, $y = b$를 대입하여 접선의 기울기 $m$을 구합니다.
③ $y = m ( x -\,a ) + b$에 대입하여 접선의 방정식을 구합니다.
함수의 그래프
1. 함수의 증가와 감소
(1) 함수의 증가와 감소
함수 $f(x)$가 어떤 구간에 속하는 임의의 두 수 $x_1$, $x_2$에 대하여
① $x_1 \lt x_2$일 때, $f(x_{1}) \lt f(x_{2})$이면 함수 $f(x)$는 이 구간에서 증가한다고 합니다.
② $x_1 \lt x_2$일 때, $f(x_{1}) \gt f(x_{2})$이면 함수 $f(x)$는 이 구간에서 감소한다고 합니다.
(2) 함수의 증가와 감소의 판정
함수 $f(x)$가 어떤 구간에서 미분가능하고, 이 구간의 모든 $x$에 대하여
① $f^{\prime}(x) \gt 0$이면 함수 $f(x)$는 이 구간에서 증가합니다.
② $f^{\prime}(x) \lt 0$이면 함수 $f(x)$는 이 구간에서 감소합니다.
2. 함수의 극대와 극소
(1) 함수의 극대와 극소
함수 $f(x)$가 $x = a$를 포함하는 어떤 열린구간에 속하는 모든 $x$에 대하여
① $f(x) \le f(a)$일 때, 함수 $f(x)$는 $x = a$에서 극대라 하고, $f(a)$를 극댓값이라 합니다.
② $f(x) \ge f(a)$일 때, 함수 $f(x)$는 $x = a$에서 극소라 하고, $f(a)$를 극솟값이라 합니다.
이때 극댓값과 극솟값을 통틀어 극값이라고 합니다.
(2) 도함수를 이용한 함수의 극대와 극소의 판정
미분가능한 함수 $f(x)$에 대하여 $f^{\prime}(a) = 0$이고, $x = a$의 좌우에서 $f^{\prime}(x)$의 부호가
① 음에서 양으로 바뀌면 $f(x)$는 $x = a$에서 극대입니다.
② 양에서 음으로 바뀌면 $f(x)$는 $x = a$에서 극소입니다.
(3) 이계도함수를 이용한 함수의 극대와 극소의 판정
이계도함수를 갖는 함수 $f(x)$에 대하여 $f^{\prime}(a) = 0$일 때
① $f^{”}(a) \lt 0$이면 $f(x)$는 $x = a$에서 극대입니다.
② $f^{”}(a) \gt 0$이면 $f(x)$는 $x = a$에서 극소입니다.
3. 곡선의 오목과 볼록
(1) 곡선의 오목과 볼록
어떤 구간에서 곡선 $y = f(x)$ 위의 임의의 두 점 $\mathrm{P}$, $\mathrm{Q}$에 대하여 이 두 점 사이에 있는
① 곡선 부분이 선분 $\mathrm{PQ}$보다 항상 아래쪽에 있으면
곡선 $y = f(x)$는 이 구간에서 아래로 볼록(또는 위로 오목)하다고 합니다.
② 곡선 부분이 선분 $\mathrm{PQ}$보다 항상 위쪽에 있으면
곡선 $y = f(x)$는 이 구간에서 위로 볼록(또는 아래로 오목)하다고 합니다.
(2) 곡선의 오목과 볼록의 판정
함수 $f(x)$가 어떤 구간에서
① $f^{”}(x) \gt 0$이면 곡선 $y = f(x)$는 이 구간에서 아래로 볼록합니다.
② $f^{”}(x) \lt 0$이면 곡선 $y = f(x)$는 이 구간에서 위로 볼록합니다.
4. 변곡점
(1) 변곡점
곡선 $y = f(x)$ 위의 점 $\mathrm{P}(a, f(a))$에 대하여 $x = a$의 좌우에서 곡선의 모양이 아래로 볼록에서 위로 볼록으로 변하거나 위로 볼록에서 아래로 볼록으로 변할 때, 점 $\mathrm{P}$를 곡선 $y = f(x)$의 변곡점이라 합니다.
(2) 변곡점의 판정
함수 $f(x)$에서 $f^{”}(a) = 0$이고 $x = a$의 좌우에서 $f^{”}(x)$의 부호가 바뀌면 점 $(a, f(a))$는 곡선 $y = f(x)$의 변곡점입니다.
5. 함수의 그래프
함수 $y = f(x)$의 그래프의 개형을 그릴 때에는 다음을 고려해서 그리도록 합니다.
① 함수의 정의역과 치역
② 좌표축과의 교점
③ 극한에 의한 점근선
④ 함수의 증가와 감소, 극대와 극소
⑤ 곡선의 오목과 볼록, 변곡점
함수 $y = f(x)$의 그래프의 점근선은 다음과 같이 극한을 조하사여 파악합니다.
① $\displaystyle \lim_{x \to a-}|\,f(x)\,| = \infty$ 또는 $\displaystyle \lim_{x \to a+}|\,f(x)\,| = \infty$이면 직선 $x = a$가 곡선 $y = f(x)$의 점근선입니다.
② $\displaystyle \lim_{x \to \infty}f(x) = b$ 또는 $\displaystyle \lim_{x \to -\infty}f(x) = b$이면 직선 $y = a$가 곡선 $y = f(x)$의 점근선입니다.
점근선을 파악해서 점근선 근처에서의 곡선의 오목과 볼록을 알 수 있습니다.
방정식과 부등식에의 활용
1. 함수의 최대와 최소
함수 $f(x)$가 닫힌구간 $[\,a,\, b\,]$에서 연속일 때,
구간 $[\,a,\, b\,]$에서의 함수 $f(x)$의 극값, 양 끝 점의 함숫값 $f(a)$, $f(b)$
중에서 가장 큰 값이 $f(x)$의 최댓값이고, 가장 작은 값이 $f(x)$의 최솟값입니다.
2. 방정식의 실근의 개수
(1) 방정식 $f(x) = 0$의 서로 다른 실근의 개수는 함수 $y = f(x)$의 그래프와 $x$축의 교점의 개수와 일치합니다.
(2) 방정식 $f(x) = g(x)$의 서로 다른 실근의 개수는 두 함수 $y = f(x)$, $y = g(x)$의 그래프의 교점의 개수와 일치합니다. 이는 함수 $y = f(x) -\,g(x)$의 그래프와 $x$축의 교점의 개수와도 일치합니다.
3. 부등식에의 활용
(1) 어떤 구간에서 부등식 $f(x) \ge 0$이 성립함을 보이려면
그 구간에서 ($f(x)$의 최솟값)$\ge 0$임을 보이면 됩니다.
(2) 어떤 구간에서 부등식 $f(x) \ge g(x)$이 성립함을 보이려면
$h(x) = f(x) -\,g(x)$로 놓고 그 구간에서 ($h(x)$의 최솟값)$\ge 0$임을 보이면 됩니다.
속도와 가속도
1. 직선 운동에서의 속도와 가속도
수직선 위를 움직이는 점 $\mathrm{P}$의 시각 $t$에서의 위치 $x$가 $x = f(t)$일 때, 점 $\mathrm{P}$의 시각 $t$에서의 속도 $v$와 가속도 $a$는
① $v = \dfrac{dx}{dt} = f^{\prime}(t)$
② $a = \dfrac{dv}{dt} = f^{”}(t)$
2. 평면 운동에서의 속도와 가속도
좌표평면 위를 움직이는 점 $\mathrm{P}$의 시각 $t$에서의 위치 $(x, \,y)$가 $x = f(t)$, $y = g(t)$일 때, 점 $\mathrm{P}$의 시각 $t$에서의 속도와 가속도는
① 속도: $\left( \dfrac{dx}{dt}, \, \dfrac{dy}{dt}\right)$, 즉 $(f^{\prime}(t), \,g^{\prime}(t))$
② 가속도: $\left( \dfrac{d^{2}x}{dt^{2}}, \, \dfrac{d^{2}y}{dt^{2}}\right)$, 즉 $(f^{”}(t), \,g^{”}(t))$
