벡터
람다 $\lambda$의 차례
벡터의 뜻과 연산
1. 벡터의 뜻
(1) 벡터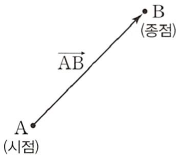
크기와 방향을 함께 갖는 양을 벡터라 하고, 특히 평면 위의 벡터를 평면벡터, 공간에서의 벡터를 공간벡터라 합니다.
(2) 벡터의 표현
방향을 점 $\mathrm{A}$에서 점 $\mathrm{B}$를 향하고 크기가 선분 $\mathrm{AB}$의 길이와 같은 벡터를 그림과 같이 화살표를 사용하여 나타내고, 기호로 $\overrightarrow{\mathrm{AB}}$와 같이 나타냅니다. 이때 점 $\mathrm{A}$를 벡터 $\overrightarrow{\mathrm{AB}}$의 시점, 점 $\mathrm{B}$를 벡터 $\overrightarrow{\mathrm{AB}}$의 종점이라 합니다.
벡터를 한 문자로 나타낼 때는 $\vec{a}$, $\vec{b}$, $\vec{c}$, $\cdots$와 같이 나타냅니다.
(3) 벡터의 크기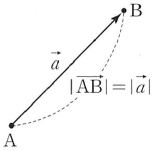
선분 $\mathrm{AB}$의 길이를 벡터 $\overrightarrow{\mathrm{AB}}$의 크기라 하고, 기호로 $|\,\overrightarrow{\mathrm{AB}}\,|$와 같이 나타냅니다. $\vec{a}$의 크기는 $|\,\vec{a}\,|$입니다.
(4) 단위벡터와 영벡터
① 크기가 $1$인 벡터를 단위벡터라 합니다.
② 벡터 $\overrightarrow{\mathrm{AA}}$와 같이 시점과 종점이 일치하는 벡터를 영벡터라 하며, 이것을 기호로 $\vec{0}$와 같이 나타냅니다. 이때 영벡터의 크기는 $0$이고 방향은 생각하지 않습니다.
2. 서로 같은 벡터
(1) 두 벡터 $\vec{a}$, $\vec{b}$의 크기와 방향이 같을 때, 두 벡터는 서로 같다고 하고, 기호로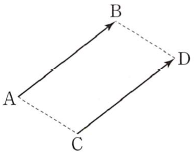
$\vec{a} = \vec{b}$와 같이 나타냅니다.
(2) 두 벡터 $\overrightarrow{\mathrm{AB}}$, $\overrightarrow{\mathrm{CD}}$에 대하여 벡터 $\overrightarrow{\mathrm{AB}}$를 평행이동에 의하여 벡터 $\overrightarrow{\mathrm{CD}}$와 겹칠수 있으면 $\overrightarrow{\mathrm{AB}} = \overrightarrow{\mathrm{CD}}$입니다.
3. 방향이 반대인 벡터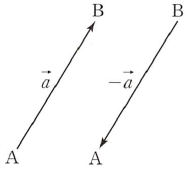
(1) 두 벡터 $\vec{a}$와 크기가 같고 방향이 반대인 벡터를 기호로 $-\vec{a}$와 같이 나타냅니다.
(2) 두 벡터 $\overrightarrow{\mathrm{AB}}$와 $\overrightarrow{\mathrm{BA}}$는 방햐이 반대이고 $|\,\overrightarrow{\mathrm{AB}}\,| = |\,\overrightarrow{\mathrm{BA}}\,|$이므로 $\overrightarrow{\mathrm{AB}} = -\overrightarrow{\mathrm{BA}}$입니다.
4. 벡터의 덧셈
(1) 두 벡터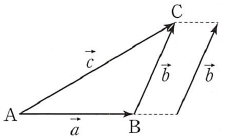
$\vec{a}$, $\vec{b}$에 대하여 벡터 $\vec{a}$의 시점과 종점을 각각 $\mathrm{A}$, $\mathrm{B}$라 하고 $\overrightarrow{\mathrm{BC}} = \vec{b}$가 되는 점 $\mathrm{C}$를 잡습니다. 이때 $\overrightarrow{\mathrm{AC}}$로 나타내어지는 벡터 $\vec{c}$를 벡터 $\vec{a}$와 벡터 $\vec{b}$의 합이라 하고 이것을 기호로 $$\vec{a} + \vec{b} = \vec{c}$$와 같이 나타냅니다. 즉, $\vec{a} = \overrightarrow{\mathrm{AB}}$, $\vec{b} = \overrightarrow{\mathrm{BC}}$일 때, $\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{BC}} = \overrightarrow{\mathrm{AC}}$입니다.
(2) 두 벡터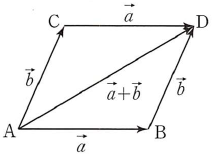
$\vec{a} = \overrightarrow{\mathrm{AB}}$, $\vec{b} = \overrightarrow{\mathrm{AC}}$에 대하여 점 $\mathrm{D}$를 사각형 $\mathrm{ABCD}$가 평행사변형이 되도록 잡으면 $\overrightarrow{\mathrm{AC}} = \overrightarrow{\mathrm{BD}}$이므로 $$\overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{AC}} = \overrightarrow{\mathrm{AB}} + \overrightarrow{\mathrm{BD}} = \overrightarrow{\mathrm{AD}}$$
(3) 벡터의 덧셈에 대한 성질
임의의 세 벡터 $\vec{a}$, $\vec{b}$, $\vec{c}$와 영벡터 $\vec{0}$에 대하여
① 교환법칙: $\vec{a} + \vec{b} = \vec{b} + \vec{a}$
② 결함법칙: $(\vec{a} + \vec{b}) + \vec{c} = \vec{a} + (\vec{b} + \vec{c})$
③ $\vec{a} + \vec{0} = \vec{0} + \vec{a} = \vec{a}$
④ $\vec{a} + (-\vec{a}\,) = (-\vec{a}\,) + \vec{a} = \vec{0}$
5. 벡터의 뺄셈
(1) 두 벡터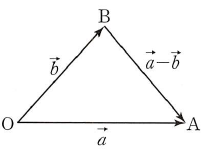
$\vec{a}$, $\vec{b}$에 대하여 $\vec{b} + \vec{x} = \vec{a}$를 만족시키는 벡터 $\vec{x}$를 벡터 $\vec{a}$에서 벡터 $\vec{b}$를 뺀 차라 하고 이것을 기호로 $\vec{x} = \vec{a} -\,\vec{b}$와 같이 나타냅니다. 여기서 $\vec{a} = \overrightarrow{\mathrm{OA}}$, $\vec{b} = \overrightarrow{\mathrm{OB}}$가 되도록 $\mathrm{O}$, $\mathrm{A}$, $\mathrm{B}$를 잡으면 $\overrightarrow{\mathrm{OB}} + \overrightarrow{\mathrm{BA}} = \overrightarrow{\mathrm{OA}}$이므로 $\overrightarrow{\mathrm{BA}} = \overrightarrow{\mathrm{OA}} -\,\overrightarrow{\mathrm{OB}} = \vec{a} -\,\vec{b}$입니다.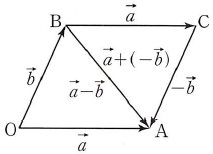
(2) 평행사변형 $\mathrm{OACB}$에서 $\overrightarrow{\mathrm{OA}} = \vec{a}$, $\overrightarrow{\mathrm{OB}} = \vec{b}$일 때, $\vec{a} + (-\vec{b}) = \overrightarrow{\mathrm{OA}} + \overrightarrow{\mathrm{BO}} = \overrightarrow{\mathrm{BO}} + \overrightarrow{\mathrm{OA}} = \overrightarrow{\mathrm{BA}} = \vec{a} -\,\vec{b}$입니다.
6. 벡터의 실수배
(1) 실수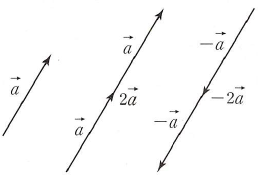
$k$와 벡터 $\vec{a}$에 대하여 벡터 $k\vec{a}$를 벡터 $\vec{a}$의 실수배라 하고 다음과 같이 정의 합니다.
$\vec{a} \ne \vec{0}$일 때
① $k \gt 0$이면 $k\vec{a}$는 벡터 $\vec{a}$와 방향이 같고 크기가 $k|\,\vec{a}\,|$인 벡터입니다.
② $k \lt 0$이면 $k\vec{a}$는 벡터 $\vec{a}$와 방향이 반대이고 크기가 $|\,k\,||\,\vec{a}\,|$인 벡터입니다.
③ $k = 0$이면 $k\vec{a} = \vec{0}$입니다.
$\vec{a} = \vec{0}$일 때 $k\vec{a} = \vec{0}$입니다.
(2) 벡터의 실수배의 성질
두 실수 $k$, $l$과 두 벡터 $\vec{a}$, $\vec{b}$에 대하여
① $k(l\vec{a}) = (kl)\vec{a}$
② $(k + l)\vec{a} = k\vec{a} + l\vec{a}$
③ $k(\vec{a} + \vec{b}) = k\vec{a} + k\vec{b}$
(3) 벡터의 실수배와 단위벡터
영벡터가 아닌 벡터 $\vec{a}$에 대하여 벡터 $\vec{a}$와 방향이 같은 단위벡터는 $\dfrac{\vec{a}}{|\,\vec{a}\,|}$입니다.
7. 벡터의 평행
(1) 영벡터가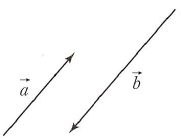
아닌 두 벡터 $\vec{a}$, $\vec{b}$의 방향이 같거나 반대일 때, 두 벡터 $\vec{a}$와 $\vec{b}$는 서로 평행하다고 하고 기호로 $\vec{a}\, // \,\vec{b}$와 같이 나타냅니다.
(2) 영벡터가 아닌 두 벡터 $\vec{a}$, $\vec{b}$에 대하여 $\vec{a}\, // \,\vec{b} \, \Longleftrightarrow \,\vec{b} = k \vec{a}$ (단, $k$는 $0$이 아닌 실수)
(3) 영벡터가 아닌 두 평면벡터 $\vec{a}$, $\vec{b}$가 서로 평행하지 않을 때 $k \vec{a} + l \vec{b} = m \vec{a} + n \vec{b} \, \Longleftrightarrow \, k = m, \,l = n$ (단, $k$, $l$, $m$, $n$은 실수)
특히 $k \vec{a} + l \vec{b} = \vec{0} \, \Longleftrightarrow \, k = 0, \,l = 0$
(4) 서로 다른 세 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에 대하여
세 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$가 한 직선 위에 있다. $\, \Longleftrightarrow \,$ $\overrightarrow{\mathrm{AC}} = k\overrightarrow{\mathrm{AB}}$ (단, $k$는 $0$이 아닌 실수)
평면벡터의 성분과 내적
1. 위치벡터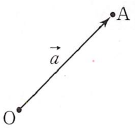
(1) 평면에서 정해진 점 $\mathrm{O}$를 시점으로 하는 벡터 $\overrightarrow{\mathrm{OA}}$를 점 $\mathrm{A}$의 위치벡터라 합니다.
(2) 평면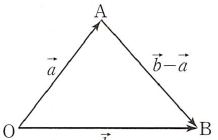
위의 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\overrightarrow{\mathrm{OA}} = \vec{a}$, $\overrightarrow{\mathrm{OB}} = \vec{b}$라 하면 $$\overrightarrow{\mathrm{AB}} = \overrightarrow{\mathrm{OB}} -\,\overrightarrow{\mathrm{OA}} = \vec{b} -\,\vec{a}$$
(3) 내분점의 위치벡터
① 평면에서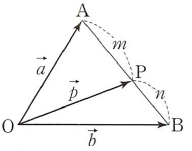
두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$를 $m : n$ ($m \gt 0$, $n \gt 0$)으로 내분하는 점 $\mathrm{P}$의 위치벡터를 $\vec{p}$라 하면 $$\vec{p} = \frac{m\vec{b} + n\vec{a}}{m + n}$$
② 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$의 중점 $\mathrm{M}$의 위치벡터를 $\vec{m}$라 하면 $$\vec{m} = \frac{\vec{a} + \vec{b}}{2}$$
③ 세 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$, $\vec{c}$라 하고, 선분 $\mathrm{ABC}$의 무게중심 $\mathrm{G}$의 위치벡터를 $\vec{g}$라 하면 $$\vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3}$$
(4) 외분점의 위치벡터
두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$를 $m : n$ ($m \gt 0$, $n \gt 0$, $m \ne n$)으로 외분하는 점 $\mathrm{Q}$의 위치벡터를 $\vec{q}$라 하면 $\vec{q} = \dfrac{m\vec{b} -\,n\vec{a}}{m -\,n}$
2. 평면벡터의 성분
좌표평면에서 원점 $\mathrm{O}$를 시점으로 할 때, 점 $\mathrm{A}(a_{1}, a_{2})$의 위치벡터 $\vec{a} = \overrightarrow{\mathrm{OA}}$를 $\vec{a} = (a_{1}, a_{2})$로 나타냅니다. 이때 $a_1$, $a_2$를 평면벡터 $\vec{a}$의 성분이라 하고, $a_1$을 $x$성분, $a_2$를 $y$성분이라고 합니다.
3. 평면벡터의 성분과 연산
두 평면벡터 $\vec{a} = (a_{1}, a_{2})$, $\vec{b} = (b_{1}, b_{2})$에 대하여
① 크기: $|\,\vec{a}\,| = \sqrt{a_{1}^{\,2} + a_{2}^{\,2}}$
② 두 벡터가 서로 같을 조건: $\vec{a} = \vec{b} \,\Longleftrightarrow \,a_{1} = b_{1}, a_{2} = b_{2}$
③ 덧셈과 뺄셈: $\vec{a} + \vec{b} = (a_{1} + b_{1}, \,a_{2} + b_{2})$, $\vec{a} -\,\vec{b} = (a_{1} -\,b_{1}, \,a_{2} -\,b_{2})$
④ 실수배: $k\vec{a} = (ka_{1}, \,ka_{2})$
⑤ 두 점 $\mathrm{A}(a_{1}, a_{2})$, $\mathrm{B}(b_{1}, b_{2})$에 대하여
$\overrightarrow{\mathrm{AB}} = (b_{1} -\,a_{1}, \,b_{2} -\,a_{2})$, $|\,\overrightarrow{\mathrm{AB}}\,| = \sqrt{(b_{1} -\,a_{1})^{2} + (b_{2} -\,a_{2})^{\,2}}$
4. 벡터의 성분과 내적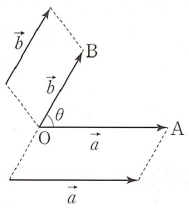
(1) 영벡터가 아닌 두 벡터 $\vec{a}$, $\vec{b}$에 대하여 임의의 한 점 $\mathrm{O}$를 잡아서 $\overrightarrow{\mathrm{OA}} = \vec{a}$, $\overrightarrow{\mathrm{OB}} = \vec{b}$가 되도록 두 점 $\mathrm{A}$, $\mathrm{B}$를 정할 때, $\angle \mathrm{AOB}$의 크기 $\theta$는 점 $\mathrm{O}$의 위치에 관계없이 일정합니다. 이때 $\angle \mathrm{AOB} = \theta$ ($0 \le \theta \le \pi$)를 두 벡터 $\vec{a}$, $\vec{b}$가 이루는 각의 크기라 합니다.
(2) 벡터의 내적
영벡터가 아닌 두 평면벡터 $\vec{a}$, $\vec{b}$가 이루는 각의 크기가 $\theta$ ($0 \le \theta \le \pi$)일 때, $|\,\vec{a}\,||\,\vec{b}\,|\cos \theta$를 두 벡터 $\vec{a}$, $\vec{b}$의 내적이라 하고, 기호로 $\vec{a}\cdot\vec{b}$와 같이 나타냅니다. 즉, $$\vec{a}\cdot\vec{b} = |\,\vec{a}\,||\,\vec{b}\,|\cos \theta$$
(3) 평면벡터의 성분과 내적
두 평면벡터 $\vec{a} = (a_{1}, a_{2})$, $\vec{b} = (b_{1}, b_{2})$에 대하여 $$\vec{a}\cdot\vec{b} = a_{1}b_{1} + a_{2}b_{2}$$
5. 평면벡터의 내적의 성질
(1) 세 평면벡터 $\vec{a}$, $\vec{b}$, $\vec{c}$와 실수 $k$에 대하여
① $\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}$ (교환법칙)
② $\vec{a}\cdot(\vec{b} + \vec{c}) = \vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c}$, $(\vec{a} + \vec{b})\cdot\vec{c} = \vec{a}\cdot\vec{c} + \vec{b}\cdot\vec{c}$ (분배법칙)
③ $(k\vec{a})\cdot\vec{b} = \vec{a}\cdot(k\vec{b}) = k(\vec{a}\cdot\vec{b})$
(2) 평면벡터의 크기와 내적
① $\vec{a}\cdot\vec{a} = |\,\vec{a}\,|^{2}$
② $|\,\vec{a} + \vec{b}\,|^{2} = |\,\vec{a}\,|^{2} + 2\vec{a}\cdot\vec{b} + |\,\vec{b}\,|^{2}$
③ $|\,\vec{a} -\,\vec{b}\,|^{2} = |\,\vec{a}\,|^{2} -\,2\vec{a}\cdot\vec{b} + |\,\vec{b}\,|^{2}$
④ $(\vec{a} + \vec{b})\cdot(\vec{a} -\,\vec{b}) = |\,\vec{a}\,|^{2} -\,|\,\vec{b}\,|^{2}$
6. 두 평면벡터가 이루는 각의 크기
(1) 영벡터가 아닌 두 평면벡터 $\vec{a} = (a_{1}, a_{2})$, $\vec{b} = (b_{1}, b_{2})$가 이루는 각의 크기를 $\theta$ ($0 \le \theta \le \pi$)라 하면 $$\cos \theta = \frac{\vec{a}\cdot\vec{b}}{|\,\vec{a}\,||\,\vec{b}\,|} = \frac{a_{1}b_{1} + a_{2}b_{2}}{\sqrt{a_{1}^{\,2} + a_{2}^{\,2}}\sqrt{b_{1}^{\,2} + b_{2}^{\,2}}}$$
(2) 영벡터가 아닌 두 평면벡터 $\vec{a} = (a_{1}, a_{2})$, $\vec{b} = (b_{1}, b_{2})$에 대하여
① 평행 조건: $\vec{a}\,//\,\vec{b} \Longleftrightarrow \vec{a}\cdot\vec{b} = \pm|\,\vec{a}\,||\,\vec{b}\,| = \pm\sqrt{a_{1}^{\,2} + a_{2}^{\,2}}\sqrt{b_{1}^{\,2} + b_{2}^{\,2}}$
② 수직 조건: $\vec{a} \perp \vec{b} \Longleftrightarrow \vec{a}\cdot\vec{b} = a_{1}b_{1} + a_{2}b_{2} = 0$
공간벡터의 성분과 내적
1. 공간벡터
벡터의 정의는 평면과공간에서 똑같이 적용되는데 이를 구별할 때 평면에서으 벡터를 평면벡터라 하고, 공간에서의 벡터를 공간벡터라 합니다.
2. 위치벡터
(1) 공간에서 정해진 점 $\mathrm{O}$를 시점으로 하는 벡터 $\overrightarrow{\mathrm{OA}}$를 점 $\mathrm{A}$의 위치벡터라 합니다.
(2) 공간에서의 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\overrightarrow{\mathrm{OA}} = \vec{a}$, $\overrightarrow{\mathrm{OB}} = \vec{b}$라 하면 $$\overrightarrow{\mathrm{AB}} = \overrightarrow{\mathrm{OB}} -\,\overrightarrow{\mathrm{OA}} = \vec{b} -\,\vec{a}$$
(3) 내분점의 위치벡터
① 공간에서 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$를 $m : n$ ($m \gt 0$, $n \gt 0$)으로 내분하는 점 $\mathrm{P}$의 위치벡터를 $\vec{p}$라 하면 $$\vec{p} = \frac{m\vec{b} + n\vec{a}}{m + n}$$
② 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$의 중점 $\mathrm{M}$의 위치벡터를 $\vec{m}$라 하면 $$\vec{m} = \frac{\vec{a} + \vec{b}}{2}$$
③ 세 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$, $\vec{c}$라 하고, 선분 $\mathrm{ABC}$의 무게중심 $\mathrm{G}$의 위치벡터를 $\vec{g}$라 하면 $$\vec{g} = \frac{\vec{a} + \vec{b} + \vec{c}}{3}$$
(4) 외분점의 위치벡터
공간에서의 두 점 $\mathrm{A}$, $\mathrm{B}$의 위치벡터를 각각 $\vec{a}$, $\vec{b}$라 하고, 선분 $\mathrm{AB}$를 $m : n$ ($m \gt 0$, $n \gt 0$, $m \ne n$)으로 외분하는 점 $\mathrm{Q}$의 위치벡터를 $\vec{q}$라 하면 $\vec{q} = \dfrac{m\vec{b} -\,n\vec{a}}{m -\,n}$
3. 공간벡터의 성분
(1) 좌표공간에서 원점 $\mathrm{O}$를 시점으로 하고 세 점 $\mathrm{E}_{1}(1, 0, 0)$, $\mathrm{E}_{2}(0, 1, 0)$, $\mathrm{E}_{3}(0, 0, 1)$을 각각 종점으로 하는 세 단위벡터를 $$\overrightarrow{\mathrm{OE}_{1}} = \vec{e_{1}}, \:\overrightarrow{\mathrm{OE}_{2}} = \vec{e_{2}}, \:\overrightarrow{\mathrm{OE}_{3}} = \vec{e_{3}}$$으로 나타냅니다.
(2) 좌표공간에서 원점 $\mathrm{O}$를 시점으로 할 때, 점 $\mathrm{A}(a_{1}, a_{2}, a_{3})$의 위치벡터를 $\vec{a}$라 하면 $$\vec{a} = (a_{1}, a_{2}, a_{3}) = a_{1}\vec{e_{1}} + a_{2}\vec{e_{2}} + a_{3}\vec{e_{3}}$$와 같이 나타낼 수 있습니다.
4. 공간벡터의 크기와 서로 같을 조건
두 공간벡터 $\vec{a} = (a_{1}, a_{2}, a_{3})$, $\vec{b} = (b_{1}, b_{2}, b_{3})$에 대하여
① $|\,\vec{a}\,| = \sqrt{a_{1}^{\,2} + a_{2}^{\,2} + a_{3}^{\,2}}$
② $\vec{a} = \vec{b} \Longleftrightarrow a_{1} = b_{1}, \,a_{2} = b_{2}, \,a_{3} = b_{3}$
5. 공간벡터의 성분에 의한 연산
두 공간벡터 $\vec{a} = (a_{1}, a_{2}, a_{3})$, $\vec{b} = (b_{1}, b_{2}, b_{3})$에 대하여
① $\vec{a} + \vec{b} = (a_{1} + b_{1}, \,a_{2} + b_{2}, \,a_{3} + b_{3})$
② $\vec{a} -\,\vec{b} = (a_{1} -\,b_{1}, a_{2} -\,b_{2}, a_{3} -\,b_{3})$
③ $k\vec{a} = (ka_{1}, ka_{2}, ka_{3})$
6. 두 점에 의한 공간벡터의 성분과 크기
좌표공간의 두 점 $\mathrm{A}(a_{1}, a_{2}, a_{3})$, $\mathrm{B}(b_{1}, b_{2}, b_{3})$에 대하여
① $\overrightarrow{\mathrm{AB}} = (b_{1} -\,a_{1}, b_{2} -\,a_{2}, b_{3} -\,a_{3})$
② $|\,\overrightarrow{\mathrm{AB}}\,| = \sqrt{ (b_{1} -\,a_{1})^{2} + (b_{2} -\,a_{2})^{2} + (b_{3} -\,a_{3})^{2} }$
7. 공간벡터의 내적
(1) 벡터의 내적
영벡터가 아닌 두 공간벡터 $\vec{a}$, $\vec{b}$가 이루는 각의 크기가 $\theta$ ($0 \le \theta \le \pi$)일 때, $\vec{a}$와 $\vec{b}$의 내적 $\vec{a}\cdot\vec{b}$는 평면벡터와 마찬가지로 $\vec{a}\cdot\vec{b} = |\,\vec{a}\,||\,\vec{b}\,|\cos \theta$로 정의합니다.
(2) 공간벡터의 성분과 내적
두 공간벡터 $\vec{a} = (a_{1}, a_{2}, a_{3})$, $\vec{b} = (b_{1}, b_{2}, b_{3})$에 대하여 $\vec{a}\cdot\vec{b} = a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}$입니다.
8. 공간벡터의 내적의 성질
세 공간벡터 $\vec{a}$, $\vec{b}$, $\vec{c}$와 실수 $k$에 대하여
① $\vec{a}\cdot\vec{b} = \vec{b}\cdot\vec{a}$ (교환법칙)
② $\vec{a}\cdot(\vec{b} + \vec{c}) = \vec{a}\cdot\vec{b} + \vec{a}\cdot\vec{c}$, $(\vec{a} + \vec{b})\cdot\vec{c} = \vec{a}\cdot\vec{c} + \vec{b}\cdot\vec{c}$ (분배법칙)
③ $(k\vec{a})\cdot\vec{b} = \vec{a}\cdot(k\vec{b}) = k(\vec{a}\cdot\vec{b})$
9. 두 공간벡터가 이루는 각의 크기
(1) 영벡터가 아닌 두 공간벡터 $\vec{a} = (a_{1}, a_{2}, a_{3})$, $\vec{b} = (b_{1}, b_{2}, b_{3})$가 이루는 각의 크기가 $\theta$ ($0 \le \theta \le \pi$)일 때, $$\cos \theta = \frac{\vec{a}\cdot\vec{b}}{|\,\vec{a}\,||\,\vec{b}\,|} = \frac{a_{1}b_{1} + a_{2}b_{2} + a_{3}b_{3}}{\sqrt{a_{1}^{\,2} + a_{2}^{\,2} + a_{3}^{\,2}}\sqrt{b_{1}^{\,2} + b_{2}^{\,2} + b_{3}^{\,2}}}$$
(2) 영벡터가 아닌 두 평면벡터 $\vec{a} = (a_{1}, a_{2}, a_{3})$, $\vec{b} = (b_{1}, b_{2}, b_{3})$에 대하여
① 평행 조건: $\vec{a}\,//\,\vec{b} \Longleftrightarrow \vec{a}\cdot\vec{b} = \pm|\,\vec{a}\,||\,\vec{b}\,|$
② 수직 조건: $\vec{a} \perp \vec{b} \Longleftrightarrow \vec{a}\cdot\vec{b} = 0$
직선의 방정식
1. 한 점과 방향벡터가 주어진 직선의 방정식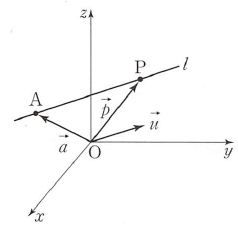
점 $\mathrm{A}(x_{1}, y_{1}, z_{1})$을 지나고 영벡터가 아닌 벡터 $\vec{u} = (a, b, c)$에 평행한 직선의 방정식은 $$x = x_{1} + at, \:y = y_{1} + bt, \:z = z_{1} + ct \:\,(t \textbf{는 실수})$$또는 $$\frac{x -\,x_{1}}{a} = \frac{y -\,y_{1}}{b} = \frac{z -\,z_{1}}{c} \:\,(abc \ne 0)$$입니다. 이때 벡터 $\vec{u} = (a, b, c)$를 이 직선의 방향벡터라 합니다.
2. 두 점을 지나는 직선의 방정식
두 점 $\mathrm{A}(x_{1}, y_{1}, z_{1})$, $\mathrm{ㅠ}(x_{2}, y_{2}, z_{2})$을 지나는 직선의 방정식은 $$\frac{x -\,x_{1}}{x_{2} -\,x_{1}} = \frac{y -\,y_{1}}{y_{2} -\,y_{1}} = \frac{z -\,z_{1}}{z_{2} -\,z_{1}} \:\,(\textbf{단},\:x_{1} \ne x_{2}, y_{1} \ne y_{2}, z_{1} \ne z_{2})$$
3. 두 직선이 이루는 각의 크기
두 직선 $l_{1}$, $l_{2}$의 방향벡터가 각각 $\vec{u_{1}} = (a_{1}, b_{1}, c_{1})$, $\vec{u_{2}} = (a_{2}, b_{2}, c_{2})$일 때, 두 직선 $l_{1}$, $l_{2}$가 이루는 각의 크기를 $\theta$ ($0 \le \theta \le \pi$)라 하면 $$\cos \theta = \frac{\vec{u_{1}}\cdot\vec{u_{2}}}{|\,\vec{u_{1}}\,||\,\vec{u_{2}}\,|} = \frac{a_{1}a_{2} + b_{1}b_{2} + c_{1}c_{2}}{\sqrt{a_{1}^{\,2} + b_{1}^{\,2} + c_{1}^{\,2}}\sqrt{a_{2}^{\,2} + b_{2}^{\,2} + c_{2}^{\,2}}}$$
4. 두 직선의 평행과 수직
두 직선 $l_{1}$, $l_{2}$의 방향벡터가 각각 $\vec{u_{1}} = (a_{1}, b_{1}, c_{1})$, $\vec{u_{2}} = (a_{2}, b_{2}, c_{2})$일 때
① 두 직선 $l_{1}$, $l_{2}$가 서로 평행하면
$l_{1}\,//\,l_{2} \Longleftrightarrow \vec{u_{1}}\,//\,\vec{u_{2}} \Longleftrightarrow \vec{u_{1}} = k\vec{u_{2}} \Longleftrightarrow a_{1} : b_{1} : c_{1} = a_{2} : b_{2} : c_{2}$
② 두 직선 $l_{1}$, $l_{2}$가 서로 수직이면
$l_{1} \perp l_{2} \Longleftrightarrow \vec{u_{1}} \perp \vec{u_{2}} \Longleftrightarrow \vec{u_{1}}\cdot\vec{u_{2}} = a_{1}a_{2} + b_{1}b_{2} + c_{1}c_{2} = 0$
5. 점과 직선 사이의 거리
좌표공간에서 점 $\mathrm{A}$와 직선 $l : \dfrac{x -\,x_{1}}{a} = \dfrac{y -\,y_{1}}{b} = \dfrac{z -\,z_{1}}{c}$ ($abc \neq 0$) 사이의 거리는 다음과 같은 방법으로 구합니다.
① 점 $\mathrm{A}$에서 직선 $l$에 내린 수선의 발을 $\mathrm{H}(x, y, z)$라 하면 $\dfrac{x -\,x_{1}}{a} = \dfrac{y -\,y_{1}}{b} = \dfrac{z -\,z_{1}}{c} = t$에서 $\mathrm{H}(x_{1} + at, y_{1} + bt, z_{1} + ct)$ ($t$는 실수)로 놓습니다.
② 직선 $l$의 방향벡터가 $\vec{u} = (a, b, c)$이고 $\overrightarrow{\mathrm{AH}} \perp \vec{u}$이므로 $\overrightarrow{\mathrm{AH}}\cdot\vec{u} = 0$임을 이용하여 $t$의 값을 구합니다.
③ $t$의 값을 ①에 대입하여 점 $\mathrm{H}$의 좌표를 구한 수, 점 $\mathrm{A}$와 직선 $l$ 사이의 거리인 $|\,\overrightarrow{\mathrm{AH}}\,|$의 값을 구합니다.
평면의 방정식
1. 한 점과 법선벡터가 주어진 평면의 방정식
점 $\mathrm{A}(x_{1}, y_{1}, z_{1})$을 지나고 영벡터가 아닌 벡터 $\vec{n} = (a, b, c)$에 수직인 평면의 방정식은 $$a(x -\,x_{1}) + b(y -\,y_{1}) + c(z -\,z_{1}) = 0$$입니다. 이때 벡터 $\vec{n} = (a, b, c)$을 이 평면의 법선벡터라고 합니다.
2. 일차방정식과 평면
좌표공간에서 $x$, $y$, $z$에 대한 일차방정식 $$ax + by + cz = 0$$은 법선벡터가 $\vec{n} = (a, b, c)$인 평면을 나타냅니다.
3. 두 평면이 이루는 각의 크기
두 평면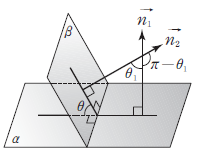
$\alpha$, $\beta$의 법선벡터가 각각 $\vec{n_{1}} = (a_{1}, b_{1}, c_{1})$, $\vec{n_{2}} = (a_{2}, b_{2}, c_{2})$일 때, 두 평면 $\alpha$, $\beta$가 이루는 각의 크기를 $\theta$ ($0 \le \theta \le \frac{\pi}{2}$)라 하면 $$\cos \theta = \frac{\vec{n_{1}}\cdot\vec{n_{2}}}{|\,\vec{n_{1}}\,||\,\vec{n_{2}}\,|} = \frac{a_{1}a_{2} + b_{1}b_{2} + c_{1}c_{2}}{\sqrt{a_{1}^{\,2} + b_{1}^{\,2} + c_{1}^{\,2}}\sqrt{a_{2}^{\,2} + b_{2}^{\,2} + c_{2}^{\,2}}}$$
4. 두 평면의 평행과 수직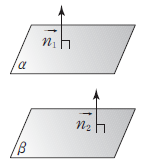
두 평면 $\alpha$, $\beta$의 법선벡터가 각각 $\vec{n_{1}} = (a_{1}, b_{1}, c_{1})$, $\vec{n_{2}} = (a_{2}, b_{2}, c_{2})$일 때
① 두 평면 $\alpha$, $\beta$가 서로 평행하면
$\alpha\,//\,\beta \Longleftrightarrow \vec{n_{1}}\,//\,\vec{n_{2}} \Longleftrightarrow \vec{n_{1}} = k\vec{n_{2}} \Longleftrightarrow a_{1} : b_{1} : c_{1} = a_{2} : b_{2} : c_{2}$
② 두 평면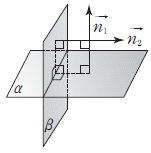
$\alpha$, $\beta$가 서로 수직이면
$\alpha \perp \beta \Longleftrightarrow \vec{n_{1}} \perp \vec{n_{2}} \Longleftrightarrow \vec{n_{1}}\cdot\vec{n_{2}} = a_{1}a_{2} + b_{1}b_{2} + c_{1}c_{2} = 0$
5. 점과 평면 사이의 거리
점 $(x_{1}, y_{1}, z_{1})$과 평면 $ax + by + cz = 0$ 사이의 거리는 $$\frac{|\,ax_{1} + by_{1} + cz_{1}\,|}{\sqrt{a^{2} + b^{2} + c^{2}}}$$
구의 방정식
1. 벡터로 나타낸 구의 방정식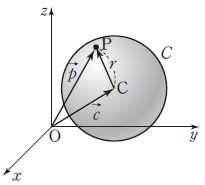
중심이 $\mathrm{C}$이고 반지름의 길이가 $r$인 구 위의 임의의 점을 $\mathrm{P}$라 하고 두 점 $\mathrm{C}$, $\mathrm{P}$의 위치벡터를 각각 $\vec{c}$, $\vec{p}$라 하면 구의 벡터방정식은 $$|\,\vec{p} -\,\vec{c}\,| = r \,\textbf{ 또는 } \,(\vec{p} -\,\vec{c})\cdot(\vec{p} -\,\vec{c}) = r^{2}$$
2. 좌표공간에서의 구의 방정식
중심이 점 $\mathrm{C}(a, b, c)$이고 반지름의 길이가 $r$인 구의 방정식은 $$(x -\,a)^{2} + (y -\,b)^{2} + (z -\,c)^{2} = r^{2}$$