삼각함수
람다 $\lambda$의 차례
일반각과 호도법
1. 일반각
(1) 시초선과 동경
두 반직선 $\mathrm{OX}$, $\mathrm{OP}$에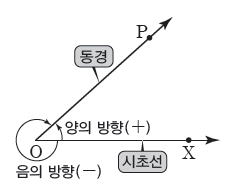
의하여 정해진 $\angle \mathrm{XOP}$의 크기는 반직선 $\mathrm{OP}$가 점 $\mathrm{O}$를 중심으로 고정된 반직선 $\mathrm{OX}$의 위치에서 반직선 $\mathrm{OP}$의 위치까지 회전한 양입니다. 이때 반직선 $\mathrm{OX}$를 시초선, 반직선 $\mathrm{OP}$를 동경이라고 합니다.
(2) 일반각
시초선 $\mathrm{OX}$와 동경 $\mathrm{OP}$가 나타내는 한 각의 크기를 $\alpha^{\circ}$라 하면 $\angle \mathrm{XOP} = 360^{\circ} \times n + \alpha^{\circ}$ ($n$은 정수) 꼴로 나타낼 수 있고, 이것을 동경 $\mathrm{OP}$가 나타내는 일반각이라고 합니다.
(3) 사분면의 각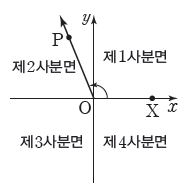
좌표평면에서 시초선을 원점 $\mathrm{O}$에서 $x$축 양의 방향으로 잡을 때, 제$1$사분면, 제$2$사분면, 제$3$사분면, 제$4$사분면에 있는 동경 $\mathrm{OP}$가 나타내는 각을 각각 제$1$사분면의 각, 제$2$사분면의 각, 제$3$사분면의 각, 제$4$사분면의 각이라고 합니다.
2. 호도법
(1) $1$라디안
반지름의 길이가 $r$인 원에서 길이가 $$r인 호에 대한 중심각의 크기를 $1$라디안이라고 합니다.
(2) 호도법
라디안으로 각의 크기를 나타내는 방법을 호도법이라고 합니다.
$1$라디안$= \left( \frac{180}{\pi} \right)^{\circ}$
$1^{\circ} = \frac{\pi}{180}$라디안
3. 부채꼴의 호의 길이와 넓이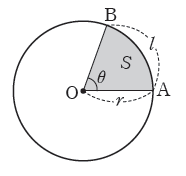
반지름의 길이가 $r$, 중심각의 크기가 $\theta$ (라디안)인 부채꼴의 호의 길이를 $l$, 넓이를 $S$라 하면 $$l = r \theta, \:S = \frac{1}{2}r^{2}\theta = \frac{1}{2}rl$$
삼각함수의 뜻
1. 삼각함수
좌표평면에서 시초선을 원점 $\mathrm{O}$에서 $x$축 양의 방향으로 잡을 때, 각 $\theta$를 나타내는 동경과 원점 $\mathrm{O}$를 중심으로 하고 반지름의 길이가 $r$인 원의 교점을 $\mathrm{P}(x, \,y)$라 하면 $$\cos \theta =
\frac{x}{r},\: \sin \theta = \frac{y}{r}, \:\tan \theta = \frac{y}{x}\: (x \ne 0)$$이들 함수를 차례로 $\theta$에 대한 코사인함수, 사인함수, 탄젠트함수라 하고 이 함수들을 $\theta$에 대한 삼각함수라고 합니다.
단위원과 동경 $\theta$가 만나는 교점의 좌표가 $(\cos \theta, \,\sin \theta)$입니다. 즉 단위원과 동경 $\theta$가 만나는교점의 $x$좌표가 $\cos \theta$, 단위원과 동경 $\theta$가 만나는 교점의 $y$좌표가 $\sin \theta$이고, 동경 $\theta$의 기울기가 $\tan \theta$입니다.
2. 삼각함수의 값의 부호
삼각함수의 값의 부호는 각 $$가 제몇사분면의 각인지에 따라 다음과 같이 정해집니다.
3. 삼각함수 사이의 관계
① $\tan \theta$는 동경 $\theta$의 기울기: $\tan \theta = \dfrac{\sin \theta}{\cos \theta}$
② $(\cos \theta, \sin \theta)$는 단위원 위의 점: $\cos^{2}\theta + \sin^{2}\theta = 1$
삼각함수의 그래프
1. 주기함수
함수 $f$의 정의역에 속하는 모든 실수 $x$에 대하여 $$f(x+p) = f(x)$$를 만족시키는 $0$이 아닌 상수 $p$가 존재할 때, 함수 $f$를 주기함수라 하고, 이러한 상수 $p$ 중에서 최소인 양수를 그 함수의 주기라고 합니다.
2. 함수 $y = \sin x$의 성질
① 정의역: 실수 전체의 집합
② 치역: $\{\,y\,|-1 \le x \le 1 \}$
③ $y = \sin x$의 그래프는 원점에 대하여 대칭. 즉 $\sin(-x) = – \sin x$
④ 주기가 $2\pi$인 주기함수. 즉 $\sin (2n\pi + x) = \sin x$ ($n$은 정수)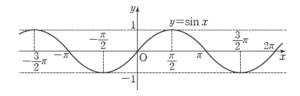
3. 함수 $y = \cos x$의 성질
① 정의역: 실수 전체의 집합
② 치역: $\{\,y\,|-1 \le x \le 1 \}$
③ $y = \cos x$의 그래프는 $y$축에 대하여 대칭. 즉 $\cos(-x) = \cos x$
④ 주기가 $2\pi$인 주기함수. 즉 $\cos (2n\pi + x) = \cos x$ ($n$은 정수)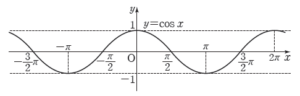
4. 함수 $y = \tan x$의 성질
① 정의역: $x \ne n \pi + \dfrac{\pi}{2}$ ($n$은 정수)인 실수 전체의 집합
② 치역: 실수 전체의 집합
③ 그래프의 점근선은 직선 $x = n \pi + \dfrac{\pi}{2}$ ($n$은 정수)
④ 그래프는 원점에 대하여 대칭. 즉 $\tan (-x) = – \tan x$
⑤ 주기가 $\pi$인 주기함수. 즉 $\tan (n \pi + x) = \tan x$ ($n$은 정수)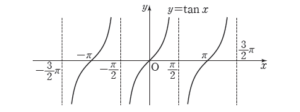
5. 삼각함수의 최대 최소와 주기
① 함수 $y = a \sin (bx + c) + d$의 최댓값은 $|\,a\,| + b$, 최솟값은 $-|\,a\,| + b$, 주기는 $\dfrac{2 \pi}{|\,b\,|}$
② 함수 $y = a \cos (bx + c) + d$의 최댓값은 $|\,a\,| + b$, 최솟값은 $-|\,a\,| + b$, 주기는 $\dfrac{2 \pi}{|\,b\,|}$
③ 함수 $y = a \tan (bx + c) + d$의 최댓값은 없고, 최솟값도 없고, 주기는 $\dfrac{\pi}{|\,b\,|}$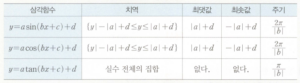
6. 여러 가지 각에 대한 삼각함수의 성질
(1) $2n \pi + \theta$의 삼각함수 (단, $n$은 정수)
① $\sin (2n \pi + \theta) = \sin \theta$
② $\cos (2n \pi + \theta) = \cos \theta$
③ $\tan (2n \pi + \theta) = \tan \theta$
(2) $- \theta$의 삼각함수
① $\sin (- \theta) = – \sin \theta$
② $\cos (- \theta) = \cos \theta$
③ $\tan (- \theta) = – \tan \theta$
(3) $\pi \pm \theta$의 삼각함수
① $\sin (\pi \pm \theta) = \mp \sin \theta$ (부호는 순서대로)
② $\cos (\pi \pm \theta) = – \cos \theta$
③ $\tan (\pi \pm \theta) = \pm \tan \theta$ (부호는 순서대로)
(4) $\dfrac{\pi}{2} \pm \theta$의 삼각함수
① $\sin (\frac{\pi}{2} \pm \theta) = \cos \theta$
② $\cos (\frac{\pi}{2} \pm \theta) = \mp \sin \theta$ (부호는 순서대로)
③ $\tan (\frac{\pi}{2} \pm \theta) = \mp \dfrac{1}{\tan \theta}$ (부호는 순서대로)
7. 삼각방정식과 삼각부등식
(1) 삼각방정식의 풀이
① 주어진 방정식을 $\sin x = k$ 또는 $\cos x = k$ 또는 $\tan x = k$ 꼴로 고칩니다.
② 함수 $y = \sin x$ 또는 $y = \cos x$ 또는 $y = \tan x$의 그래프와 직선 $y = k$의 교점의 $x$좌표를 찾아 방정식의 해을 구합니다.
(2) 삼각부등식의 풀이
① $\sin x \gt k$ 또는 $\cos x \gt k$ 또는 $\tan x \gt k$ 꼴의 해
함수 $y = \sin x$ 또는 $y = \cos x$ 또는 $y = \tan x$의 그래프가 직선 $y = k$ 보다 위쪽에 있는 $x$의 값의 범위를 구합니다.
② $\sin x \lt k$ 또는 $\cos x \lt k$ 또는 $\tan x \lt k$ 꼴의 해
함수 $y = \sin x$ 또는 $y = \cos x$ 또는 $y = \tan x$의 그래프가 직선 $y = k$ 보다 아래쪽에 있는 $x$의 값의 범위를 구합니다.
사인법칙
1. 사인법칙
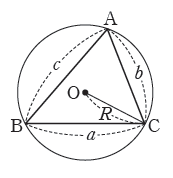삼각형 $\mathrm{ABC}$의 외접원의 반지를의 길이을 $R$라 하면 $$\dfrac{a}{\sin A} = \dfrac{b}{\sin B} = \dfrac{c}{\sin C} = 2R$$ (단, 삼각형 $\mathrm{ABC}$에서 $\angle \mathrm{A}$, $\angle \mathrm{B}$, $\angle \mathrm{C}$의 크기를 각각 $A$, $B$, $C$로 나타내고 이들의 대변의 길이를 각각 $a$, $b$, $c$로 나타냅니다.)
2. 사인법칙의 변형
① $\sin A = \dfrac{a}{2R}$, $\sin B = \dfrac{b}{2R}$, $\sin C = \dfrac{c}{2R}$
② $a = 2R \sin A$, $b = 2R \sin B$, $c = 2R \sin C$
③ $R = \dfrac{a}{2 \sin A} = \dfrac{b}{2 \sin B} = \dfrac{c}{2 \sin C} $
④ $a : b : c = \sin A : \sin B : \sin C$
코사인법칙
1. 코사인법칙
삼각형 $\mathrm{ABC}$에서
$$a^{2} = b^{2} + c^{2} -\, 2bc \cos A$$ $$b^{2} = c^{2} + a^{2} -\, 2ca \cos B$$ $$c^{2} = a^{2} + b^{2} -\, 2ab \cos C$$
(단, 삼각형 $\mathrm{ABC}$에서 $\angle \mathrm{A}$, $\angle \mathrm{B}$, $\angle \mathrm{C}$의 크기를 각각 $A$, $B$, $C$로 나타내고 이들의 대변의 길이를 각각 $a$, $b$, $c$로 나타냅니다.)
2. 코사인법칙의 변형
삼각형 $\mathrm{ABC}$에서
$$\cos A = \dfrac{b^{2} + c^{2} -\, a^{2} }{2bc}$$ $$\cos B = \dfrac{c^{2} + a^{2} -\, b^{2} }{2ca}$$ $$\cos C = \dfrac{a^{2} + b^{2} -\, c^{2} }{2ab}$$
삼각형의 넓이
1. 삼각형의 넓이
(1) 삼각형 $\mathrm{ABC}$의 넓이를 $S$라 하면
$S = \dfrac{1}{2}bc \sin A = \dfrac{1}{2}ca \sin B = \dfrac{1}{2}ab \sin C$
(2) 삼각형 $\mathrm{ABC}$의 넓이를 $S$, 외접원의 반지름의 길이를 $R$라 하면
$S = \dfrac{abc}{4R} = 2R^{2} \sin A \sin B \sin C$
(3) 삼각형 $\mathrm{ABC}$의 넓이를 $S$, 외접원의 반지름의 길이를 $R$, 내접원의 반지름의 길이를 $r$라 하면
$R = \dfrac{abc}{4S}$
$r = \dfrac{S}{s}$ (단, $s = \frac{a + b + c}{2}\,$)
2. 사각형의 넓이
(1) 평행사변형의 넓이
평행사변형 $\mathrm{ABCD}$에서 이웃하는 두 변의 길이가 $a$, $b$이고 그 끼인각의 크기가 $\theta$일 때, 평행사변형 $\mathrm{ABCD}$의 넓이를 $S$라 하면
$S = ab \sin \theta$
(2) 사각형의 넓이
사각형 $\mathrm{ABCD}$에서 두 대각선의 길이가 $p$, $q$이고 두 대각선이 이루는 각의 크기가 $\theta$일 때, 사각형 $\mathrm{ABCD}$의 넓이를 $S$라 하면
$S = \dfrac{1}{2}pq \sin \theta$