이차곡선
람다 $\lambda$의 차례
포물선
1. 포물선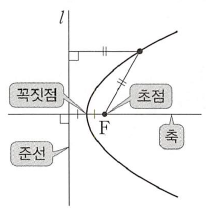
평면 위의 한 점 $\mathrm{F}$와 이 점을 지나지 않는 한 직선 $l$이 주어질 때, 점 $\mathrm{F}$와 직선 $l$에 이르는 거리가 각각 같은 점들의 집합을 포물선이라 하고, 점 $\mathrm{F}$를 포물선의 초점, 직선 $l$을 포물선의 준선이라 합니다.
이때 포물선의 초점 $\mathrm{F}$을 지나고 준선 $l$에 수직인 직선을 포물선의 축, 포물선과 축의 교점을 포물선의 꼭짓점이라고 합니다.
2. 포물선의 방정식
① 초점이 점 $\mathrm{F}(p, 0)$이고 준선의 방정식이 $x = -p$인 포물선의 방정식은 $$y^{2} = 4px\:\, (\textbf{단, }p \ne 0)$$
② 초점이 점 $\mathrm{F}(0, p)$이고 준선의 방정식이 $y = -p$인 포물선의 방정식은 $$x^{2} = 4py\:\, (\textbf{단, }p \ne 0)$$
3. 포물선의 평행이동
포물선 $y^{2} = 4px$를 $$축의 방향으로 $$만큼, $$축의 방향으로 $$만큼 평행이동한 포물선의 방정식은 $(y -\,n)^{2} = 4p(x -\,m)$
타원
1. 타원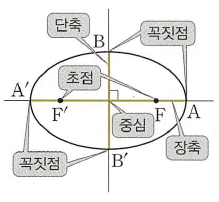
평면 위의 서로 다른 두 점 $\mathrm{F}$, $\mathrm{F}’$에서의 거리의 합이 일정한 점들의 집합을 타원이라 하고, 두 점 $\mathrm{F}$, $\mathrm{F}’$을 타원의 초점이라 합니다.
두 초점 $\mathrm{F}$, $\mathrm{F}’$을 잇는 직선이 타원과 만나는 두 점을 각각 $\mathrm{A}$, $\mathrm{A}’$, $\overline{\mathrm{FF’}}$의 수직이등분선이 타원과 만나는 두 점을 각각 $\mathrm{B}$, $\mathrm{B}’$이라 할 때, 네 점 $\mathrm{A}$, $\mathrm{A}’$, $\mathrm{B}$, $\mathrm{B}’$을 타원의 꼭짓점, $\overline{\mathrm{AA’}}$을 타원의 장축, $\overline{\mathrm{BB’}}$을 타원의 단축, 장축과 단축의 교점을 타원의 중심이라고 합니다.
2. 타원의 방정식
(1) 두 초점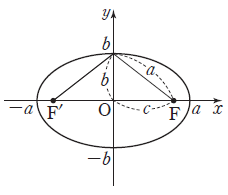
$\mathrm{F}(c, \,0)$, $\mathrm{F’}(-c, \,0)$에서의 거리의 합이 $2a$ ($a \gt c \gt 0$)인 타원의 방정식은 $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\:\, (\textbf{단},\text{ }b \gt 0,\, b^{2} = a^{2} -\,c^{2})$$
① 장축의 길이: $2a$, 단축의 길이: $2b$
② 초점의 좌표: $\mathrm{F}(\sqrt{a^{2} -\,b^{2}}, \,0)$, $\mathrm{F’}(-\sqrt{a^{2} -\,b^{2}}, \,0)$
③ 꼭짓점의 좌표: $(a, \,0)$, $(-a, \,0)$, $(0, \,b)$, $(0, \,-b)$
(2) 두 초점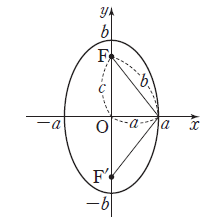
$\mathrm{F}(0, \,c)$, $\mathrm{F’}(0, \,-c)$에서의 거리의 합이 $2b$ ($b \gt c \gt 0$)인 타원의 방정식은 $$\frac{x^2}{a^2} + \frac{y^2}{b^2} = 1\:\, (\textbf{단},\text{ }a \gt 0,\, a^{2} = b^{2} -\,c^{2})$$
① 장축의 길이: $2b$, 단축의 길이: $2a$
② 초점의 좌표: $\mathrm{F}(0, \,\sqrt{b^{2} -\,a^{2}})$, $\mathrm{F’}(0, \,-\sqrt{b^{2} -\,a^{2}})$
③ 꼭짓점의 좌표: $(a, \,0)$, $(-a, \,0)$, $(0, \,b)$, $(0, \,-b)$
3. 타원의 평행이동
타원 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$을 $x$축의 방향으로 $m$만큼, $y$축의 방향으로 $n$만큼 평행이동한 타원의 방정식은 $\dfrac{(x -\,m)^2}{a^2} + \dfrac{(y -\,n)^2}{b^2} = 1$
쌍곡선
1. 쌍곡선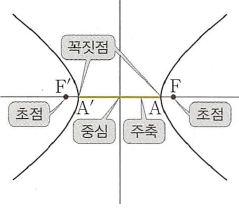
평면 위의 서로 다른 두 점 $\mathrm{F}$, $\mathrm{F’}$에서의 거리의 차가 일정한 점들의 집합을 쌍곡선이라 하고, 두 점 $\mathrm{F}$, $\mathrm{F’}$을 쌍곡선의 초점이라 합니다.
두 초점 $\mathrm{F}$, $\mathrm{F’}$을 잇는 직선이 쌍곡선과 만나는 두 점을 각각 $\mathrm{A}$, $\mathrm{A’}$이라 할 때, 두 점 $\mathrm{A}$, $\mathrm{A’}$을 쌍곡선의 꼭짓점, $\overline{\mathrm{AA’}}$을 쌍곡선의 주축, $\overline{\mathrm{AA’}}$의 중점을 쌍곡선의 중심이라고 합니다.
2. 쌍곡선의 방정식
(1) 두 초점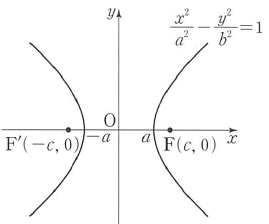
$\mathrm{F}(c, \,0)$, $\mathrm{F’}(-c, \,0)$에서의 거리의 차가 $2a$ ($c \gt a \gt 0$)인 쌍곡선의 방정식은 $$\frac{x^2}{a^2} -\,\frac{y^2}{b^2} = 1\:\, (\textbf{단},\text{ }b \gt 0,\, b^{2} = c^{2} -\,a^{2})$$
① 주축의 길이: $2a$
② 초점의 좌표: $\mathrm{F}(\sqrt{a^{2} + b^{2}}, \,0)$, $\mathrm{F’}(-\sqrt{a^{2} + b^{2}}, \,0)$
③ 꼭짓점의 좌표: $(a, \,0)$, $(-a, \,0)$
(2) 두 초점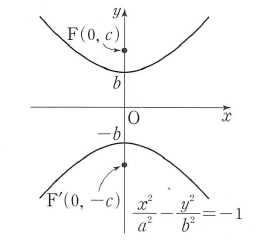
$\mathrm{F}(0, \,c)$, $\mathrm{F’}(0, \,-c)$에서의 거리의 차가 $2b$ ($c \gt b \gt 0$)인 쌍곡선의 방정식은 $$\frac{x^2}{a^2} -\,\frac{y^2}{b^2} = -1\:\, (\textbf{단},\text{ }a \gt 0,\, a^{2} = c^{2} -\,b^{2})$$
① 주축의 길이: $2b$
② 초점의 좌표: $\mathrm{F}(0, \,\sqrt{b^{2} + a^{2}})$, $\mathrm{F’}(0, \,-\sqrt{b^{2} + a^{2}})$
③ 꼭짓점의 좌표: $(0, \,b)$, $(0, \,-b)$
3. 쌍곡선의 평행이동
쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = 1$을 $x$축의 방향으로 $m$만큼, $y$축의 방향으로 $n$만큼 평행이동한 쌍곡선의 방정식은 $\dfrac{(x -\,m)^2}{a^2} -\,\dfrac{(y -\,n)^2}{b^2} = 1$
4. 쌍곡선의 점근선
쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = 1$와 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = -1$의 점근선의 방정식은 $y = \pm \dfrac{b}{a}x$
이차곡선의 접선
1. 이차곡선
(1) 계수가 실수인 두 일차식의 곱으로 인수분해되지 않는 $x$, $y$에 대한 이차방정식
$Ax^{2} + By^{2} + Cxy + Dx +Ey +F = 0$ ($A$, $B$, $C$, $D$, $E$, $F$는 상수)
이 나타내는 곡선을 이차곡선이라 합니다.
(2) 원, 포물선, 타원, 쌍곡선은 모두 이차곡선입니다. 특히 위의 이차방정식에서 $C = 0$일 때, 계수의 조건에 따라 이차방정식은 다음과 같이 원, 포물선, 타원, 쌍곡선 중 하나로 나타납니다.
① $A = B$, $AB \ne 0$이면 원
② ($A = 0$, $BD \ne 0$) 또는 ($B = 0$, $AE \ne 0$)이면 포물선
③ $AB \gt 0$, $A \ne B$이면 타원
④ $AB \lt 0$이면 쌍곡선
2. 이차곡선과 직선의 위치 관계
이차곡선의 방정식과 직선의 방정식에서 한 문자를 소거하여 얻은 이차방정식의 판별식을 $D$라 하면 $D$의 부호를 알아내서 이차곡선과 직선의 위치 관계를 알 수 있습니다.
① $D \gt 0$ $\Longleftrightarrow$ 서로 다른 두 점에서 만난다.
② $D = 0$ $\Longleftrightarrow$ 한 점에서 만난다. (접한다.)
③ $D \lt 0$ $\Longleftrightarrow$ 만나지 않는다.
3. 이차곡선의 접선의 방정식
(1) 포물선의 접선의 방정식
① 포물선 $y^{2} = 4px$에 접하고 기울기 $m$ ($m \ne 0$)인 직선의 방정식은 $$y = mx + \frac{p}{m}$$
② 포물선 $y^{2} = 4px$ 위의 점 $(x_{1}, \,y_{1})$에서의 접선의 방정식은 $$y_{1}y = 2p(x + x_{1})$$
(2) 타원의 접선의 방정식
① 타원 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$에 접하고 기울기 $m$인 직선의 방정식은 $$y = mx \pm \sqrt{a^{2}m^{2} + b^{2}}$$
② 타원 $\dfrac{x^2}{a^2} + \dfrac{y^2}{b^2} = 1$ 위의 점 $(x_{1}, \,y_{1})$에서의 접선의 방정식은 $$\frac{x_{1}x}{a^2} + \frac{y_{1}y}{b^2} = 1$$
(3) 쌍곡선의 접선의 방정식
① 쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = 1$에 접하고 기울기 $m$인 직선의 방정식은 $$y = mx \pm \sqrt{a^{2}m^{2} -\,b^{2}}\:\, (\textbf{단},\text{ }a^{2}m^{2} -\,b^{2} \gt 0\,)$$ 쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = -1$에 접하고 기울기 $m$인 직선의 방정식은 $$y = mx \pm \sqrt{b^{2} -\,a^{2}m^{2}}\:\, (\textbf{단},\text{ }b^{2} -\,a^{2}m^{2} \gt 0\,)$$
② 쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = 1$ 위의 점 $(x_{1}, \,y_{1})$에서의 접선의 방정식은 $$\frac{x_{1}x}{a^2} -\,\frac{y_{1}y}{b^2} = 1$$