적분법
람다 $\lambda$의 차례
여러 가지 함수의 적분법
1. 함수 $y = x^{n}$의 부정적분
실수 $n$에 대하여
① $n \ne -1$일 때, $\displaystyle \int x^{n} dx = \dfrac{1}{n + 1}x^{n + 1} + C$
② $n = -1$일 때, $\displaystyle \int x^{-1} dx = \int \dfrac{1}{x} dx = \ln |\,x\,| + C$
2. 지수함수의 부정적분
① $\displaystyle \int e^{x} dx = e^{x} + C$
② $\displaystyle \int a^{x} dx = \dfrac{a^{x}}{\ln a} + C$ (단, $a \gt 0$, $a \ne 1\,$)
3. 삼각함수의 부정적분
① $\displaystyle \int \sin x dx = – \cos x + C$
② $\displaystyle \int \cos x dx = \sin x + C$
③ $\displaystyle \int \sec^{2} x dx = \tan x + C$
④ $\displaystyle \int \csc^{2}x dx = – \cot x + C$
⑤ $\displaystyle \int \sec x \tan x dx = \sec x + C$
⑥ $\displaystyle \int \csc x \cot x dx = \csc x + C$
$\tan^{2} x$, $\cot^{2} x$의 부정적분을 구할 때는 $\tan^{2} x + 1 = \sec^{2} x$, $1 + \cot^{2} x = \csc^{2} x$를 이용하여 피적분함수를 변형한 후에 적분합니다.
치환적분법
1. 치환적분법
(1) 치환적분법
미분가능한 함수 $g(t)$에 대하여 $x = g(t)$로 놓으면 $$\int f(x) dx = \int f(g(t)) g^{\prime}(t) dt$$
(2) 피적분함수가 $f(g(x))g^{\prime}(x)$ 꼴인 경우에는 $g(x) = t$로 놓으면 $g^{\prime}(x) = \dfrac{dt}{dx}$이므로 $\displaystyle \int f(g(x)) g^{\prime}(x) dx = \int f(t) dt$
일반적으로 치환대상의 미분 꼴이 곱해져 있을 때, 치환적분을 사용합니다.
(3) 피적분함수가 $f(ax+b)$ 꼴인 경우에는 $\displaystyle \int f(x) dx = F(x) + C$이면 $\displaystyle \int f(ax + b) dx = \frac{1}{a} F(ax + b) + C$ (단, $a \ne 0$)
2. $\displaystyle \int \frac{f^{\prime}(x)}{f(x)}dx$ 꼴의 부정적분
$$\int \frac{f^{\prime}(x)}{f(x)}dx = \ln |\,f(x)\,| + C$$
3. 유리함수의 부정적분
(1) (분자의 차수)$\,\ge\,$(분모의 차수)인 경우
분자를 분모로 나누어 몫과 나머지의 꼴로 나타내어 부정적분을 구합니다.
(2) (분자의 차수)$\,\lt\,$(분모의 차수)인 경우
부분분수로 변형하여 부정적분을 구합니다.
① $\dfrac{1}{(x + a)(x + b)} = \dfrac{1}{b -\,a}\left( \dfrac{1}{x + a} -\,\dfrac{1}{x + b} \right)$ (단, $a \ne b\,$)
② $\dfrac{px + q}{(x + a)(x + b)} = \dfrac{A}{x + a} -\,\dfrac{B}{x + b}$ (항등식임을 이용하여 $A$, $B$의 값을 구합니다.)
부분적분법
1. 부분적분법
(1) 부분적분법
두 함수 $f(x)$, $g(x)$가 미분가능할 때, $$\int f(x)g^{\prime}(x) dx = f(x)g(x) -\,\int f^{\prime}(x)g(x) dx$$
(2) 부분적분법에 의한 로그함수의 적분: $\displaystyle \int \ln x\, dx = x \ln x -\,x + C$
정적분
1. 정적분
(1) 함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, $f(x)$의 한 부정적분을 $F(x)$라 하면 $f(x)$의 $a$에서 $b$까지의 정적분은 $$\int_{a}^{b}f(x) dx = \Bigg[ F(x) \Bigg]_{a}^{b} = F(b) -\, F(a)$$
(2) $\displaystyle \int_{a}^{a}f(x) dx = 0$
$\displaystyle \int_{a}^{b}f(x) dx = – \int_{b}^{a}f(x) dx $
2. 정적분의 성질
두 함수 $f(x)$, $g(x)$가 세 실수 $a$, $b$, $c$를 포함하는 구간에서 연속일 때
① $\displaystyle \int_{a}^{b}k f(x) dx = k \int_{a}^{b} f(x) dx$
② $\displaystyle \int_{a}^{b} \{ f(x) \pm g(x) \} dx = \int_{a}^{b} f(x) dx \pm \int_{a}^{b} g(x) dx$ (복호동순)
③ $\displaystyle \int_{a}^{b} f(x) dx = \int_{a}^{c} f(x) dx + \int_{c}^{b} f(x) dx$
3. 짝함수$\cdot$홀함수의 정적분
함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 이 구간의 모든 $x$에 대하여
① $f(x)$가 $y$축에 대칭인 함수, 즉 $f(-x) = f(x)$이면 $\displaystyle \int_{-a}^{a}f(x) dx = 2\int_{-a}^{0}f(x) dx = 2\int_{0}^{a}f(x) dx$
② $f(x)$가 원점에 대칭인 함수, 즉 $f(-x) = -f(x)$이면 $\displaystyle \int_{-a}^{a}f(x) dx = 0$
4. 주기함수의 정적분
주기가 $p$인 연속함수 $f(x)$에 대하여
① $\displaystyle \int_{a}^{b} f(x) dx = \int_{a+p}^{b+p} f(x) dx$
② $\displaystyle \int_{a}^{a+p} f(x) dx = \int_{b}^{b+p} f(x) dx$
5. 치환적분법을 이용한 정적분
(1) 치환적분법을 이용한 정적분
함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속이고 미분가능한 함수 $x = g(t)$에 대하여 $a = g(\alpha)$, $b = g(\beta)$일 때 도함수 $g^{\prime}(t)$가 $\alpha$, $\beta$를 포함하는 구간에서 연속이면 $$\int_{a}^{b}f(x) dx = \int_{\alpha}^{\beta}f(g(t))g^{\prime}(t) dt$$
(2) 삼각함수를 이용한 치환적분법
① 피적분함수가 $\sqrt{a^{2} -\,x^{2}}$ ($a$는 상수) 꼴이면 $x = a \sin \theta\:\left( -\dfrac{\pi}{2} \le \theta \le \dfrac{\pi}{2} \right)$로 치환하고 적분합니다.
② 피적분함수가 $\dfrac{1}{x^{2} + a^{2}}$ ($a$는 상수) 꼴이면 $x = a \tan \theta\:\left( -\dfrac{\pi}{2} \lt \theta \lt \dfrac{\pi}{2} \right)$로 치환하고 적분합니다.
6. 부분적분법을 이용한 정적분
닫힌구간 $[\,a, \,b\,]$에서 두 함수 $f(x)$, $g(x)$가 미분가능하고 $f^{\prime}(x)$, $g^{\prime}(x)$가 연속일 때, $$\int_{a}^{b}f(x)g^{\prime}(x)dx = \bigg[ f(x)g(x)\bigg]_{a}^{b} -\,\int_{a}^{b}f^{\prime}(x)g(x)dx$$
7. 정적분으로 정의된 함수
(1) 정적분으로 정의된 함수의 미분
① $\displaystyle \frac{d}{dx} \int_{a}^{x} f(t) dt = f(x)$ (단, $a$는 실수)
② $\displaystyle \frac{d}{dx} \int_{x}^{x+a} f(t) dt = f(x+a) -\, f(x)$ (단, $a$는 실수)
(2) 정적분으로 정의된 함수의 극한
① $\displaystyle \lim_{x \to 0}\frac{1}{x} \int_{a}^{x+a} f(t) dt = f(a)$
② $\displaystyle \lim_{x \to 0}\frac{1}{x -a} \int_{a}^{x} f(t) dt = f(a)$
8. 정적분과 급수의 합 사이의 관계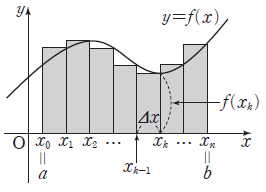
(1) 함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, $$\lim_{n \to \infty}\sum_{k = 1}^{n}f(x_{k})\Delta x = \int_{a}^{b}f(x) dx$$ $$\bigg( \textbf{단, } \Delta x = \frac{b -\,a}{n},\: x_{k} = a + k \Delta x\bigg)$$
(2) 다음과 같이 여러 가지 급수를 정적분으로 나타낼 수 있습니다.
① $\displaystyle \lim_{n \to \infty} \sum_{k=1}^{n}f\bigg( \frac{k}{n}\bigg)\cdot\frac{1}{n} = \int_{0}^{1}f(x) dx$
② $\displaystyle \lim_{n \to \infty} \sum_{k=1}^{n}f\bigg( \frac{p}{n}k\bigg)\cdot\frac{p}{n} = \int_{0}^{p}f(x) dx$
③ $\displaystyle \lim_{n \to \infty} \sum_{k=1}^{n}f\bigg( a + \frac{b -\,a}{n}k\bigg)\cdot\frac{b -\,a}{n} = \int_{a}^{b}f(x) dx$
④ $\displaystyle \lim_{n \to \infty} \sum_{k=1}^{n}f\bigg( a + \frac{p}{n}k\bigg)\cdot\frac{p}{n} = \int_{a}^{a+p}f(x) dx = \int_{0}^{p}f(x + a) dx$
넓이
1. 곡선과 좌표축 사이의 넓이
(1) 함수 $f(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 곡선 $y = f(x)$와 $x$축 및 두 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{a}^{b}|\,f(x)\,| dx$$
(2) 함수 $g(y)$가 닫힌구간 $[\,c, \,d\,]$에서 연속일 때, 곡선 $x = g(y)$와 $y$축 및 두 직선 $y = c$, $y = d$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{c}^{d}|\,g(y)\,| dy$$
2. 두 곡선 사이의 넓이
(1) 함수 $f(x)$, $g(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 두 곡선 $y = f(x)$, $y = g(x)$ 및 두 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{a}^{b}|\,f(x) -\,g(x)\,| dx$$
(2) 함수 $f(y)$, $g(y)$가 닫힌구간 $[\,c, \,d\,]$에서 연속일 때, 두 곡선 $x = f(y)$, $x = g(y)$ 및 두 직선 $y = c$, $y = d$로 둘러싸인 도형의 넓이 $S$는 $$S = \int_{c}^{d}|\,f(y) -\,g(y)\,| dy$$
부피
1. 입체도형의 부피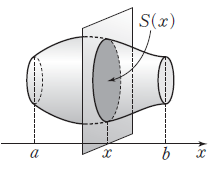
닫힌구간 $[\,a, \,b\,]$에서 $x$좌표가 $x$인 점을 지나고 $x$축에 수직인 평면으로 자른 단면의 넓이가 $S(x)$이고, 함수 $S(x)$가 닫힌구간 $[\,a, \,b\,]$에서 연속일 때, 이 입체도형의 부피 $V$는 $$V = \int_{a}^{b}S(x) dx$$
속도와 거리
1. 속도와 거리
(1) 직선 위를 움직이는 점의 위치와 움직인 거리
수직선 위를 움직이는 점 $\mathrm{P}$의 시각 $t$에서의 속도가 $v(t)$, 시각 $t = a$에서의 위치가 $x_{0}$일 때
① 시각 $t$에서의 점 $\mathrm{P}$의 위치 $x$는 $x = x_{0} + \int_{a}^{b}v(t) dt$
② 시각 $t = a$에서 $t = b$까지 점 $\mathrm{P}$의 위치의 변화량은 $\int_{a}^{b}v(t) dt$
③ 시각 $t = a$에서 $t = b$까지 점 $\mathrm{P}$가 움직인 거리 $s$는 $s = \int_{a}^{b}|\,v(t)\,|dt$
(2) 좌표평면 위를 움직이는 점의 움직인 거리
좌표평면 위를 움직이는 점 $\mathrm{P}$의 시각 $t$에서의 위치 $(x, \,y)$가 $x = f(t)$, $y = g(t)$일 때, 시각 $t = a$에서 $t = b$까지 점 $\mathrm{P}$가 움직인 거리 $s$는 $$s = \int_{a}^{b}\sqrt{\bigg( \dfrac{dx}{dt}\bigg)^{2} + \bigg(\dfrac{dy}{dt}\bigg)^{2} } dt = \int_{a}^{b}\sqrt{\{ f^{\prime}(t)\}^{2} + \{ g^{\prime}(t)\}^{2} } \,dt$$
2. 곡선의 길이
(1) 곡선 $x = f(t)$, $y = g(t)$ ($a \le t \le b$)의 겹치는 부분이 없을 때 길이 $l$은 $$l = \int_{a}^{b}\sqrt{\bigg( \dfrac{dx}{dt}\bigg)^{2} + \bigg(\dfrac{dy}{dt}\bigg)^{2} } dt = \int_{a}^{b}\sqrt{\{ f^{\prime}(t)\}^{2} + \{ g^{\prime}(t)\}^{2} } \,dt$$
(2) 곡선 $y = f(x)$ ($a \le x \le b$)의 길이 $l$은 $$l = \int_{a}^{b}\sqrt{1 + \{ f^{\prime}(x)\}^{2} } \,dx$$