지수함수와 로그함수
람다 $\lambda$의 차례
거듭제곱과 거듭제곱근
1. 거듭제곱근
(1) 거듭제곱
어떤 수 $a$를 여러 번 곱한 $a$, $a^{2}$, $a^{2}$, $a^{3}$, $\cdots\,$을 통틀어 $a$의 거듭제곱이라 하고 $a^{n}$에서 $a$를 거듭제곱의 밑, $n$을 거듭제곱의 지수라고 합니다.
(2) 거듭제곱근
실수 $a$와 $2$ 이상의 자연수 $n$에 대하여 $n$제곱하여 $a$가 되는 수, 즉 방정식 $x^{n} = a$를 만족시키는 $x$를 $a$의 $n$제곱근이라고 합니다. 또 $a$의 제곱근, 세제곱근, 네제곱근, $\cdots\,$을 통틀어 $a$의 거듭제곱근이라고 합니다.
(3) 실수 $a$의 $n$제곱근 중 실수인 것은 다음과 같습니다.
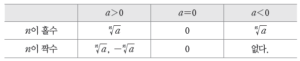
실수 $a$의 $n$제곱근 중 실수인 것은 함수 $y = x^{n}$ ($n \ge 2$인 자연수 $n$)의 그래프와 직선 $y = a$의 교점의 $x$좌표입니다.
① $n$은 홀수 ② $n$은 짝수

(4) $a$의 $n$제곱근 중 실수인 것의 개수를 $h_{n}(a)$라 하면 (단, 중근은 한 개로 세는 경우)
$h_{n}(a) = \begin{cases} \:2 & (n\textbf{은 짝수 그리고 }a \gt 0) \\ \:1 & (n\textbf{은 홀수 또는 }a = 0) \\ \:0 & (n\textbf{은 짝수 그리고 }a \lt 0) \end{cases}$
2. 거듭제곱근의 성질
$a \gt 0$, $b \gt 0$이고 $m$, $n$이 $2$ 이상의 자연수일 때
① $\sqrt[n]{a}\sqrt[n]{b} = \sqrt[n]{ab}$
② $\dfrac{\sqrt[n]{a}}{\sqrt[n]{b}} = \sqrt[n]{\dfrac{a}{b}}$
③ $(\sqrt[n]{a})^{m} = \sqrt[n]{a^{m}}$
④ $\sqrt[m]{\sqrt[n]{a}} = \sqrt[mn]{a} = \sqrt[n]{\sqrt[m]{a}}$
⑤ $\sqrt[np]{a^{mp}} = \sqrt[n]{a^{m}}$ (단, $p$는 자연수)
지수의 확장과 지수법칙
1. 자연수인 지수
(1) 자연수인 지수의 정의
$a$는 실수이고 $a^{1} = a$, $a^{n} = a^{n-1} \times a$ ($n$은 $n \ge 2$인 자연수)
(2) 지수가 자연수일 때의 지수법칙
$a$, $b$는 실수이고 $m$, $n$은 자연수
① $a^{m}a^{n} = a^{m + n}$
② $a^{m}\div a^{n} = \begin{cases} \: a^{m – n} & (m \gt n) \\ \:\: 1 & (m = n) \\ \:\dfrac{1}{a^{n – m}} & (m \lt n) \end{cases}$
③ $(a^{m})^{n} = a^{mn}$
④ $(ab)^{n} = a^{n}b^{n}$
2. 정수인 지수
(1) $0$ 또는 음의 정수인 지수의 정의
$a \ne 0$이고 $n$이 자연수일 때
① $a^{0} = 1$
② $a^{-n} = \dfrac{1}{a^{n}}$
(2) 지수가 정수일 때의 지수법칙
$a \ne 0$, $b \ne 0$이고 $m$, $n$은 정수
① $a^{m}a^{n} = a^{m + n}$
② $a^{m}\div a^{n} = a^{m – n}$
③ $(a^{m})^{n} = a^{mn}$
④ $(ab)^{n} = a^{n}b^{n}$
3. 유리수인 지수
(1) 유리수인 지수의 정의
$a \gt 0$이고 $m$은 정수, $n$은 $2$ 이상의 자연수일 때
$a^{\frac{m}{n}} = \sqrt[n]{a^{m}}$ 특히 $a^{\frac{1}{n}} = \sqrt[n]{a}$
(2) 지수가 유리수일 때의 지수법칙
$a \gt 0$, $b \gt 0$이고 $r$, $s$은 유리수
① $a^{r}a^{s} = a^{r + s}$
② $a^{r}\div a^{s} = a^{r – s}$
③ $(a^{r})^{s} = a^{rs}$
④ $(ab)^{r} = a^{r}b^{r}$
4. 실수인 지수
(1) 실수인 지수의 정의
지수가 무리수인 수, 예를 들어 $2^{\pi}$을 살펴보면 $\pi = 3.14159265359\cdots\,$이고 유리수 $3$, $3.1$, $3.14$, $3.141$, $3.1415$, $3.14159$, $3.141592$, $\cdots\,$ 들을 지수로 갖는 $2^{3}$, $2^{3.1}$, $2^{3.14}$, $2^{3.141}$, $2^{3.1415}$, $2^{3.14159}$, $2^{3.141592}$, $\cdots\,$은 일정한 수에 한없이 가까워진다는 사실[극한]이 알려져 있는데 이 일정한 수를 $2^{\pi}$으로 정의합니다. 이와 같은 방법으로 지수가 무리수인 수를 정의할 수 있습니다. 따라서 $a \gt 0$일 때 임의의 실수 $x$에 대하여 $a^{x}$을 정의할 수 있습니다.
(2) 지수가 실수일 때의 지수법칙
$a \gt 0$, $b \gt 0$이고 $x$, $y$은 실수
① $a^{x}a^{y} = a^{x + y}$
② $a^{x}\div a^{y} = a^{x – y}$
③ $(a^{x})^{y} = a^{xy}$
④ $(ab)^{x} = a^{x}b^{x}$
로그의 뜻과 성질
1. 로그
$a \gt 0$, $a \ne 1$일 때 양수 $N$에 대하여 $a^{x} = N$을 만족시키는 실수 $x$를 $\log_{a}N$으로 나타내고, $a$를 밑으로 하는 $N$의 로그라 합니다. 이때 $N$을 $\log_{a}N$의 진수라고 합니다. $$a^{x} = N\, \Longleftrightarrow \,x = \log_{a}N$$
2. 로그의 성질
(1) 로그의 성질
$a \gt 0$, $a \ne 1$, $M \gt 0$, $N \gt 0$일 때
① $\log_{a}1 = 0$, $\log_{a}a = 1$
② $\log_{a}MN = \log_{a}M + \log_{a}N$
③ $\log_{a}\dfrac{M}{N} = \log_{a}M -\, \log_{a}N$
④ $\log_{a}M^{k} = k\log_{a}M$ (단, $k$는 실수)
(2) 로그의 밑의 변환
$a \gt 0$, $a \ne 1$, $b \gt 0$일 때
① $\log_{a}b = \dfrac{\log_{c}b}{\log_{c}a}$ (단, $c \gt 0$, $c \ne 1$)
② $\log_{a}b = \dfrac{1}{\log_{b}a}$ (단, $b \ne 1$)
(3) 로그의 여러 가지 성질
$a \gt 0$, $a \ne 1$, $b \gt 0$일 때
① $\log_{a^{r}}b^{s} = \frac{s}{r}\log_{a}b$ (단, $r$, $s$는 실수, $r \ne 0$)
② $a^{k \log_{c}b} = b^{k \log_{c}a}$ (단, $c \gt 0$, $c \ne 1$, $k$는 실수)
상용로그
1. 상용로그
(1) 상용로그
$10$을 밑으로 하는 로그를 상용로그라 하고 상용로그 $\log_{10}N$은 보통 밑 $10$을 생략하여 $\log N$과 같이 나타냅니다.
(2) 상용로그표
$0.01$의 간격으로 $1.00$에서 $9.99$까지의 수에 대한 상용로그의 값을 반올림하여 소수점 아래 넷째 자리까지 나타낸 표입니다.
(3) 상용로그의 표현
양수 $N$의 상용로그는 $\log N = n + \alpha$ ($n$은 정수, $0 \le \alpha \lt 1$)와 같이 나타낼 수 있습니다. 이때 $n$은 $\log N$의 정수 부분, $\alpha$는 $\log N$의 소수 부분입니다.
2. 상용로그의 성질
(1) 상용로그의 정수 부분
양수 $N$에 대하여 $\log N = n + \alpha$ ($n$은 정수, $0 \le \alpha \lt 1$)일 때
① $n \ge 0$이면 $N \ge 1$이고 $N$은 정수 부분이 $n + 1$ 자리인 수입니다.
② $n \lt 0$이면 $N \lt 1$이고 $N$은 소수점 아래 $|\,n\,|$째 자리에서 처음으로 $0$이 아닌 숫자가 나타나는 수입니다.
(2) 상용로그의 소수 부분
숫자의 배열이 같고 소수점의 위치만 다른 양수의 상용로그의 소수 부분은 모두 같습니다.
예를 들어 $\log 0.0314$, $\log 3.14$, $\log 31400$의 정수 부분은 각각 $-2$, $0$, $4$이지만 소수 부분은 $\log 3.14$로 모두 같습니다.
지수함수의 뜻과 그래프
1. 지수함수
$a$가 $1$이 아닌 양수일 때, $y = a^{x}$를 $a$를 밑으로 하는 지수함수라고 합니다.
2. 지수함수 $y = a^{x}$의 성질
① 정의역은 실수 전체의 집합이고 치역은 양의 실수 전체의 집합입니다.
② $a \gt 1$일 때, $x$의 값이 증가하면 $y$의 값도 증가합니다.
$0 \lt a \lt 1$일 때, $x$의 값이 증가하면 $y$의 값은 감소합니다.
③ 그래프는 점 $(0, \,1)$을 지나고 점근선은 $x$축입니다.
④ 일대일함수입니다.
공역이 양의 실수 전체의 집합이라면 일대일대응이고 역함수가 존재합니다.
$a \gt 1$일 때 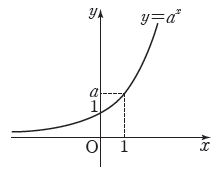
$0 \lt a \lt 1$일 때 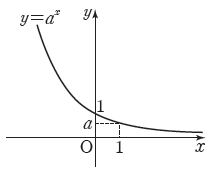
3. 지수함수의 그래프의 평행이동과 대칭이동
지수함수 $y = a^{x}$ ($a \gt 0$, $a \ne 1$)의 그래프를 평행이동 또는 대칭이동한 그래프의 식은 다음과 같습니다.
① $x$축의 방향으로 $m$만큼, $y$축의 방향으로 $n$만큼 평행이동: $y = a^{x -\, m} + n$
② $x$축에 대하여 대칭이동: $y = -\,a^{x}$
③ $y$축에 대하여 대칭이동: $y = a^{-x}$ 즉, $y = \left(\dfrac{1}{a} \right)^{x}$
④ 원점에 대하여 대칭이동: $y = – \left(\dfrac{1}{a} \right)^{x}$
4. 지수함수의 최대, 최소
(1) 정의역이 $\{\,x\,|\,m \le x \le n \, \}$인 지수함수 $y = a^{x}$에 대하여
① $a \gt 1$이면 $x = m$일 때 최솟값 $a^{m}$, $x = n$일 때 최댓값 $a^{n}$을 갖습니다.
② $0 \lt a \lt 1$이면 $x = m$일 때 최댓값 $a^{m}$, $x = n$일 때 최솟값 $a^{n}$을 갖습니다.
(2) 함수 $y = a^{f(x)}$은
① $a \gt 1$이면 $f(x)$가 최대일 때 최댓값, $f(x)$가 최소일 때 최솟값을 갖습니다.
② $0 \lt a \lt 1$이면 $f(x)$가 최대일 때 최솟값, $f(x)$가 최소일 때 최댓값을 갖습니다.
로그함수의 뜻과 그래프
1. 로그함수
지수함수 $y = a^{x}$ ($a \gt 0$, $a \ne 1$)의 역함수 $y = \log_{a}x$를 $a$를 밑으로 하는 로그함수라고 합니다.
2. 로그함수 $y = \log_{a}x$의 성질
① 정의역이 양의 실수 전체의 집합이고, 치역은 실수 전체의 집합입니다.
② $a \gt 1$일 때 $x$의 값이 증가하면 $y$의 값도 증가합니다.
$0 \lt a \lt 1$일 때 $x$의 값이 증가하면 $y$의 값은 감소합니다.
③ 그래프는 점 $(1, \,0)$을 지나고 점근선은 $y$축입니다.
④ 일대일함수입니다. 일대일대응이므로 역함수가 존재합니다.
⑤ 그래프는 지수함수 $y = a^{x}$의 그래프와 직선 $y = x$에 대하여 대칭입니다.
$a \gt 1$일 때 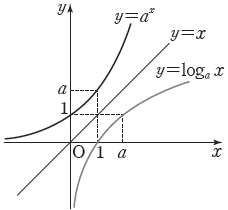
$0 \lt a \lt 1$일 때 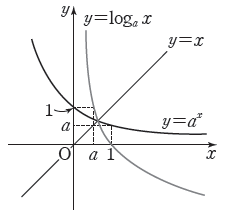
3. 로그함수의 그래프의 평행이동과 대칭이동
로그함수 $y = \log{a}x$ ($a \gt 0$, $a \ne 1$)의 그래프를 평행이동 또는 대칭이동한 그래프의 식은 다음과 같습니다.
① $x$축의 방향으로 $m$만큼, $y$축의 방향으로 $n$만큼 평행이동: $y = \log{a}(x -\, m) + n$
② $x$축에 대하여 대칭이동: $y = – \log{a}x$
③ $y$축에 대하여 대칭이동: $y = \log{a}(-x)$
④ 원점에 대하여 대칭이동: $y = – \log{a}(-x)$
⑤ 직선 $y = x$에 대하여 대칭이동: $y = a^{x}$
4. 로그함수의 최대, 최소
(1) 정의역이 $\{\,x\,|\,0 \lt m \le x \le n \, \}$인 로그함수 $y = \log_{a}x$에 대하여
① $a \gt 1$이면 $x = m$일 때 최솟값 $\log_{a}m$, $x = n$일 때 최댓값 $\log_{a}n$을 갖습니다.
② $0 \lt a \lt 1$이면 $x = m$일 때 최댓값 $\log_{a}m$, $x = n$일 때 최솟값 $y\log_{a}n$을 갖습니다.
(2) 함수 $y = \log_{a}f(x)$ ($f(x) \gt 0$)은
① $a \gt 1$이면 $f(x)$가 최대일 때 최댓값, $f(x)$가 최소일 때 최솟값을 갖습니다.
② $0 \lt a \lt 1$이면 $f(x)$가 최대일 때 최솟값, $f(x)$가 최소일 때 최댓값을 갖습니다.
지수함수와 로그힘수의 활용
1. 지수방정식
(1) 밑을 같게 할 수 있는 경우
주어진 방정식을 $a^{f(x)} = a^{g(x)}$ 꼴로 변형한 후 $$a^{f(x)} = a^{g(x)} \,\Longleftrightarrow \,f(x) = g(x)$$ 임을 이용하여 방정식 $f(x) = g(x)$을 풉니다.
(2) $a^{x}$ 꼴이 반복되는 경우
$a^{x} = t$로 치환하여 $t$에 대한 방정식을 풀고 치환관계를 이용하여 $x$의 값을 구합니다. 이때 $a^{x} \gt 0$이므로 $t \gt 0$임에 주의합니다.
(3) 지수가 같은 경우
$\{ g(x) \}^{f(x)} = \{ h(x) \}^{f(x)}$ 꼴이면 $g(x) = h(x)$ 또는 $f(x) = 0$을 풉니다. (단, $g(x) \gt 0$, $h(x) \gt 0$)
2. 지수부등식
(1) 밑을 같게 할 수 있는 경우
주어진 부등식을 $a^{f(x)} \gt a^{g(x)}$ 꼴로 변형 후
① $a \gt 1$일 때, 부등식 $f(x) \gt g(x)$를 풉니다.
② $0 \lt a \lt 1$일 때, 부등식 $f(x) \lt g(x)$를 풉니다.
(2) $a^{x}$ 꼴이 반복되는 경우
$a^{x} = t$로 치환하여 $t$에 대한 부등식을 풀고 치환관계를 이용하여 $x$ 값의 범위를 구합니다. 이때 $a^{x} \gt 0$이므로 $t \gt 0$임에 주의합니다.
3. 로그방정식
(1) $\log_{a}f(x) = b$ 꼴인 경우
다음을 이용하여 풉니다. (단, $a \gt 0$, $a \ne 1$) $$\log_{a}f(x) = b \,\Longleftrightarrow \,f(x) = a^{b}$$
(2) 밑을 같게 할 수 있는 경우
주어진 방정식을 $\log_{a}f(x) = \log_{a}g(x)$ 꼴로 변형한 후 $$\log_{a}f(x) = \log_{a}g(x) \,\Longleftrightarrow \,f(x) = g(x)$$임을 이용하여 방정식 $f(x) = g(x)$를 풉니다. (단, $a \gt 0$, $a \ne 1$, $f(x) \gt 0$, $g(x) \gt 0$)
(3) $\log_{a}x$ 꼴이 반복되는 경우
$\log_{a}x = t$로 치환하여 $t$에 대한 방정식을 풀고 치환관계를 이용하여 $x$의 값을 구합니다.
(4) 진수가 같은 경우
$\log_{g(x)}f(x) = \log_{h(x)}f(x)$ 꼴이면 $g(x) = h(x)$ 또는 $f(x) = 1$을 풉니다. (단, $f(x) \gt 0$, $g(x) \gt 0$, $g(x) \ne 1$, $h(x) \gt 0$, $h(x) \ne 1$)
(5) 지수에 로그가 있는 경우
양변에 로그를 취하여 풉니다.
4. 로그부등식
(1) 밑을 같게 할 수 있는 경우
주어진 부등식을 $\log_{a}f(x) \gt \log_{a}g(x)$ 꼴로 변형한 후
① $a \gt 1$일 때, 부등식 $f(x) \gt g(x) \gt 0$을 풉니다.
② $0 \lt a \lt 1$일 때, 부등식 $0 \lt f(x) \lt g(x)$을 풉니다.
(2) $\log_{a}x$ 꼴이 반복되는 경우
$\log_{a}x = t$로 치환하여 $t$에 대한 부등식을 풀고 치환관계를 이용하여 $x$ 값의 범위를 구합니다.
(3) 지수에 로그가 있는 경우
양변에 로그를 취하여 풉니다. 이때 로그의 밑이 $0$과 $1$ 사이면 부등호의 방향이 바뀐다는 것에 주의합니다.
