통계
람다 $\lambda$의 차례
확률변수와 확률분포
1. 확률변수
어떤 시행에서 표본공간 $S$의 각 원소에 단 하나의 실수가 대응되는 함수를 확률변수라 하고 확률변수 $X$가 어떤 값 $x$를 가질 확률을 기호로 $\mathrm{P}(X = x)$와 같이 나타냅니다.
2. 확률분포
확률변수 $X$가 갖는 값과 $X$가 이 값을 가질 확률의 대응 관계를 확률변수 $X$의 확률분포라고 합니다.
이산확률변수의 기댓값과 표준편차
1. 이산확률변수
(1) 이산확률변수
확률변수가 가질 수 있는 값들이 유한개이거나 자연수와 같이 셀 수 있을 때, 이 확률변수를 이산확률변수라 합니다.
(2) 확률질량함수
이산확률변수 $X$가 가질 수 있는 모든 값 $x_1$, $x_2$, $\cdots$, $x_n$에 이 값을 가질 확률 $p_1$, $p_2$, $\cdots$, $p_n$이 대응되는 관계를 나타내는 함수 $$\mathrm{P}(X = x_{i}) = p_{i}\:\,(i = 1, 2, \cdots, n)$$를 이산확률변수 $X$의 확률질량함수라 합니다.
(3) 확률질량함수의 성질
이산확률변수 $X$의 확률질량함수 $\mathrm{P}(X = x_{i}) = p_{i}\:\,(i = 1, 2, \cdots, n)$에 대하여
① $0 \le p_{i} \le 1$
② $p_{1} + p_{2} + \cdots + p_{n} = 1$
③ $\mathrm{P}(x_{i} \le X \le x_{j}) = p_{i} + p_{i+1} + \cdots + p_{j}$
(단, $j = 1, 2, \cdots, n$, $\,i \le j\,$)
2. 이산확률변수의 기댓값(평균), 분산, 표준편차
이산확률변수 $X$의 확률질량함수가 $\mathrm{P}(X = x_{i}) = p_{i}$ ($i = 1, 2, \cdots, n$)일 때
① 기댓값(평균): $\mathrm{E}(X) = x_{1}p_{1} + x_{2}p_{2} + \cdots + x_{n}p_{n}$
② 분산: $\mathrm{V}(X)$
$= \mathrm{E}(\,(X-\,m)^{2}) = (x_{1} -\,m)^{2}p_{1} + (x_{2} -\,m)^{2}p_{2} + \cdots + (x_{n} -\,m)^{2}p_{n}$
$= \mathrm{E}(X^{2}) – \,m^{2}$ (단, $m = \mathrm{E}(X)\,$)
③ 표준편차: $\sigma(X) = \sqrt{\mathrm{V}(X)}$
3. 확률변수 $aX + b$의 평균, 분산, 표준편차
확률변수 $X$와 두 상수 $a$, $b$ ($a \ne 0$)에 대하여
① $\mathrm{E}(aX + b) = a\mathrm{E}(X) + b$
② $\mathrm{V}(aX + b) = a^{2}\mathrm{V}(X)$
③ $\sigma(aX + b) = |\,a\,|\sigma(X)$
이항분포
1. 이항분포
(1) 이항분포
한 번의 시행에서 사건 $A$가 일어날 확률이 $p$로 일정할 때, $n$번의 독립시행에서 사건 $A$가 일어나는 횟수를 확률변수 $X$라 하면 $X$가 가질 수 있는 값은 $0$, $1$, $2$, $\cdots$, $n$이고, $X$의 확률질량함수는 다음과 같습니다. $$\mathrm{P}(X = r) = {}_{n}\mathrm{C}_{r}p^{r}q^{n-\,r}\:\,(r = 0, 1, 2, \cdots, n,\,q = 1-\,p)$$이과 같은 확률분포를 이항분포라 호고, 기호로 $\mathrm{B}(n, p)$와 같이 나타냅니다. 이때 확률변수 $X$는 이항분포 $\mathrm{B}(n, p)$를 따른다고 합니다.
(2) 이항분포에서의 평균, 분산, 표준편차
확률변수 $X$는 이항분포 $\mathrm{B}(n, p)$를 따를 때 (단, $q = 1 -\,p\,$) $$\mathrm{E}(X) = np,\:\mathrm{V}(X) = npq,\:\sigma(X) = \sqrt{npq}$$
2. 큰수의 법칙
어떤 시행에서 사건 $A$가 일어날 수학적 확률이 $p$이고, $n$번의 독립시행에서 사건 $A$가 일어나는 횟수를 $X$라 할 때, 충분히 작은 양수 $h$에 대하여 $n$의 값이 한없이 커질수록 확률 $\mathrm{P}\left( \left| \dfrac{X}{n} -\,p\, \right| \lt h \right)$는 $1$에 가까워집니다. 이것을 큰수의 법칙이라고 합니다.
정규분포
1. 연속확률변수
(1) 연속확률변수
확률변수가 어떤 범위에 속하는 모든 실수의 값을 가질 때, 이 확률변수를 연속확률변수라 합니다.
(2) 확률밀도함수
$\alpha \le X \le \beta$에서 모든 실수의 값을 가지는 연속확률변수 $X$에 대하여 $\alpha \le x \le \beta$에서 정의된 함수 $f(x)$가 다음 세 가지 성질을 모두 만족시킬 때, 함수 $f(x)$를 확률변수 $X$의 확률밀도함수라고 합니다.
① $f(x) \ge 0$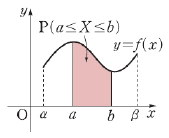
② $y = f(x)$의 그래프와 $x$축 및 두 직선 $x = \alpha$, $x = \beta$로 둘러싸인 도형의 넓이는 $1$이다.
③ $\mathrm{P}(a \le X \le b)$는 $y = f(x)$의 그래프와 $x$축 및 두 직선 $x = a$, $x = b$로 둘러싸인 도형의 넓이와 같다. (단, $\alpha \le a \le b \le \beta\,$)
2. 정규분포
(1) 정규분포
실수 전체의 집합에서 정의된 연속확률변수 $X$의 확률밀도함수 $f(x)$가 두 상수 $m$, $\sigma$ ($\sigma \gt 0$)에 대하여 $f(x) = \dfrac{1}{\sqrt{2\pi}\sigma}e^{- \frac{(x -\,m)^{2}}{2 \sigma^{2}}}$일 때, $X$의 확률분포를 정규분포라 합니다.
이때 확률밀도함수 $f(x)$의 그래프는 오른쪽 그림과 같고 이 곡선을 정규분포곡선이라 합니다. 또 확률변수 $X$의 평균은 $m$, 표준편차는 $\sigma$임이 알려져 있습니다.
평균이 $m$, 표준편차가 $\sigma$인 정규분포를 기호로 $\mathrm{N}(m, \sigma^{2})$와 같이 나타내고 확률변수 $X$는 정규분포 $\mathrm{N}(m, \sigma^{2})$를 따른다고 합니다.
(2) 정규분포곡선의 성질
정규분포 $\mathrm{N}(m, \sigma^{2})$을 따르는 확률변수 $X$의 정규분포곡선은 다음과 같은 성질을 갖습니다.
① 직선 $x = m$에 대하여 대칭이고 $x$축이 점근서이 종 모양의 곡선이다.
② 곡선과 $x$축 사이의 넓이는 $1$이다.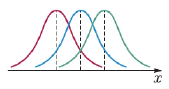
③ $\sigma$의 값이 일정할 때, $m$의 값이 달라지면 대칭축의 위치는 바뀌지만 곡선의 모양은 변하지 않는다.
④ $m$의 값이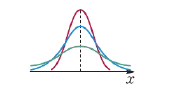
일정할 때, $\sigma$의 값이 클수록 가운데 부분의 높이는 낮아지고 옆으로 퍼진 모양이다.
3. 표준정규분포
평균이 $0$이고 분산이 $1$인 정규분포 $\mathrm{N}(0, 1)$을 표준정규분포라고 합니다.
확률변수 $Z$가 표준정규분포 $\mathrm{N}(0, 1)$을 따를 때, $Z$의 확률밀도함수는 $f(x) = \dfrac{1}{\sqrt{2\pi}}e^{-\frac{x^2}{2}}$이고 그 그래프는 오른쪽 그림과 같습니다.
또 양수 $z$에 대하여 확률 $\mathrm{P}(0 \le Z \le z)$는 그림에서 색칠한 부분의 넓이와 같고, 그 값은 표준정규분포표에서 찾을 수 있습니다.
4. 정규분포의 표준화
확률변수 $X$가 정규분포 $\mathrm{N}(m, \sigma^{2})$을 따를 때, 확률변수 $Z = \dfrac{X -\,m}{\sigma}$은 표준정규분포 $\mathrm{N}(0, 1)$을 따릅니다.
정규분포 $\mathrm{N}(m, \sigma^{2})$을 따르는 확률변수 $X$를 표준정규분포 $\mathrm{N}(0, 1)$을 따르는 확률변수 $Z = \dfrac{X -\,m}{\sigma}$으로 바꾸는 것을 표준화한다고 합니다.
5. 이항분포와 정규분포의 관계
확률변수 $X$가 이항분포 $\mathrm{B}(n, p)$를 따를 때, $n$이 충분히 크면 $X$는 근사적으로 정규분포 $\mathrm{N}(np, npq)$를 따릅니다. (단, $q = 1 -\,p\,$)
모집단과 표본
1. 모집단과 표본
(1) 모집단과 전수조사
① 통계조사에서 조사하고자 하는 대상 전체를 모집단이라 합니다.
② 모집단 전체를 조사하는 것을 전수조사라 합니다.
(2) 표본과 표본조사
① 모집단에서 뽑은 일부분을 표본이라 합니다.
② 표본을 뽑아 조사하는 것을 표본조사라 합니다.
③ 표본조사에서 뽑은 표본의 개수를 표본의 크기라고 합니다.
(3) 임의추출
모집답에 속하는 각 대항이 같은 확률로 추출되도록 표본을 추출하는 방법을 임의추출이라 합니다.
① 한 개의 자료를 뽑은 후 되돌려 놓고 다시 뽑는 방법을 복원추출이라 합니다.
② 한 개의 자료를 뽑은 후 되돌려 놓지 않고 뽑는 방법을 비복원추출이라 합니다.
2. 모평균과 표본평균
(1) 모집단에서 조사하고자 하는 특성을 나타내는 확률변수를 $X$라 할 때, $X$의 평균, 분산, 표준편차를 각각 모평균, 모분산, 모표준편차라 하고 기호로 각각 $m$, $\sigma^{2}$, $\sigma$와 같이 나타냅니다.
(2) 모집단에서 임의추출한 크기가 $n$인 표본을 $X_1$, $X_2$, $\cdots$, $X_n$라 할 때, 표본평균, 표본분산, 표본표준편차를 각각 기호로 $\overline{X}$, $S^{2}$, $S$와 같이 나타내고 다음과 같이 정의합니다.
$\overline{X} = \dfrac{1}{n}\left( X_{1} + X_{2} + \cdots + X_{n} \right)$
$S^{2} = \dfrac{1}{n -\,1}\left( (X -\,X_{1})^{2} + (X -\,X_{2})^{2} + \cdots + (X -\,X_{n})^{2} \right)$
$S = \sqrt{S^{2}}$
위에서 모평균 $m$은 고정된 상수이지만 표본평균 $\overline{X}$는 추출된 표본에 따라 여러 가지 값을 가질 수 있는 확률변수입니다.
3. 표본평균의 평균, 분산, 표준편차
모평균이 $m$이고 모표준편차가 $\sigma$인 모집단에서 임의추출한 크기가 $n$인 표본의 표본평균 $\overline{X}$에 대하여 $$\mathrm{E}(\overline{X}) = m,\:\, \mathrm{V}(\overline{X}) = \frac{\sigma^{2}}{n},\:\, \mathrm{\sigma}(\overline{X}) = \frac{\sigma}{\sqrt{n}}$$
모평균의 추정
1. 표본평균의 분포
모평균이 $m$, 모표준편차가 $\sigma$인 모집단에서 임의추출한 크기가 $n$인 표본의 표본평균 $\overline{X}$에 대하여 다음이 성립합니다.
① 모집단이 정규분포를 따르면 $n$의 크기에 관계없이 표본평균 $\overline{X}$는 정규분포 $\mathrm{N}\left(m,\, \dfrac{\sigma^{2}}{n} \right)$을 따릅니다.
② 모집단이 정규분포를 따르지 않아도 $n$이 충분히 크면 표본평균 $\overline{X}$는 근사적으로 정규분포 $\mathrm{N}\left(m,\, \dfrac{\sigma^{2}}{n} \right)$을 따릅니다.
2. 모평균의 추정
(1) 표본을 조사해 얻은 정보를 이용하여 모평균, 모표준편차와 같이 모집단의 특성을 나타내는 값을 추측하는 것을 추정이라 합니다.
(2) 모평균에 대한 신뢰구간
정규분포 $\mathrm{N}(m, \sigma^{2})$을 따르는 모집단에서 임의추출한 크기가 $n$인 표본의 표본평균 $\overline{X}$의 값이 $\overline{x}$일 때, 신뢰도에 따른 모평균 $m$에 대한 신뢰구간은 다음과 같습니다.
① 신뢰도 $95$%의 신뢰구간: $\overline{x} -\,1.96\dfrac{\sigma}{\sqrt{n}} \le m \le \overline{x} + 1.96\dfrac{\sigma}{\sqrt{n}}$
② 신뢰도 $99$%의 신뢰구간: $\overline{x} -\,2.58\dfrac{\sigma}{\sqrt{n}} \le m \le \overline{x} + 2.58\dfrac{\sigma}{\sqrt{n}}$
③ 모평균 $m$에 대한 신뢰구간이 $\overline{x} -\,k\dfrac{\sigma}{\sqrt{n}} \le m \le \overline{x} + k\dfrac{\sigma}{\sqrt{n}}$일 때 신뢰구간의 길이는 $2k\dfrac{\sigma}{\sqrt{n}}$입니다.
모비율의 추정
1. 표본비율의 평균, 분산, 표준편차
크기가 $n$인 표본에서 어떤 사건이 일어난 횟수를 확률변수 $X$라 할 때 그 사건에 대한 표본비율 $\hat{p}$은 $\hat{p} = \dfrac{X}{n}$이고 모비율이 $p$이고, 표본의 크기가 $n$일 때, 표본비율 $\hat{p}$의 평균, 분산, 표준편차는 다음과 같습니다. (단, $q = 1 -\,p\,$) $$\mathrm{E}(\hat{p}) = p,\:\, \mathrm{V}(\hat{p}) = \frac{pq}{n},\:\, \mathrm{\sigma}(\hat{p}) = \sqrt{\frac{pq}{n}}$$
2. 표본비율의 분포
모비율이 $p$이고 표본의 크기 $n$이 충분히 클 때, 표본비율 $\hat{p}$은 근사적으로 정규분포 $\mathrm{N}\left( p, \,\dfrac{pq}{n} \right)$를 따릅니다.
3. 모비율의 추정
모집단에서 크기가 $n$인 표본을 임의추출하여 구한 표본비율을 $\hat{p}$이라 할 때, 표본의 크기 $n$이 충분히 크면 신뢰도에 따른 모비율 $p$의 신뢰구간은 다음과 같습니다. (단, $\hat{q} = 1 -\,\hat{p}\,$)
① 신뢰도 $95$%의 신뢰구간: $\hat{p} -\,1.96\sqrt{\dfrac{\hat{p}\hat{q}}{n}} \le p \le \hat{p} +1.96\sqrt{\dfrac{\hat{p}\hat{q}}{n}}$
② 신뢰도 $99$%의 신뢰구간: $\hat{p} -\,2.58\sqrt{\dfrac{\hat{p}\hat{q}}{n}} \le p \le \hat{p} +2.58\sqrt{\dfrac{\hat{p}\hat{q}}{n}}$
③ 표본의 크기 $n$이 충분히 크면 표본비율 $\hat{p}$의 표준편차 $\sqrt{\dfrac{pq}{n}}$에서 모비율 $p$ 대신 표본비율 $\hat{p}$을 이용한 $Z = \dfrac{\hat{p} -\,p}{\sqrt{\dfrac{\hat{p}\hat{q}}{n}}}$는 근사적으로 표준정규분포 $\mathrm{N}(0, 1)$을 따른다는 것이 알려져 있습니다.