25년 6월 평가원
3. 수열 $\{ a_n \}$에 대하여 $\displaystyle \sum_{k = 1}^{7}a_{k} = 8$일 때, $\displaystyle \sum_{k = 1}^{7}(2a_{k} + 1)$의 값은? [3점]
① $21$
② $22$
③ $23$
④ $24$
⑤ $25$
4. 함수 $$f(x) = \begin{cases} -x^{2} + a & (x \lt 3) \\ \\ \:\, 5x - a & (x \ge 3) \end{cases}$$ 이 실수 전체의 집합에서 연속일 때, 상수 $a$의 값은? [3점]
① $10$
② $11$
③ $12$
④ $13$
⑤ $14$
③
함수 $y = -x^{2} + a$와 함수 $y = 5x -\,a$는 실수 전체의 집합에서 연속이므로 함수 $f(x)$가 $x = 3$에서 연속이면 실수 전체의 집합에서 연속이다.
이때
$\displaystyle \lim_{x \to 3-}f(x) = \lim_{x \to 3-}(-x^{2} + a) = -9 + a$
$\displaystyle \lim_{x \to 3+}f(x) = \lim_{x \to 3-}(5x -\,a) = 15 -\,a$
$f(3) = 15 -\,a$
이므로
$\displaystyle \lim_{x \to 3-}f(x) = \lim_{x \to 3+}f(x) = f(3)$
에서
$-9 + a = 15 -\,a$
따라서 $a = 12$
6. 두 양수 $a$, $b$에 대하여 함수 $f(x) = a \cos bx + 1$ 의 최댓값이 $8$이고 주기가 $\pi$일 때, $a + b$의 값은? [3점]
① $\frac{15}{2}$
② $8$
③ $\frac{17}{2}$
④ $9$
⑤ $\frac{19}{2}$
8. $\sin (\pi -\,\theta) \gt 0$이고 $2 \cos \theta = \sin \theta$일 때, $\cos \theta$의 값은? [3점]
① $-\frac{\sqrt{5}}{5}$
② $-\frac{\sqrt{5}}{10}$
③ $0$
④ $\frac{\sqrt{5}}{10}$
⑤ $\frac{\sqrt{5}}{5}$
⑤
$\sin (\pi -\,\theta) \gt 0$에서 $\sin\theta \gt 0$
$2 \cos \theta = \sin \theta$ $\cdots\cdots$ ㉠
㉠에서 $\sin\theta \gt 0$이므로 $\cos\theta \gt 0$
㉠의 양변을 제곱하면 $4 \cos^{2} \theta = \sin^{2} \theta$
$\sin^{2} \theta = 1 -\,\cos^{2} \theta$이므로 이를 위 등식에 대입하면
$4 \cos^{2} \theta = 1 -\,\cos^{2} \theta$
$5\cos^{2} \theta = 1$
$\cos^{2} \theta = \frac{1}{5}$
따라서 $\cos\theta \gt 0$이므로
$\cos\theta = \dfrac{\sqrt{5}}{5}$
9. 함수 $f(x) = x^{2} + ax$에 대하여 $$\int_{-3}^{3}(x + 1)f(x) dx = 36 + \int_{-3}^{3}f(x) dx$$ 일 때, 상수 $a$의 값은? [4점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
②
$\int_{-3}^{3}(x + 1)f(x) dx = 36 + \int_{-3}^{3}f(x) dx$에서
$\int_{-3}^{3}(x + 1)f(x) dx$
$= \int_{-3}^{3}\{xf(x) + f(x)\} dx$
$= \int_{-3}^{3}xf(x) dx + \int_{-3}^{3}f(x) dx$
이므로
$\int_{-3}^{3}xf(x) dx = 36$
이때 $f(x) = x^{2} + ax$이므로
$\int_{-3}^{3}xf(x) dx = \int_{-3}^{3}x(x^{2} + ax) dx$
$= \int_{-3}^{3}(x^{3} + ax^{2}) dx$
$= 2\int_{0}^{3}ax^{2} dx$
$= 2\bigg[ \dfrac{a}{3}x^{3} \bigg]_{0}^{3} = 2 \times 9a = 18a$
따라서 $18a = 36$이므로 $a = 2$
10. 실수 $a$ ($a \gt 1$)에 대하여 곡선 $y = \log_{a}(x + 3)$이 곡선 $y = \log_{a}(-x + 3)$과 만나는 점을 $\mathrm{A}$, 곡선 $y = \log_{a}(x + 3)$이 $x\,$축과 만나는 점을 $\mathrm{B}$, 곡선 $y = \log_{a}(-x + 3)$이 $x\,$축과 만나는 점을 $\mathrm{C}$라 하자. 삼각형 $\mathrm{ABC}$가 정삼각형일 때, $a$의 값은? [4점]
① $3^{\frac{\sqrt{3}}{6}}$
② $3^{\frac{\sqrt{3}}{4}}$
③ $3^{\frac{\sqrt{3}}{3}}$
④ $3^{\frac{5\sqrt{3}}{12}}$
⑤ $3^{\frac{\sqrt{3}}{2}}$
①
곡선 $y = \log_{a}(x + 3)$이 곡선 $y = \log_{a}(-x + 3)$과 만나는 점 $\mathrm{A}$의 좌표를 구해 보자
$\log_{a}(x + 3) = \log_{a}(-x + 3)$에서 $x + 3 = -x + 3$
$x = 0$
$x = 0$일 때, $y = \log_{a}3$이므로
점 $\mathrm{A}$의 좌표는 $(0, \log_{a}3)$이다.
곡선 $y = \log_{a}(x + 3)$에서 $y = 0$일 때 $\log_{a}(x + 3) = 0$
$x + 3 = 1$, $x = -2$
그러므로 점 $\mathrm{B}$의 좌표는 $(-2, 0)$이다.
곡선 $y = \log_{a}(-x + 3)$에서 $y = 0$일 때
$\log_{a}(-x + 3) = 0$에서 $-x + 3 = 1$
$x = 2$
그러므로 점 $\mathrm{C}$의 좌표는 $(2, 0)$이다.
삼각형 $\mathrm{ABC}$가 정삼각형이므로 원점을 $\mathrm{O}$라 하면
$\tan \dfrac{\pi}{3} = \dfrac{\overline{\mathrm{OA}}}{\overline{\mathrm{OB}}}$에서
$\sqrt{3} = \dfrac{\log_{a}3}{2}$, $\log_{a}3 = 2 \sqrt{3}$
$a^{2\sqrt{3}} = 3$
따라서 $a = 3^{\frac{1}{2\sqrt{3}}} = 3^{\frac{\sqrt{3}}{6}}$
11. 시각 $t = 0$일 때 출발하여 수직선 위를 움직이는 점 $\mathrm{P}$가 있다. 시각이 $t$ ($t \ge 0$)일 때 점 $\mathrm{P}$의 위치 $x$가 $$x = t^{3} - t^{2} - t + 1$$ 이다. <보기>에서 옳은 것만을 있는 대로 고른 것은? [4점]
ㄱ. 시각 $t = 1$일 때 점 $\mathrm{P}$의 위치는 $1$이다.
ㄴ. 시각 $t = 1$일 때 점 $\mathrm{P}$의 속도는 $0$이다.
ㄷ. 출발한 후 점 $\mathrm{P}$의 운동 방향이 바뀌는 시각에 점 $\mathrm{P}$의 가속도는 $4$이다.
① ㄱ
② ㄴ
③ ㄷ
④ ㄱ, ㄷ
⑤ ㄴ, ㄷ
⑤
ㄱ.
$x = t^{3} -\,t^{2} -\,t + 1$에 $t = 1$을 대입하면
$x = 1^{3} -\,1^{2} -\,1 + 1 = 0$ (거짓)
ㄴ.
점 $\mathrm{P}$의 시각 $t$에서의 속도를 $v$라 하면
$v = \frac{dx}{dt} = 3t^{2} -\,2t -\,1$
이므로 시각 $t = 1$일 때 점 $\mathrm{P}$의 속도는
$v = 3 \times 1^{2} -\,2 \times 1 -\,1 = 0$ (참)
ㄷ.
ㄴ에서 시각 $t = 1$일 때 점 $\mathrm{P}$의 속도는 $0$이고 시각 $t = 1$의 좌우에서 속도 $v$의 부호가 음에서 양으로 바뀌므로 출발한 후
점 $\mathrm{P}$의 운동 방향이 바뀌는 시각은 $t = 1$이다. 점 $\mathrm{P}$의 시각 $t$에서의 가속도를 $a$라 하면
$a = \frac{dv}{dt} = 6t -\,2$
이므로 시각 $t = 1$일 때 점 $\mathrm{P}$의 가속도는
$a = 6 \times 1 -\,2 = 4$ (참)
이상에서 옳은 것은 ㄴ, ㄷ이다.
12. 다음 조건을 만족시키는 모든 수열 $\{ a_{n} \}$에 대하여 $a_4$의 최댓값은? [4점]
(가) $a_{1} = a_{3}$
(나) 모든 자연수 $n$에 대하여
$(a_{n+1} -\,a_{n} + 3)(a_{n+1} -\,2a_{n}) = 0$
이다.
① $9$
② $12$
③ $15$
④ $18$
⑤ $21$
②
조건 (나)에서 $a_{n+1} = a_{n} -\,3$ 또는 $a_{n+1} = 2a_{n}$
조건 (가)에서 $a_{3} = a_1$ $\cdots\cdots$ ㉠
(ⅰ) $a_{3} = a_{2} -\,3$, $a_{2} = a_{1} -\,3$인 경우
$a_{3} = a_{2} -\,3 = (a_{1} -\,3) -\,3$
$a_{3} = a_{1} -\,6$
이 식은 ㉠을 만족시키지 않는다.
(ⅱ) $a_{3} = a_{2} -\,3$, $a_{2} = 2a_{1}$인 경우
$a_{3} = a_{2} -\,3 = 2a_{1} -\,3$
㉠에서 $a_{3} = 2a_{3} -\,3$, $a_{3} = 3$
$a_{4} = a_{3} -\,3 = 0$ 또는 $a_{4} = 2a_{3} = 6$
(ⅲ) $a_{3} = 2a_{2}$, $a_{2} = a_{1} -\,3$인 경우
$a_{3} = 2(a_{1} -\,3) = 2a_{1} -\,6$
㉠에서 $a_{3} = 2a_{3} -\,6$, $a_{3} = 6$
$a_{4} = a_{3} -\,3 = 3$ 또는 $a_{4} = 2a_{3} = 12$
(ⅳ) $a_{3} = 2a_{2}$, $a_{2} = 2a_{1}$인 경우
$a_{3} = 2a_{2} = 2(2a_{1}) = 4a_{1}$
㉠에서 $a_{3} = 4a_{3}$, $a_{3} = 0$
$a_{4} = a_{3} -\,3 = -3$ 또는 $a_{4} = 2a_{3} = 0$
(ⅰ) ~ (ⅳ)에서
$a_{4} = -3$ 또는 $a_{4} = 0$ 또는 $a_{4} = 3$ 또는 $a_{4} = 6$ 또는 $a_{4} = 12$
이므로
$a_{4}$의 최댓값은 $12$
13. 그림과 같이 함수 $f(x) = 3x^{2} - 7x + 2$에 대하여 곡선 $y = f(x)$와 직선 $y = \dfrac{1}{3}x -\,\dfrac{2}{3}$ 및 $y\,$축으로 둘러싸인 영역을 $A$, 곡선 $y = f(x)$와 직선 $y = \dfrac{1}{3}x -\,\dfrac{2}{3}$로 둘러싸인 영역을 $B$, 곡선 $y = f(x)$와 두 직선 $y = \dfrac{1}{3}x -\,\dfrac{2}{3}$, $x = k$ ($k \gt 2$)로 둘러싸인 영역을 $C$라 하자. $$\textbf{(}A\textbf{의 넓이)} + \textbf{(}C\textbf{의 넓이)} = \textbf{(}B\textbf{의 넓이)}$$ 일 때, 상수 $k$의 값은? [4점]
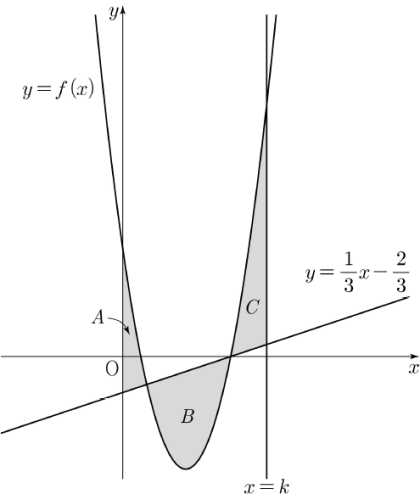
① $\frac{29}{12}$
② $\frac{5}{2}$
③ $\frac{31}{12}$
④ $\frac{8}{3}$
⑤ $\frac{11}{4}$
④
주어진 조건에서
$\textbf{(}A\textbf{의 넓이)} + \textbf{(}C\textbf{의 넓이)} = \textbf{(}B\textbf{의 넓이)}$
가 성립해야 하므로
$\int_{0}^{k}\{ (3x^{2} -\,7x + 2) -\,(\frac{1}{3}x -\,\frac{2}{3}) \} dx = 0$
$\int_{0}^{k}(3x^{2} -\,\frac{22}{3}x + \frac{8}{3}) dx = 0$
$[\,x^{3}-\,\frac{11}{3}x^{2} + \frac{8}{3}x\,]_{0}^{k} = 0$
$k^{3}-\,\frac{11}{3}k^{2} + \frac{8}{3}k = 0$
$3k^{3} -\,11k^{2} + 8k = 0$
$k(k -\,1)(3k -\,8) = 0$
이때 $k \gt 2$이므로 $k = \dfrac{8}{3}$
14. $\overline{\mathrm{AB}} = 2\sqrt{7}$인 삼각형 $\mathrm{ABC}$에서 선분 $\mathrm{BC}$의 중점을 $\mathrm{P}$, 선분 $\mathrm{BC}$를 $5 : 1$로 내분하는 점을 $\mathrm{Q}$라 하자. $$\overline{\mathrm{AQ}} = 3\sqrt{2}, \:\,\sin (\angle \mathrm{QAP}) : \sin (\angle \mathrm{APQ}) = \sqrt{2} : 3$$ 일 때, 삼각형 $\mathrm{ABC}$의 외접원의 넓이는? [4점]
① $\frac{85}{9}\pi$
② $\frac{88}{9}\pi$
③ $\frac{91}{9}\pi$
④ $\frac{94}{9}\pi$
⑤ $\frac{97}{9}\pi$
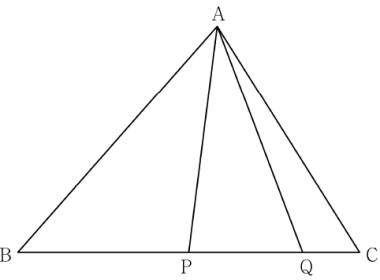
②
삼각형 $\mathrm{APQ}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{PQ}}}{\sin (\angle \mathrm{QAP})} = \dfrac{\overline{\mathrm{AQ}}}{\sin (\angle \mathrm{APQ})}$
조건에서 $\overline{\mathrm{AQ}} = 3\sqrt{2}$이고
$\sin (\angle \mathrm{QAP}) : \sin (\angle \mathrm{APQ}) = \sqrt{2} : 3$이므로
$\overline{\mathrm{PQ}} = \dfrac{\sin (\angle \mathrm{QAP})}{\sin (\angle \mathrm{APQ})} \times \overline{\mathrm{AQ}} = \dfrac{\sqrt{2}}{3} \times 3\sqrt{2} = 2$
점 $\mathrm{P}$는 선분 $\mathrm{BC}$의 중점이고 점 $\mathrm{Q}$는 선분 $\mathrm{BC}$를 $5 : 1$로 내분하는 점이므로
$\overline{\mathrm{BC}} = \overline{\mathrm{BP}} + \overline{\mathrm{PQ}} + \overline{\mathrm{QC}}$
$= \frac{1}{2}\overline{\mathrm{BC}} + 2 + \frac{1}{6}\overline{\mathrm{BC}}$
$= \frac{2}{3}\overline{\mathrm{BC}} + 2$
$\frac{1}{3}\overline{\mathrm{BC}} = 2$, $\overline{\mathrm{BC}} = 6$
한편, $\overline{\mathrm{BQ}} = \frac{5}{6}\overline{\mathrm{BC}} = 5$이고
$\overline{\mathrm{AB}} = 2\sqrt{7}$이므로 삼각형 $\mathrm{ABQ}$에서 코사인법칙에 의하여
$\cos (\angle \mathrm{ABQ}) = \dfrac{\overline{\mathrm{AB}}^{2} + \overline{\mathrm{BQ}}^{2} -\,\overline{\mathrm{AQ}}^{2}}{2 \times \overline{\mathrm{AB}} \times \overline{\mathrm{BQ}}}$
삼각형 $\mathrm{ABC}$에서 코사인법칙에 의하여
$\overline{\mathrm{AC}}^{2} = \overline{\mathrm{AB}}^{2} + \overline{\mathrm{BC}}^{2} -\,2 \times \overline{\mathrm{AB}} \times \overline{\mathrm{BC}} \times \cos (\angle \mathrm{ABC})$
$= (2\sqrt{7})^{2} + 6^{2} -\,2 \times 2\sqrt{7} \times 6 \times \frac{\sqrt{7}}{4}$ $= 22$
이므로
$\overline{\mathrm{AC}} = \sqrt{22}$
이때 $\sin (\angle \mathrm{ABC}) = \sqrt{1 -\,\cos^{2} (\angle \mathrm{ABC})}$ $= \sqrt{1 -\,(\frac{\sqrt{7}}{4})^{2}} = \dfrac{3}{4}$이므로 삼각형 $\mathrm{ABC}$의 외접원의 반지름의 길이를 $R$이라 하면 삼각형 $\mathrm{ABC}$에서 사인법칙에 의하여
$\dfrac{\overline{\mathrm{AC}}}{\sin (\angle \mathrm{ABC})} = 2R$이므로
$R = \dfrac{\sqrt{22}}{2 \times \frac{3}{4}} = \dfrac{2\sqrt{22}}{3}$
따라서 삼각형 $\mathrm{ABC}$의 외접원의 넓이는
$\pi R^{2} = \pi \times (\frac{2\sqrt{22}}{3})^{2} = \dfrac{88}{9}\pi$
15. 상수 $k$와 $f^{\prime}(0) = 6$인 삼차함수 $f(x)$에 대하여 함수 $$g(x) = \begin{cases} \, f(x) + k & (|\,x\,| \gt 1) \\ \\ -f(x) & (|\,x\,| \le 1) \end{cases}$$ 이 다음 조건을 만족시킬 때, $k + f\bigg( \dfrac{1}{2}\bigg)$의 값은? [4점]
(가) 모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a+}\frac{g(x) - g(a)}{x - a}$의 값이 존재하고 그 값은 $0$ 이하이다.
(나) $x$에 대한 방정식 $g(x) = t$의 서로 다른 실근의 개수가 $2$가 되도록 하는 실수 $t$의 최댓값은 $13$이다.
① $\frac{15}{4}$
② $\frac{27}{4}$
③ $\frac{39}{4}$
④ $\frac{51}{4}$
⑤ $\frac{63}{4}$
①
삼차함수 $f(x)$를 $f(x) = ax^{3} + bx^{2} + cx + d$ ($a$, $b$, $c$, $d$는 상수)이라 하자.
$f'(x) = 3ax^{2} + 2bx + c$
$f'(0) = c$이므로 $c = 6$
$f'(x) = 3ax^{2} + 2bx + 6$ $\cdots\cdots$ ㉠
$x \ne -1$, $x \ne 1$인 모든 실수 $x$에 대하여 함수 $g(x)$는 미분가능하고
$x \lt -1$ 또는 $x \gt 1$에서 $g'(x) = f'(x)$,
$-1 \lt x \lt 1$에서 $g'(x) = -f'(x)$ $\cdots\cdots$ ㉡
이다.
조건 (가)에서 모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a+}\frac{g(x) -\,g(a)}{x -\,a}$의 값이 존재하므로
$a \ne -1$, $a \ne 1$에서
$\displaystyle \lim_{x \to a+}\frac{g(x) -\,g(a)}{x -\,a} = \lim_{x \to a}\frac{g(x) -\,g(a)}{x -\,a} = g'(a)$
모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a+}\frac{g(x) -\,g(a)}{x -\,a}$의 값이 $0$ 이하이므로
㉡에서 함수 $f(x)$는
$x \lt -1$ 또는 $x \gt 1$에서 $f'(x) \le 0$
$-1 \lt x \lt 1$에서 $f'(x) \ge 0$
을 만족시킨다.
함수 $f(x)$는 $x = -1$과 $x = 1$에서 모두 극값을 가지므로 $f'(-1) = f'(1) = 0$이어야 한다.
㉠에서 $f'(x) = 3ax^{2} + 2bx + 6 = 3a(x + 1)(x -\,1)$
$3ax^{2} + 2bx + 6 = 3ax^{2} -\,3a$
양변의 일차항 계수와 상수항을 비교하면
$2b = 0$에서 $b = 0$
$6 = -3a$에서 $a = -2$
$f(x) = -2x^{3} + 6x + d$
조건 (가)에서 $\displaystyle \lim_{x \to 1+}\frac{g(x) -\,g(1)}{x -\,1}$의 값이 존재하고
$x \to 1+$일 때 (분모)$\,\to 0$이므로 (분자)$\,\to 0$이다.
즉, $\displaystyle \lim_{x \to 1+}g(x) = g(1)$ $\cdots\cdots$ ㉢
$\displaystyle \lim_{x \to 1+}\{ f(x) + k\} = -f(1)$
$f(1) + k = -f(1)$이므로 $f(1) = -\frac{k}{2}$ $\cdots\cdots$ ㉣
한편 $\displaystyle \lim_{x \to 1-}g(x) = \lim_{x \to 1-} \{ -f(x) \} = -f(1) = g(1)$이고
㉢에서 함수 $g(x)$는 $x = 1$에서 연속이므로 함수 $y = g(x)$의 그래프는 다음과 같다.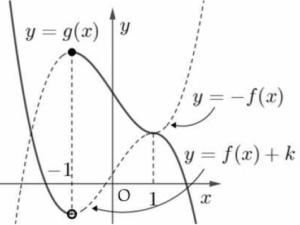 
조건 (나)에서 방정식 $g(x) = t$의 서로 다른 실근의 개수가 $2$가 되도록 하는 실수 $t$의 최댓값이 $13$이므로
$g(-1) = -f(-1) = 13$
$f(-1) = 2 -\,6 + d = -13$이므로 $d = -9$
$f(x) = -2x^{3} + 6x -\,9$
㉣에서 $f(1) = -2 + 6 -\,9 = -\frac{k}{2}$
$k = 10$
따라서 $k + f\bigg( \dfrac{1}{2}\bigg) = 10 + \bigg( -\dfrac{1}{4} + 3 -\,9\bigg) = \dfrac{15}{4}$
16. 방정식 $\log_{5}(x + 1) + \log_{5}(x -\,1) = \log_{25}9$를 만족시키는 실수 $x$의 값을 구하시오. [3점]
19. 상수 $a$에 대하여 함수 $f(x) = 3x^{3} -\,9x^{2} + a$의 극댓값이 $20$일 때, 함수 $f(x)$의 극솟값을 구하시오. [3점]
20. 실수 전체의 집합에서 정의된 함수 $f(x)$가 다음 조건을 만족시킨다.
$0 \le x \lt 4$일 때 $f(x) = -x^{2} + 4x$이고,
모든 실수 $x$에 대하여 $f(x + 4) = f(x)$이다.
방정식 $f(f(x)) = f(x)$의 $0$ 이상인 모든 실근을 작은 수부터 크기순으로 나열할 때, $n$번째 수를 $a_n$이라 하자. 다음은 $a_{20} + a_{21} + a_{22}$ 의 값을 구하는 과정이다.
방정식 $f(x) = x$의 모든 실근이 $0$, $3$이므로 방정식 $f(f(x)) = f(x)$의 실근을 구하는 것은 방정식 $f(x) \times (f(x) -\,3) = 0$의 실근을 구하는 것과 같다.
$0 \le x \lt 4$일 때, 방정식 $f(x) \times (f(x) -\,3) = 0$의 모든 실근은 $0$, $\fbox{$\textbf{ (가) }$}$, $3$이므로
$a_{1} = 0$, $a_{2} = \fbox{$\textbf{ (가) }$}\,$, $a_{3} = 3$
이다. 또한 모든 실수 $x$에 대하여 $f(x + 4) = f(x)$이므로
세 수열 $\{ a_{3n-2}\}$, $\{ a_{3n-1}\}$, $\{ a_{3n}\}$은
첫째항이 각각 $0$, $\fbox{$\textbf{ (가) }$}$, $3$이고
공차가 모두 $\fbox{$\textbf{ (나) }$}$인 등차수열이다.
따라서 $a_{20} + a_{21} + a_{22} = \fbox{$\textbf{ (다) }$}$이다.
위의 (가), (나), (다)에 알맞은 수를 각각 $p$, $q$, $r$이라 할 때, $p + q + r$의 값을 구하시오. [4점]
$85$
$0 \le x \le 4$일 때 $f(x) = -x^{2} + 4x$이고 모든 실수 $x$에 대하여 $f(x + 4) = f(x)$이므로 함수 $y = f(x)$의 그래프는 다음과 같다.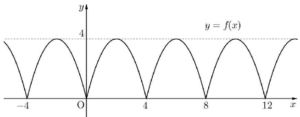 
방정식 $f(x) = x$에서 $-x^{2} + 4x = x$
$x(x -\,3) = 0$
$x = 0$ 또는 $x = 3$
방정식 $f(x) = x$의 모든 실근이 $0$, $3$이므로 방정식 $f(f(x)) = f(x)$의 실근을 구하는 것은 방정식 $f(x) \times (f(x) -\,3) = 0$의 실근을 구하는 것과 같다.
$0 \le x \le 4$일 때, $f(x) = 0$에서 $x = 0$
$f(x) = 3$에서 $-x^{2} + 4x = 3$
$(x -\,1)(x -\,3) = 0$
$x = 1$ 또는 $x = 3$
그러므로 $0 \le x \le 4$일 때, 방정식 $f(x) \times (f(x) -\,3) = 0$의 모든 실근은 $0$, $\fbox{ 1 }$, $3$이므로
$a_{1} = 0$, $a_{2} = \fbox{ 1 }$, $a_{3} = 3$이다.
또한 모든 실수 $x$에 대하여 $f(x + 4) = f(x)$이므로 세 수열 $\{ a_{3n-2}\}$, $\{ a_{3n-1}\}$, $\{ a_{3n}\}$은 첫째항이 각각 $0$, $\fbox{ 1 }$, $3$이고, 공차가 모두 $\fbox{ 4 }$인 등차수열이다.
따라서 $a_{20} = a_{3 \times 7-1} = 1 + 6 \times 4 = 25$
$a_{21} = a_{3 \times 7} = 3 + 6 \times 4 = 27$
$a_{22} = a_{3 \times 8-2} = 0 + 7 \times 4 = 28$
이므로
$a_{20} + a_{21} + a_{22} = 25 + 27 + 28 = \fbox{ 80 }$이다.
이때 $p = 1$, $q = 4$, $r = 80$이므로
$p + q + r = 85$
21. 함수 $f(x) = (x -\,1)(x -\,2)$와 최고차항의 계수가 $1$인 사차함수 $g(x)$가 다음 조건을 만족시킨다.
모든 실수 $x$에 대하여
$\displaystyle \lim_{x \to a}\frac{g(x) \times |\,f(x)\,|}{f(x)}$의 값과 $\displaystyle \lim_{x \to a}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$의 값이
모두 존재한다.
$g(-1)$의 값을 구하시오. [4점]
$42$
$f(x) = (x -\,1)(x -\,2)$
(ⅰ) $a \lt 1$ 또는 $a \gt 2$일 때,
$\displaystyle \lim_{x \to a}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to a}\frac{g(x) \times f(x)}{f(x)} = \lim_{x \to a}g(x) = g(a)$
(ⅱ) $1 \lt a \lt 2$일 때,
$\displaystyle \lim_{x \to a}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to a}\frac{g(x) \times (-f(x))}{f(x)} = -\lim_{x \to a}g(x) = -g(a)$
(ⅲ) $a = 1$일 때,
$\displaystyle \lim_{x \to 1-}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to 1-}\frac{g(x) \times f(x)}{f(x)} = \lim_{x \to 1-}g(x) = g(1)$
$\displaystyle \lim_{x \to 1+}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to 1+}\frac{g(x) \times (-f(x))}{f(x)} = -\lim_{x \to 1+}g(x) = -g(1)$
$a = 1$에서 $\displaystyle \lim_{x \to 1}\frac{g(x) \times |\,f(x)\,|}{f(x)}$의 극한값이 존재해야 하므로
$\displaystyle \lim_{x \to 1-}\frac{g(x) \times |\,f(x)\,|}{f(x)} = \lim_{x \to 1+}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
이어야 한다.
즉, $g(1) = -g(1)$이므로 $g(1) = 0$ $\cdots\cdots$ ㉠
(ⅳ) $a = 2$일 때,
$\displaystyle \lim_{x \to 2-}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to 2-}\frac{g(x) \times (-f(x))}{f(x)} = -\lim_{x \to 2-}g(x) = -g(2)$
$\displaystyle \lim_{x \to 2+}\frac{g(x) \times |\,f(x)\,|}{f(x)}$
$= \displaystyle \lim_{x \to 2+}\frac{g(x) \times f(x)}{f(x)} = \lim_{x \to 2+}g(x) = g(2)$
$a = 2$에서 $\displaystyle \lim_{x \to 2}\frac{g(x) \times |\,f(x)\,|}{f(x)}$의 극한값이 존재해야 하므로
$\displaystyle \lim_{x \to 2-}\frac{g(x) \times |\,f(x)\,|}{f(x)} = \lim_{x \to 2+}\frac{g(x) \times |\,f(x)\,|}{f(x)}$이어야 한다.
즉, $-g(2) = g(2)$이므로 $g(2) = 0$ $\cdots\cdots$ ㉡
(ⅰ) ~ (ⅳ)에서
모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a}\frac{g(x) \times |\,f(x)\,|}{f(x)}$의 극한값이 존재하려면
㉠, ㉡에서 $g(1) = g(2) = 0$이어야 한다.
이때, 함수 $g(x)$는 최고차항의 계수가 $1$인 사차함수이므로 $g(x) = f(x)h(x)$
(단, $h(x)$는 최고차항의 계수가 $1$인 이차함수)로 놓을 수 있다.
한편,
$\displaystyle \lim_{x \to a}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to a}\frac{|\,f(x)h(x) -\,f(x)\,|}{f(x)}h(x)$
$= \displaystyle \lim_{x \to a}\frac{|\,f(x)\,| \times |\,h(x) -\,1\,|}{f(x)h(x)}$
(ⅴ) $a \lt 1$ 또는 $a \gt 2$일 때,
$\displaystyle \lim_{x \to a}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to a}\frac{f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle \lim_{x \to a}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(a) = 0$이면 극한값이 존재하지 않으므로 $h(a) \ne 0$이고
$\displaystyle \lim_{x \to a}\frac{|\,h(x) -\,1\,|}{h(x)} = \frac{|\,h(a) -\,1\,|}{h(a)}$
(ⅵ) $1 \lt a \lt 2$일 때,
$\displaystyle \lim_{x \to a}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to a}\frac{-f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle -\lim_{x \to a}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(a) = 0$이면 극한값이 존재하지 않으므로 $h(a) \ne 0$이고
$\displaystyle -\lim_{x \to a}\frac{|\,h(x) -\,1\,|}{h(x)} = -\frac{|\,h(a) -\,1\,|}{h(a)}$
(ⅶ) $a = 1$일 때,
$\displaystyle \lim_{x \to 1-}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to 1-}\frac{f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle \lim_{x \to 1-}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(1) = 0$이면 극한값이 존재하지 않으므로 $h(1) \ne 0$이고
$\displaystyle \lim_{x \to 1-}\frac{|\,h(x) -\,1\,|}{h(x)} = \frac{|\,h(1) -\,1\,|}{h(1)}$,
$\displaystyle \lim_{x \to 1+}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to 1+}\frac{-f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle -\lim_{x \to 1+}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(1) = 0$이면 극한값이 존재하지 않으므로 $h(1) \ne 0$이고
$\displaystyle -\lim_{x \to 1+}\frac{|\,h(x) -\,1\,|}{h(x)} = -\frac{|\,h(1) -\,1\,|}{h(1)}$
$a = 1$에서 $\displaystyle \lim_{x \to 1}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$의 극한값이 존재해야 하므로
$\displaystyle \lim_{x \to 1-}\frac{|\,g(x) -\,f(x)\,|}{g(x)} = \lim_{x \to 1+}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$이어야 한다.
즉, $\frac{|\,h(1) -\,1\,|}{h(1)} = -\frac{|\,h(1) -\,1\,|}{h(1)}$이므로
$|\,h(1) -\,1\,| = -|\,h(1) -\,1\,|$
$h(1) = 1$ $\cdots\cdots$ ㉢
이다.
(ⅷ) $a = 2$일 때,
$\displaystyle \lim_{x \to 2-}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to 2-}\frac{-f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle -\lim_{x \to 2-}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(2) = 0$이면 극한값이 존재하지 않으므로 $h(2) \ne 0$이고
$\displaystyle -\lim_{x \to 2-}\frac{|\,h(x) -\,1\,|}{h(x)} = -\frac{|\,h(2) -\,1\,|}{h(2)}$,
$\displaystyle \lim_{x \to 2+}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$
$= \displaystyle \lim_{x \to 2+}\frac{f(x) \times |\,h(x) -\,1\,|}{f(x)h(x)}$
$= \displaystyle \lim_{x \to 2+}\frac{|\,h(x) -\,1\,|}{h(x)}$
이때, $h(2) = 0$이면 극한값이 존재하지 않으므로 $h(2) \ne 0$이고
$\displaystyle \lim_{x \to 2+}\frac{|\,h(x) -\,1\,|}{h(x)} = \frac{|\,h(2) -\,1\,|}{h(2)}$
$a = 2$에서 $\displaystyle \lim_{x \to 2}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$의 극한값이 존재해야 하므로
$\displaystyle \lim_{x \to 2-}\frac{|\,g(x) -\,f(x)\,|}{g(x)} = \lim_{x \to 2+}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$이어야 한다.
즉, $-\frac{|\,h(2) -\,1\,|}{h(2)} = \frac{|\,h(2) -\,1\,|}{h(2)}$이므로
$-|\,h(2) -\,1\,| = |\,h(2) -\,1\,|$
$h(2) = 1$ $\cdots\cdots$ ㉣
이다.
(ⅴ) ~ (ⅷ)에서
모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a}\frac{|\,g(x) -\,f(x)\,|}{g(x)}$의 극한값이 존재하려면 ㉢, ㉣에서
$h(1) = h(2) = 1$
이어야 한다.
이때, 함수 $h(x)$는 최고차항의 계수가 $1$인 이차함수이므로
$h(x) -\,1 = (x -\,1)(x -\,2)$ 즉, $h(x) = (x -\,1)(x -\,2) + 1$
따라서 $g(x) = f(x) \times (f(x) + 1)$이고,
$f(-1) = (-1 -\,1)(-1 -\,2) = 6$이므로
$g(-1) = 6 \times (6 + 1) = 42$
22. $k \gt 1$인 실수 $k$에 대하여 두 곡선 $$y = 2^{x} + \frac{k}{2}, \:\,y = k \times \bigg( \frac{1}{2}\bigg)^{x} + k - 2$$ 가 만나는 점을 $\mathrm{A}$라 하고, 점 $\mathrm{A}$를 지나고 기울기가 $-1$인 직선이 곡선 $y = 2^{x-2} -\,3$과 만나는 점을 $\mathrm{B}$라 하자. 삼각형 $\mathrm{AOB}$의 넓이가 $16$일 때, $k + \log_{2}k = \dfrac{q}{p}$이다. $p + q$의 값을 구하시오. (단, $\mathrm{O}$는 원점이고, $p$와 $q$는 서로소인 자연수이다.) [4점]
$35$
두 곡선 $y = 2^{x} + \frac{k}{2}$, $y = k \times ( \frac{1}{2})^{x} + k -\, 2$가 만나는 점 $\mathrm{A}$의 $x\,$좌표를 $a$라 하면
$2^{a} + \frac{k}{2} = k \times ( \frac{1}{2})^{a} + k -\,2$
$2^{a} = t$ ($t \gt 0$)라 하면
$t + \frac{k}{2} = \frac{k}{t} + k -\,2$
$2t^{2} + (4 -\,k)t -\,2k = 0$, $(t + 2)(2t -\,k) = 0$
$t \gt 0$이므로 $t = \frac{k}{2}$
즉, $2^{a} = \frac{k}{2}$이므로 $a = \log_{2}\frac{k}{2}$이고,
$2^{\log_{2}\frac{k}{2}} + \frac{k}{2} = \frac{k}{2} + \frac{k}{2} = k$이므로
점 $\mathrm{A}$의 좌표는 $\bigg(\log_{2}\dfrac{k}{2}, \,k \bigg)$이다.
이때, 실수 $k$에 대하여 $2^{\log_{2}\frac{k}{2}} = \frac{k}{2}$이므로 점 $\mathrm{A}$는 곡선 $2^{x} = \frac{y}{2}$, 즉 $y = 2^{x + 1}$ 위를 움직인다.
한편, 곡선 $y = 2^{x-2} -\,3$은 곡선 $y = 2^{x + 1}$을 $x\,$축의 방향으로 $3$ 만큼, $y\,$축의 방향으로 $-3$ 만큼 평행이동한 것이므로 점 $\mathrm{A}$를 지나고 기울기가 $-1$인 직선이 곡선 $y = 2^{x-2} -\,3$과 만나는 점 $\mathrm{B}$의 좌표는 $\bigg(\log_{2}\dfrac{k}{2} + 3, \,k -\,3 \bigg)$이고,
두 점 $\mathrm{A}$, $\mathrm{B}$사이의 거리는
$\sqrt{3^{2} + (-3)^{2}} = 3\sqrt{2}$
이다.
이때 원점 $\mathrm{O}$에서 직선 $\mathrm{AB}$까지의 거리를 $h$라 하면 삼각형 $\mathrm{OAB}$의 넓이가 $16$이므로
$\frac{1}{2} \times 3\sqrt{2} \times h = 16$에서 $h = \dfrac{16\sqrt{2}}{3}$이다.
한편, 직선 $\mathrm{AB}$의 방정식은
$y = -(x -\,\log_{2}\frac{k}{2}) + k$
즉, $x + y -\,k -\,\log_{2}\frac{k}{2} = 0$이고 원점과 직선 $\mathrm{AB}$ 사이의 거리가 $\frac{16\sqrt{2}}{3}$이므로
$\dfrac{|\,-k -\,\log_{2}\frac{k}{2}\,|}{\sqrt{2}} = \frac{16\sqrt{2}}{3}$
$|\,-k -\,\log_{2}\frac{k}{2}\,| = \frac{32}{3}$
$k + \log_{2}k -\,1 = \frac{32}{3}$
$k \gt 1$이므로 $k + \log_{2}k = \frac{35}{3}$
따라서 $p = 3$, $q = 35$이므로 $p + q = 35$
수학 영역(확률과 통계)
24. 두 사건 $A$와 $B$는 서로 배반사건이고 $$\mathrm{P}(A \cup B) = 1, \:\,\mathrm{P}(A^{c}) = 2\mathrm{P}(A)$$ 일 때, $\mathrm{P}(B)$의 값은? [3점]
① $\frac{1}{6}$
② $\frac{1}{3}$
③ $\frac{1}{2}$
④ $\frac{2}{3}$
⑤ $\frac{5}{6}$
④
두 사건 $A$와 $B$가 서로 배반사건이므로
$\mathrm{P}(A \cap B) = 0$
$\mathrm{P}(A \cup B) = \mathrm{P}(A) + \mathrm{P}(B) -\,\mathrm{P}(A \cap B)$
$ = \mathrm{P}(A) + \mathrm{P}(B) = 1$
$\mathrm{P}(A^{c}) = 2\mathrm{P}(A)$에서
$1 -\,\mathrm{P}(A) = 2\mathrm{P}(A)$
$\mathrm{P}(A) = \frac{1}{3}$
따라서 $\mathrm{P}(B) = 1 -\,\mathrm{P}(A)$ $= 1 -\,\frac{1}{3} = \dfrac{2}{3}$
25. 다항식 $(2x -\,1)^{5}(x + 1)$의 전개식에서 $x^{3}$의 계수는? [3점]
① $30$
② $35$
③ $40$
④ $45$
⑤ $50$
③
$(2x -\,1)^{5}(x + 1) = (2x -\,1)^{5} \times x + (2x -\,1)^{5}$이므로
다항식 $(2x -\,1)^{5}(x + 1)$의 전개식에서 $x^{3}$의 계수는 $(2x -\,1)^{5}$의 전개식에서 $x^{2}$의 계수와 $x^{3}$의 계수의 합과 같다.
$(2x -\,1)^{5}$의 전개식의 일반항은
${}_{5}\mathrm{C}_{r}(2x)^{5-r}(-1)^{r} = {}_{5}\mathrm{C}_{r}2^{5-r}(-1)^{r}x^{5-r}$ ($r = 0, 1, 2, \cdots, 5$)
$x^{2}$항은 $r = 3$일 때이고
$x^{3}$항은 $r = 2$일 때이므로
$x^{2}$의 계수와 $x^{3}$의 계수의 합은
${}_{5}\mathrm{C}_{3}2^{2}(-1)^{3} + {}_{5}\mathrm{C}_{2}2^{3}(-1)^{2}$
$= \frac{5 \times 4 \times 3}{3 \times 2 \times 1} \times (-4) + \frac{5 \times 4}{2 \times 1} \times 8$ $= 40$
26. 숫자 $1$, $2$, $3$, $4$, $5$, $6$, $7$이 하나씩 적혀 있는 $7$ 장의 카드가 있다. 이 $7$ 장의 카드를 모두 한 번씩 사용하여 일렬로 임의로 나열할 때, 양 끝에 놓인 카드에 적힌 두 수의 곱이 짝수가 되도록 카드가 놓일 확률은? [3점]
① $\frac{3}{7}$
② $\frac{1}{2}$
③ $\frac{4}{7}$
④ $\frac{9}{14}$
⑤ $\frac{5}{7}$
⑤
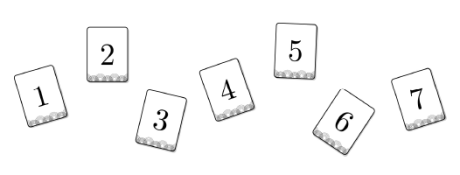
$7$ 장의 카드를 모두 한 번씩 사용하여 일렬로 임의로 나열할 때, 양 끝에 놓인 카드에 적힌 두 수의 곱이 짝수인 사건을 $A$라 하면 양 끝에 놓인 카드에 적힌 두 수의 곱이 홀수인 사건은 $A^{c}$이다.
양 끝에 놓인 카드에 적힌 두 수의 곱이 홀수가 되도록 $7$ 장의 카드를 모두 한 번씩 사용하여 일렬로 나열하는 경우의 수는 홀수 $1$, $3$, $5$, $7$이 적혀 있는 $4$ 장의 카드 중에서 서로 다른 $2$ 장의 카드를 택하여 양 끝에 나열한 후, 나머지 $5$ 장의 카드를 나열된 홀수가 적힌 $2$ 장의 카드 사이에 모두 한 번씩 사용하여 일렬로 나열하는 경우의 수와 같으므로
$\mathrm{P}(A^{c}) = \dfrac{{}_{4}\mathrm{P}_{2} \times 5!}{7!}$
$= \frac{(4 \times 3) \times 5!}{7!} = \frac{4 \times 3}{7 \times 6} = \frac{2}{7}$
따라서 $\mathrm{P}(A) = 1 -\,\mathrm{P}(A^{c})$ $= 1 – \frac{2}{7}$ $= \dfrac{5}{7}$
27. $5$ 명이 둘러앉을 수 있는 원 모양의 탁자와 남학생 $5$ 명, 여학생 $3$ 명이 있다. 이 $8$ 명의 학생 중에서 $4$ 명 이상의 남학생을 포함하여 $5$ 명의 학생을 선택하고 이 $5$ 명의 학생 모두를 일정한 간격으로 탁자에 둘러앉게 하는 경우의 수는? (단, 회전하여 일치하는 것은 같은 것으로 본다.) [3점]
① $384$
② $408$
③ $432$
④ $456$
⑤ $480$
①
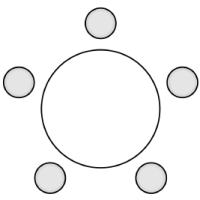
남학생 $4$명, 여학생 $1$명을 선택한 경우의 수는
${}_{5}\mathrm{C}_{4} \times {}_{3}\mathrm{C}_{1} = {}_{5}\mathrm{C}_{1} \times {}_{3}\mathrm{C}_{1}$ $= 5 \times 3 = 15$
남학생 $5$명을 선택한 경우의 수는
${}_{5}\mathrm{C}_{5} = 1$
선택한 $5$명의 학생을 원 모양의 탁자에 모두 둘러앉게 하는 경우의 수는
$(5 -\,1)! = 4! = 24$
따라서 구하는 경우의 수는 $(15 + 1) \times 24 = 384$
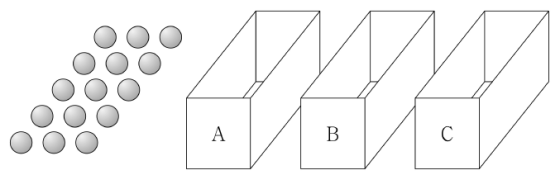
28. 공 $15$ 개와 비어 있는 세 상자 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$가 있다. 한 개의 주사위를 사용하여 다음 규칙에 따라 세 상자 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에 공을 넣는 시행을 한다.
주사위를 한 번 던져
나온 눈의 수가 $3$의 배수이면
세 상자 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에 넣는 공의 개수가 각각 $1$, $2$, $0$이고,
나온 눈의 수가 $3$ 의 배수가 아니면
세 상자 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에 넣는 공의 개수가 각각 $1$, $1$, $1$이다.
이 시행을 $5$ 번 반복한 후 상자 $\mathrm{B}$ 에 들어 있는 공의 개수가 홀수일 때, 상자 $\mathrm{A}$에 들어 있는 공의 개수와 상자 $\mathrm{C}$에 들어 있는 공의 개수의 합이 $8$ 이상일 확률은? [4점]
① $\frac{44}{61}$
② $\frac{47}{61}$
③ $\frac{50}{61}$
④ $\frac{53}{61}$
⑤ $\frac{56}{61}$
⑤
이 시행을 $5$번 반복한 후 상자 $\mathrm{B}$에 들어 있는 공의 개수가 홀수인 사건을 $X$, 상자 $\mathrm{A}$에 들어 있는 공의 개수와 상자 $\mathrm{C}$에 들어 있는 공의 개수의 합이 $8$ 이상인 사건을 $Y$라 하면 구하는 확률은 $\mathrm{P}(Y | X)$이다.
주사위를 한 번 던져 나온 눈의 수가 $3$의 배수일 확률은
$\frac{2}{6} = \frac{1}{3}$이고,
나온 눈의 수가 $3$의 배수가 아닐 확률은 $1 -\,\frac{1}{3} = \frac{2}{3}$이다.
이 시행을 $5$번 반복할 때, $3$의 배수의 눈이 나온 횟수를 $m$ ($m = 0, 1, 2, \cdots, 5$)
$3$의 배수가 아닌 눈이 나온 횟수를 $n$ ($n = 0, 1, 2, \cdots, 5$)라 하면
$m + n = 5$
이 시행을 $5$번 반복한 후 상자 $\mathrm{B}$에 들어 있는 공의 개수가 홀수이려면 $n$이 홀수이어야 한다. 즉,
$n = 1$ 또는 $n = 3$ 또는 $n = 5$
이다.
$n = 1$일 때, $m = 4$
$n = 3$일 때, $m = 2$
$n = 5$일 때, $m = 0$
이므로
$\mathrm{P}(X) = {}_{5}\mathrm{C}_{1}(\frac{2}{3})^{1}(\frac{1}{3})^{4} + {}_{5}\mathrm{C}_{3}(\frac{2}{3})^{3}(\frac{1}{3})^{2} + {}_{5}\mathrm{C}_{5}(\frac{2}{3})^{5}(\frac{1}{3})^{0}$
$= \frac{10}{3^{5}} + \frac{80}{3^{5}} + \frac{32}{3^{5}}$ $= \frac{122}{243}$
한편, $n = 1$, $m = 4$일 때,
상자 $\mathrm{A}$에 들어 있는 공의 개수와 상자 $\mathrm{C}$에 들어 있는 공의 개수의 합은 $5 + 1 = 6$
$n = 3$, $m = 2$일 때,
상자 $\mathrm{A}$에 들어 있는 공의 개수와 상자 $\mathrm{C}$에 들어 있는 공의 개수의 합은 $5 + 3 = 8$
$n = 5$, $m = 0$일 때,
상자 $\mathrm{A}$에 들어 있는 공의 개수와 상자 $\mathrm{C}$에 들어 있는 공의 개수의 합은 $5 + 5 = 10$
그러므로 사건 $X \cap Y$는
$n = 3$, $m = 2$ 또는 $n = 5$, $m = 0$
일 때이고,
$\mathrm{P}(X \cap Y) = {}_{5}\mathrm{C}_{3}(\frac{2}{3})^{3}(\frac{1}{3})^{2} + {}_{5}\mathrm{C}_{5}(\frac{2}{3})^{5}(\frac{1}{3})^{0}$
$= \frac{80}{3^{5}} + \frac{32}{3^{5}}$ $= \frac{112}{243}$
따라서 구하는 확률은
$\mathrm{P}(Y | X) = \dfrac{\mathrm{P}(X \cap Y)}{\mathrm{P}(X)}$
$= \dfrac{\frac{112}{243}}{\frac{122}{243}}$ $= \dfrac{56}{61}$
29. 한 개의 주사위를 세 번 던져서 나오는 눈의 수를 차례로 $a$, $b$, $c$라 할 때, $a + b = 8$ 또는 $b \ge c$일 확률은 $\dfrac{q}{p}$이다. $p + q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$44$
$a + b = 8$인 사건을 $X$, $b \ge c$인 사건을 $Y$라 하면
$a + b = 8$ 또는 $b \ge c$일 확률은 $\mathrm{P}(X \cap Y)$이고,
사건 $X \cap Y$는 $a + b = 8$이고 $b \ge c$인 사건이다.
(ⅰ) $a + b = 8$인 경우
$a + b = 8$을 만족시키는 두 수 $a$, $b$의 순서쌍 $(a, b)$는
$(2, 6)$, $(3, 5)$, $(4, 4)$, $(5, 3)$, $(6, 2)$
이다.
한편 $c$는 $1$부터 $6$까지 모든 수가 가능하므로
$\mathrm{P}(X) = \frac{5}{6^{2}} \times 1 = \frac{5}{36}$
(ⅱ) $b \ge c$인 경우
$b \ge c$를 만족시키는 두 수 $b$, $c$의 순서쌍 $(b, c)$의 개수는 $1$부터 $6$까지의 자연수 중에서 중복을 허락하여 2개를 선택하는 중복조합의 수와 같으므로
${}_{6}\mathrm{H}_{2} = {}_{6+2-1}\mathrm{C}_{2}$
$= {}_{7}\mathrm{C}_{2} = \frac{7 \times 6}{2 \times 1} = 21$
한편, $a$는 $1$부터 $6$까지 모든 수가 가능하므로
$\mathrm{P}(Y) = 1 \times \frac{21}{6^{2}} = \frac{7}{12}$
(ⅲ) $a + b = 8$이고 $b \ge c$인 경우
$a + b = 8$이고 $b \ge c$인 경우는 다음과 같다.
$a = 2$, $b = 6$일 때, $c$의 값은 $1$, $2$, $3$, $4$, $5$, $6$
$a = 3$, $b = 5$일 때, $c$의 값은 $1$, $2$, $3$, $4$, $5$
$a = 4$, $b = 4$일 때, $c$의 값은 $1$, $2$, $3$, $4$
$a = 5$, $b = 3$일 때, $c$의 값은 $1$, $2$, $3$
$a = 6$, $b = 2$일 때, $c$의 값은 $1$, $2$
그러므로
$\mathrm{P}(X \cap Y) = \frac{6 + 5 + 4 + 3 + 2}{6^{3}} = \frac{5}{54}$
(ⅰ), (ⅱ), (ⅲ)에서
$\mathrm{P}(X \cup Y) = \mathrm{P}(X) + \mathrm{P}(Y) -\,\mathrm{P}(X \cap Y)$
$= \frac{5}{36} + \frac{7}{12} -\,\frac{5}{54} = \frac{15 + 63 -\,10}{108}$ $= \dfrac{17}{27}$
따라서 $p = 27$, $q = 17$이므로 $p + q = 44$
30. 집합 $X = \{1, 2, 3, 4, 5 \}$에 대하여 다음 조건을 만족시키는 함수 $f : X \longrightarrow X$ 의 개수를 구하시오. [4점]
(가) $x = 1, 2, 3, 4$일 때 $f(x+1) + 3 \ge f(x) + x$이다.
(나) $f(2)$의 값은 홀수이다.
$115$
조건 (가)의 $x$에 $1$, $2$, $3$, $4$를 각각 대입하면
$f(2) + 3 \ge f(1) + 1$
$f(3) + 3 \ge f(2) + 2$
$f(4) + 3 \ge f(3) + 3$
$f(5) + 3 \ge f(4) + 4$
이므로
$1 \le f(1) \le f(2) + 2$, $f(2) -\,1 \le f(3) \le f(4)\le f(5) -\,1 \le 4$
조건 (나)에서 $f(2)$의 값은 홀수이므로 $f(2)$의 값은 $1$ 또는 $3$ 또는 $5$
(ⅰ) $f(2) = 1$인 경우
$1 \le f(1) \le 3$, $1 \le f(3) \le f(4)\le f(5) -\,1 \le 4$
이므로 $f(1)$의 값을 정하는 경우의 수는 $3$
$f(3)$, $f(4)$, $f(5) -\,1$의 값을 정하는 경우의 수는 $1$, $2$, $3$, $4$ 중에서 중복을 허락하여 $3$개를 선택하는 중복조합의 수와 같으므로
${}_{4}\mathrm{H}_{3} = {}_{4+3-1}\mathrm{C}_{3}$
$= {}_{6}\mathrm{C}_{3} = \frac{6 \times 5 \times 4}{3 \times 2 \times 1} = 20$
따라서 이 경우의 함수 $f$의 개수는 $3 \times 20 = 60$
(ⅱ) $f(2) = 3$인 경우
$1 \le f(1) \le 5$, $2 \le f(3) \le f(4)\le f(5) -\,1 \le 4$
이므로 $f(1)$의 값을 정하는 경우의 수는 $5$
$f(3)$, $f(4)$, $f(5) -\,1$의 값을 정하는 경우의 수는 $2$, $3$, $4$ 중에서 중복을 허락하여 $3$개를 선택하는 중복조합의 수와 같으므로
${}_{3}\mathrm{H}_{3} = {}_{3+3-1}\mathrm{C}_{3}$
$= {}_{5}\mathrm{C}_{3} = {}_{5}\mathrm{C}_{2} = \frac{5 \times 4}{2 \times 1} = 10$
따라서 이 경우의 함수 $f$의 개수는 $5 \times 10 = 50$
(ⅲ) $f(2) = 5$인 경우
$1 \le f(1) \le 5$, $4 \le f(3) \le f(4)\le f(5) -\,1 \le 4$
이므로 $f(1)$의 값을 정하는 경우의 수는 $5$
$f(3)$, $f(4)$, $f(5) -\,1$의 값은 모두 $4$이므로 경우의 수는 $1$
따라서 이 경우의 함수 $f$의 개수는 $5 \times 1 = 5$
(ⅰ), (ⅱ), (ⅲ)에서 구하는 함수 의 개수는
$60 + 50 + 5 = 115$
수학 영역(미적분)
23. $\displaystyle \lim_{n \to \infty}\frac{4 \times 3^{n+1}}{2^{n} + 3^{n}}$의 값은? [2점]
① $12$
② $13$
③ $14$
④ $15$
⑤ $16$
24. 곡선 $3x + y + \cos(xy) = 2$ 위의 점 $(0, 1)$에서의 접선의 $x\,$절편은? [3점]
① $\frac{1}{6}$
② $\frac{1}{3}$
③ $\frac{1}{2}$
④ $\frac{2}{3}$
⑤ $\frac{5}{6}$
②
$3x + y + \cos(xy) = 2$의 양변을 $x$에 대하여 미분하면
$3 + \frac{dy}{dx} -\,\sin(xy) \times (y + x\frac{dy}{dx}) = 0$
$\{ 1 -\,x \sin(xy)\}\frac{dy}{dx} = y \sin (xy -\,3)$
$\dfrac{dy}{dx} = \dfrac{y \sin (xy) -\,3}{1 -\,x \sin(xy)}$ (단, $1 -\,x \sin(xy) \ne 0$)
이때 $x = 0$, $y = 1$에서의 $\frac{dy}{dx}$의 값은 $\frac{0 -\,3}{1 -\,0} = -3$
이므로 구하는 접선의 방정식은 $y = -3x + 1$
따라서 이 접선의 $x$절편은 $-3x + 1 = 0$에서 $x = \dfrac{1}{3}$
25. 양수 $a$에 대하여 급수 $\displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{a -\,3n}{n} + \dfrac{an + 6}{n + a} \bigg)$이 실수 $S$에 수렴할 때, $a + S$의 값은? [3점]
① $7$
② $\frac{15}{2}$
③ $8$
④ $\frac{17}{2}$
⑤ $9$
④
급수 $\displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{a -\,3n}{n} + \dfrac{an + 6}{n + a} \bigg)$이 수렴하므로
$\displaystyle \lim_{n \to \infty}\bigg( \dfrac{a -\,3n}{n} + \dfrac{an + 6}{n + a} \bigg) = 0$
따라서
$\displaystyle \lim_{n \to \infty}\bigg( \dfrac{a -\,3n}{n} + \dfrac{an + 6}{n + a} \bigg)$
$= \lim_{n \to \infty}\bigg( \dfrac{a}{n} -\,3 + \dfrac{a + \frac{6}{n}}{1 + \frac{a}{n}} \bigg)$ $= 0 -\,3 + a = 0$
즉 $a = 3$
이때
$\displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{a -\,3n}{n} + \dfrac{an + 6}{n + a} \bigg)$
$= \displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{3 -\,3n}{n} + \dfrac{3n + 6}{n + 3} \bigg)$
$= \displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{3}{n} -\,3 + \dfrac{3(n + 3) -\,3}{n + 3} \bigg)$
$= \displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{3}{n} -\,3 + 3 -\, \dfrac{3}{n + 3} \bigg)$
$= \displaystyle 3\sum_{n = 1}^{\infty}\bigg( \dfrac{1}{n} -\, \dfrac{1}{n + 3} \bigg)$
이고
$\displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{1}{n} -\, \dfrac{1}{n + 3} \bigg)$
$= \displaystyle \lim_{n \to \infty} \sum_{k = 1}^{n}\bigg( \dfrac{1}{k} -\, \dfrac{1}{n + k} \bigg)$
$= \displaystyle \lim_{n \to \infty} \left\{\bigg(1 -\,\frac{1}{4} \bigg) + \bigg(\frac{1}{2} -\,\frac{1}{4} \bigg) + \bigg(\frac{1}{3} -\,\frac{1}{6} \bigg) \right\} +$
$\displaystyle \cdots + \bigg(\frac{1}{n -\,1} -\,\frac{1}{n + 2} \bigg) + \bigg(\frac{1}{n} -\,\frac{1}{n + 3} \bigg)$
$= \displaystyle \lim_{n \to \infty}\bigg(1 + \frac{1}{2} + \frac{1}{3} -\,\frac{1}{n + 1} -\,\frac{1}{n + 2} -\,\frac{1}{n + 3} \bigg)$
$= \displaystyle 1 + \frac{1}{2} + \frac{1}{3} = \frac{11}{6}$
따라서
$S = 3\displaystyle \sum_{n = 1}^{\infty}\bigg( \dfrac{1}{n} -\, \dfrac{1}{n + 3} \bigg)$ $= 3 \times \dfrac{11}{6} = \dfrac{11}{2}$
이므로
$a + S = 3 + \frac{11}{2} = \dfrac{17}{2}$
26. 함수 $f(x) = e^{3x} -\,3e^{2x} + 4e^{x}$의 역함수를 $g(x)$라 하자. $g^{\prime}(a) = \dfrac{1}{8}$이 되도록 하는 실수 $a$에 대하여 $a + f^{\prime}(g(a))$ 의 값은? [3점]
① $11$
② $12$
③ $13$
④ $14$
⑤ $15$
②
$g'(a) = \dfrac{1}{f'(g(a))} = \dfrac{1}{8}$
에서
$f'(g(a)) = 8$
이때 $f(x) = e^{3x} -\,3e^{2x} + 4e^{x}$에서
$f'(x) = 3e^{3x} -\,6e^{2x} + 4e^{x}$
이고
$g(a) = b$라 하면 $f'(g(a)) = f'(b) = 3e^{3b} -\,6e^{2b} + 4e^{b}$이고
$f'(g(a)) = 8$이므로
$3e^{3b} -\,6e^{2b} + 4e^{b} = 8$
$3e^{3b} -\,6e^{2b} + 4e^{b} -\,8 = 0$
$(e^{b} -\,2)(3e^{2b} + 4) = 0$
$e^{b} \gt 0$이므로 $e^{b} = 2$ 즉, $b = \ln 2$
$g(a) = b$에서 $a = f(b)$이므로
$a = f(\ln 2) = e^{3\ln 2} -\,3e^{2\ln 2} + 4e^{\ln 2}$
$= e^{\ln 8} -\,3e^{\ln 4} + 4e^{\ln 2}$
$= 8 -\,3 \times 4 + 4 \times 2$
$= 4$
따라서 $a + f'(g(a)) = 4 + 8 = 12$
27. 그림과 같이 길이가 $2$인 선분 $\mathrm{AB}$를 지름으로 하는 반원의 호 $\mathrm{AB}$ 위의 점 $\mathrm{P}$에 대하여 $\angle \mathrm{BAP} = \theta$ $\bigg(\dfrac{\pi}{4} \lt \theta \lt \dfrac{\pi}{2}\bigg)$라 하고, 점 $\mathrm{P}$를 지나고 선분 $\mathrm{AB}$에 평행한 직선이 호 $\mathrm{AB}$와 만나는 점 중 $\mathrm{P}$가 아닌 점을 $\mathrm{Q}$라 하자. 사각형 $\mathrm{ABQP}$의 넓이를 $f(\theta)$라 하고, $\overline{\mathrm{AP}} : \overline{\mathrm{BP}} = 1 : 3$이 되도록 하는 $\theta$의 값을 $a$라 할 때, $f^{\prime}(a)$의 값은? [3점]
① $-\frac{64}{25}$
② $-\frac{59}{25}$
③ $-\frac{54}{25}$
④ $-\frac{49}{25}$
⑤ $-\frac{44}{25}$
③
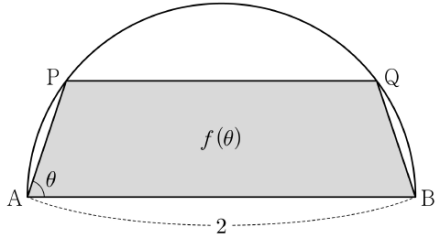
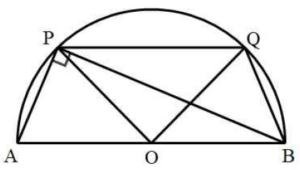선분 $\mathrm{AB}$의 중점을 $\mathrm{O}$라 하면 삼각형 $\mathrm{OPA}$는
$\overline{\mathrm{OP}} = \overline{\mathrm{OA}} = 1$, $\angle \mathrm{AOP} = \pi -\,2\theta$
인 이등변삼각형이다.
사각형 $\mathrm{ABQP}$는 원에 내접하는 사각형이므로 $\angle \mathrm{BQP} = \pi -\,\theta$이고,
선분 $\mathrm{AB}$와 선분 $\mathrm{PQ}$가 평행하므로 $\angle \mathrm{OBQ} = \theta$이다.
따라서 삼각형 $\mathrm{OBQ}$는
$\overline{\mathrm{OQ}} = \overline{\mathrm{OB}} = 1$, $\angle \mathrm{BOQ} = \pi -\,2\theta$인 이등변삼각형이다.
또, 삼각형 $\mathrm{OPQ}$는
$\overline{\mathrm{OP}} = \overline{\mathrm{OQ}} = 1$, $\angle \mathrm{POQ} = \pi -\,2(\pi -\,2\theta) = 4 \theta -\,\pi$인 이등변삼각형이다.
이때, 사각형 $\mathrm{ABQP}$의 넓이는
$f(\theta) = 2 \times \frac{1}{2} \times 1 \times 1 \times \sin(\pi -\,2\theta) + \frac{1}{2} \times 1 \times 1 \times \sin(4\theta -\,\pi)$
$= \sin(\pi -\,2\theta) + \frac{1}{2} \sin(4\theta -\,\pi)$
$= \sin2\theta + \frac{1}{2} \sin 4\theta$
이므로
$f'(\theta) = 2 \cos 2\theta -\,2 \cos 4\theta$
이다.
한편, $\overline{\mathrm{AP}} : \overline{\mathrm{BP}} = 1 : 3$일 때 삼각형 $\mathrm{ABP}$는 $\angle \mathrm{BAP} = a$, $\angle \mathrm{APB} = \frac{\pi}{2}$인 직각삼각형이므로
$\cos a = \frac{1}{\sqrt{10}}$
이다. 이때,
$\cos 2a = \cos (a + a) = \cos a \cos a -\,\sin a \sin a$
$= \cos^{2}a -\,\sin^{2}a = \cos^{2}a -\,( 1 -\,\cos^{2}a) = 2\cos^{2}a -\, 1$ $= 2 \times \frac{1}{10} -\,1 = -\frac{4}{5}$이고,
마찬가지 방법으로
$\cos 4a = \cos (2a + 2a) = 2 \cos^{2}2a -\,1 = 2 \times \frac{16}{25} -\,1 = \frac{7}{25}$
이므로
$f'(a) = 2 \cos 2a -\,2 \cos 4a$ $= 2 \times (-\frac{4}{5}) -\,2 \times \frac{7}{25} = -\dfrac{54}{25}$
28. 실수 전체의 집합에서 이계도함수를 갖는 함수 $f(x)$와 두 상수 $a$, $b$가 다음 조건을 만족시킬 때, $a \times e^{b}$의 값은? [4점]
(가) 모든 실수 $x$에 대하여
$$(f(x))^{5} + (f(x))^{3} + ax + b = \ln\bigg(x^{2} + x + \frac{5}{2} \bigg)$$
이다.
(나) $f(-3)f(3) \lt 0$, $f^{\prime}(2) \gt 0$
① $-3e^{-\frac{4}{3}}$
② $-\frac{5}{3}e^{-\frac{4}{3}}$
③ $-\frac{1}{3}e^{-\frac{4}{3}}$
④ $e^{-\frac{4}{3}}$
⑤ $\frac{7}{3}e^{-\frac{4}{3}}$
①
조건 (나)에서 $f(-3)f(3) \lt 0$이므로 사잇값의 정리에 의하여
$f(\alpha) = 0$ ($-3 \lt \alpha \lt 3$)
을 만족시키는 $\alpha$가 존재한다.
또한, 조건 (가)의 양변을 $x$에 대하여 미분하면
$5(f(x))^{4} \times f'(x) + 3(f(x))^{2} \times f'(x) + a = \dfrac{2x + 1}{x^{2} + x + \frac{5}{2}}$ $\cdots\cdots$ ㉠
다시 ㉠의 양변을 $x$에 대하여 미분하면
$20(f(x))^{3} \times (f'(x))^{2} + 5(f(x))^{4} \times f”(x) + 6f(x) \times (f'(x))^{3} + 3(f(x))^{2} \times f”(x)$
$= \dfrac{2(x^{2} + x + \frac{5}{2}) -\,(2x + 1)(2x + 1)}{(x^{2} + x + \frac{5}{2})^{2}}$
$20(f(x))^{3} \times (f'(x))^{2} + 5(f(x))^{4} \times f”(x) + 6f(x) \times (f'(x))^{3} + 3(f(x))^{2} \times f”(x)$
$= \dfrac{-2(x + 2)(x -\,1)}{(x^{2} + x + \frac{5}{2})^{2}}$ $\cdots\cdots$ ㉡
㉡은 $x$에 대한 항등식이므로 $x = \alpha$를 대입하면
$0 = \dfrac{-2(\alpha + 2)(\alpha -\,1)}{(\alpha^{2} + \alpha + \frac{5}{2})^{2}}$
따라서 $\alpha = -2$ 또는 $\alpha = 1$
(ⅰ) $\alpha = -2$일 때
㉠에 $x = \alpha = -2$를 대입하면
$ a = \frac{2(-2) + 1}{(-2)^{2} + (-2) + \frac{5}{2}} = \frac{-3}{\frac{9}{2}} = -\frac{2}{3}$
이때 ㉠에서
$5(f(x))^{4} \times f'(x) + 3(f(x))^{2} \times f'(x) = \frac{2x + 1}{x^{2} + x + \frac{5}{2}} + \frac{2}{3}$
이므로 $x = 2$를 대입하면
$5(f(2))^{4} \times f'(2) + 3(f(2))^{2} \times f'(2) = \frac{2 \times 2 + 1}{2^{2} + 2 + \frac{5}{2}} + \frac{2}{3}$ $= \frac{64}{51}$
즉
$5(f(2))^{4} \times f'(2) + 3(f(2))^{2} \times f'(2) = \dfrac{64}{51}$이고,
이것은 조건 (나)의 $f'(2) \gt 0$을 만족시킨다.
또, 조건 (가)에 $x = \alpha = -2$를 대입하면
$-\frac{2}{3} \times (-2) + b = \ln \{ (-2)^{2} + (-2) + \frac{5}{2} \}$
$\frac{4}{3} + b = \ln \frac{9}{2}$
$b = -\frac{4}{3} + \ln \frac{9}{2}$
(ⅱ) $\alpha = 1$일 때
㉠에 $x = \alpha = 1$을 대입하면
$ a = \frac{2 \times 1 + 1}{1 + 1 + \frac{5}{2}} = \frac{3}{\frac{9}{2}} = \frac{2}{3}$
이때 ㉠에서
$5(f(x))^{4} \times f'(x) + 3(f(x))^{2} \times f'(x) = \frac{2x + 1}{x^{2} + x + \frac{5}{2}} -\,\frac{2}{3}$
이므로 $x = 2$를 대입하면
$5(f(2))^{4} \times f'(2) + 3(f(2))^{2} \times f'(2) = \frac{2 \times 2 + 1}{2^{2} + 2 + \frac{5}{2}} -\,\frac{2}{3}$ $= -\frac{4}{51}$
즉
$5(f(2))^{4} \times f'(2) + 3(f(2))^{2} \times f'(2) = -\dfrac{4}{51}$
그런데 조건 (나)에서 $f'(2) \gt 0$이므로 (좌변)$\ge 0$, (우변)$\lt 0$
따라서 모순이다.
(ⅰ), (ⅱ)에 의하여
$a = -\frac{2}{3}$, $b = -\frac{4}{3} + \ln \frac{9}{2}$
이므로
$a \times e^{b} = -\frac{2}{3} \times e^{-\frac{4}{3} + \ln \frac{9}{2}}$
$= -\frac{2}{3} \times e^{-\frac{4}{3}} \times e^{\ln \frac{9}{2}}$
$= -\frac{2}{3} \times \frac{9}{2} \times e^{-\frac{4}{3}}$
$= -3e^{-\frac{4}{3}}$
29. 두 정수 $\alpha$, $\beta$ ($\alpha \gt \beta$)에 대하여 다음 조건을 만족시키는 수열 $\{ a_{n \}}$이 있다.
모든 자연수 $n$에 대하여 $$a_{n} = \alpha \times \sin \frac{n}{2}\pi + \beta \times \cos \frac{n}{2}\pi$$ 이고, $a_{1} \times a_{2} \times a_{3} \times a_{4} = 4 $이다.
수열 $\{ a_{n} \}$과 $b_{1} \gt 0$인 등비수열 $\{ b_{n} \}$에 대하여 $$\sum_{n = 1}^{\infty}(a_{4n-2}b_{n}) = \sum_{n = 1}^{\infty}(a_{4n-3}b_{2n}) = 6$$ 일 때, $b_{1} \times b_{3} = \dfrac{q}{p}$이다. $p + q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$109$
주어진 조건에 의하여
$a_{1} = \alpha \times \sin \frac{\pi}{2} + \beta \times \cos \frac{\pi}{2} = \alpha$
$a_{2} = \alpha \times \sin \pi + \beta \times \cos \pi = -\beta$
$a_{3} = \alpha \times \sin \frac{3}{2}\pi + \beta \times \cos \frac{3}{2}\pi = -\alpha$
$a_{4} = \alpha \times \sin 2\pi + \beta \times \cos 2\pi = \beta$
$a_{5} = \alpha$
$\:\:\vdots$
이므로
수열 $\{ a_{n} \}$은
$\alpha$, $-\beta$, $-\alpha$, $\beta$, $\alpha$, $-\beta$, $\cdots$
이다.
따라서 $a_{4n-2} = -\beta$, $a_{4n-3} = \alpha$이고
$a_{1} \times a_{2} \times a_{3} \times a_{4} = \alpha^{2}\beta^{2}= 4 $
에서
$\alpha\beta = -2$ 또는 $\alpha\beta = 2$
그런데 $\alpha$, $\beta$ ($\alpha \gt \beta$)는 정수이므로
$\alpha = 2, \:\beta = 1$ 또는 $\alpha = -1, \:\beta = -2$ 또는 $\alpha = 2, \:\beta = -1$ 또는 $\alpha = 1, \:\beta = -2$
이다.
이때, 등비수열 $\{ b_{n} \}$의 공비를 $r$이라 하면
$\displaystyle \sum_{n = 1}^{\infty}(a_{4n-2}b_{n}) = \sum_{n = 1}^{\infty}(a_{4n-3}b_{2n}) = 6$
$\displaystyle -\beta\sum_{n = 1}^{\infty}b_{n} = \alpha\sum_{n = 1}^{\infty}b_{2n} = 6$ $\cdots\cdots$ ㉠
이고 ㉠을 만족시키기 위해서는 $-1 \lt r \lt 1$이어야 한다.
따라서
$\displaystyle -\beta \times \frac{b_{1}}{1 -\,r} = \alpha \times \frac{b_{1}r}{1 -\,r^{2}} = 6$
(ⅰ) $\alpha = 2, \:\beta = 1$일 때
$-\frac{b_{1}}{1 -\,r} = 6$에서 $1 -\,r \gt 0$이므로 $b_{1} \lt 0$
이것은 $b_{1} \gt 0$을 만족시키지 않는다.
(ⅱ) $\alpha = -1, \:\beta = -2$일 때
$\displaystyle 2 \times \frac{b_{1}}{1 -\,r} = -\frac{b_{1}r}{1 -\,r^{2}} = 6$
이므로
$2 = \frac{-r}{1 + r}$, $2 + 2r = -r$, $r = -\frac{2}{3}$
따라서
$\dfrac{2b_{1}}{1 -\,(-\frac{2}{3})} = \dfrac{2b_{1}}{\frac{5}{3}} = \dfrac{6b_{1}}{5} = 6$
에서
$b_{1} = 5$
이므로
$b_{3} = b_{1}r^{2} = 5 \times (-\frac{2}{3})^{2} = \frac{20}{9}$
(ⅲ) $\alpha = 2, \:\beta = -1$일 때
$\displaystyle \frac{b_{1}}{1 -\,r} = 2 \times \frac{b_{1}r}{1 -\,r^{2}} = 6$
이므로
$1 = \frac{2r}{1 + r}$, $1 + r = 2r$, $r = 1$
이것은 $-1 \lt r \lt 1$을 만족시키지 않는다.
(ⅳ) $\alpha = 1, \:\beta = -2$일 때
$\displaystyle 2 \times \frac{b_{1}}{1 -\,r} = \frac{b_{1}r}{1 -\,r^{2}} = 6$
이므로
$2 = \frac{r}{1 + r}$, $2 + 2r = r$, $r = -2$
이것은 $-1 \lt r \lt 1$을 만족시키지 않는다.
(ⅰ) ~ (ⅳ)에서 $b_{1} = 5$, $b_{3} = \frac{20}{9}$이므로
$b_{1} \times b_{3} = 5 \times \frac{20}{9} = \frac{100}{9}$
따라서 $p = 9$, $q = 100$이므로
$p + q = 109$
30. 최고차항의 계수가 $1$인 삼차함수 $f(x)$에 대하여 함수 $$g(x) = \left|\, f\bigg( \frac{2}{1 + e^{-x}} \bigg)\, \right|$$ 가 실수 전체의 집합에서 미분가능하고 다음 조건을 만족시킨다.
(가) 함수 $g(x)$는 $x = 0$에서 극소이고, $g(0) \gt 0$이다.
(나) $g^{\prime}(\ln 3) \lt 0, \:\,|\,g^{\prime}(-\ln 3)\,| = \dfrac{3}{8}g(-\ln 3)$
$g(0)$의 최솟값을 $\dfrac{q}{p}$라 할 때, $p + q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$25$
$h(x) = \dfrac{2}{1 + e^{-x}}$라 하면
$\displaystyle \lim_{x \to \infty}h(x) = \lim_{x \to \infty}\frac{2}{1 + e^{-x}} = 2$
$\displaystyle \lim_{x \to -\infty}h(x) = \lim_{x \to -\infty}\frac{2}{1 + e^{-x}} = 0$
이고,
$h'(x) = \dfrac{2e^{-x}}{(1 + e^{-x})^{2}} \gt 0$
이므로
$0 \lt h(x) \lt 2$
이다.
$f(h(x)) \gt 0$일 때, $g(x) = f(h(x))$이므로
$g'(x) = f'(h(x))h'(x)$이고,
$f(h(x)) \lt 0$일 때, $g(x) = -f(h(x))$이므로
$g'(x) = -f'(h(x))h'(x)$
함수 $g(x)$가 실수 전체의 집합에서 미분가능하고 조건 (가)에 의하여 에서
극소이므로
$g'(0) = 0$
이때, $g(0) \gt 0$이므로
$f(h(0)) \gt 0$ 또는 $f(h(0)) \lt 0$ $\cdots\cdots$ ㉠
그러므로
$g'(0) = f'(h(0))h'(0) = \frac{1}{2}f'(1)$
또는
$g'(0) = -f'(h(0))h'(0) = -\frac{1}{2}f'(1)$
이므로 $g'(0) = 0$이려면 $f'(1) = 0$이어야 한다.
또, $g'(x) = f'(h(x))h'(x)$ 또는 $g'(x) = -f'(h(x))h'(x)$에서 모든 실수 $x$에 대하여 $h'(x) \gt 0$이고, 함수 $g'(x)$의 부호가 $x = 0$의 좌우에서 바뀌므로 $f'(x)$의 부호가 $x = h(0) = 1$의 좌우에서 바뀐다.
즉, 삼차함수 $f(x)$가 $x = 1$에서 극값을 가져야 하고 ㉠에서 $f(1) \gt 0$ 또는 $f(1) \lt 0$이다.
만일 함수 $f(x)$가 $x = 1$에서 극소이면 함수 $g(x)$가 $x = 0$에서 극소이고, 함수 $|\,f(h(x))\,|$가 실수 전체의 집합에서 미분가능하므로 그림과 같이 $f(1) \gt 0$이어야 한다.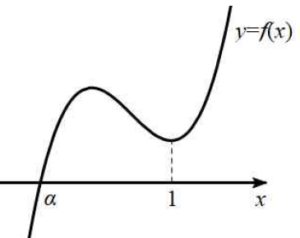
또, $f(\alpha) = 0$이고 $h(x) = \alpha$인 $x$가 존재하면 함수 $g(x)$가 $h(x) = \alpha$인 $x$에서 미분가능하지 않으므로 $\alpha \le 0$이어야 한다.
이때 $0 \lt h(x) \lt 2$에서 $f(h(x)) \lt 0$이므로 $g(x) = f(h(x))$이고,
$g'(x) = f'(h(x))h'(x) = f'(\frac{2}{1 + e^{-x}}) \times \frac{2e^{-x}}{(1 + e^{-x})^{2}}$
이 경우
$g'(\ln 3) = f'(\frac{2}{1 + \frac{1}{3}}) \times \frac{\frac{2}{3}}{(1 + \frac{1}{3})^{2}} = f'(\frac{3}{2}) \times \frac{3}{8}$
에서 $f'(\frac{3}{2}) \gt 0$이므로 $g'(\ln 3) \gt 0$이다.
이것은 조건 (나)를 만족시키지 않는다.
그러므로 함수 $f(x)$는 $x = 1$에서 극대이고, 이 경우 함수 $g(x)$가 $x = 0$에서 극소이고 함수 $|\,f(h(x))\,|$가 실수 전체의 집합에서 미분가능하므로 그림과 같이 $f(1) \lt 0$이어야 한다.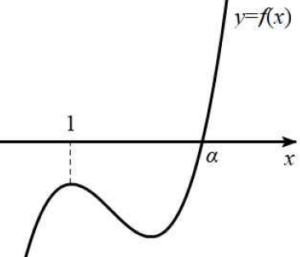
마찬가지로 $f(\alpha) = 0$이고 $h(x) = \alpha$인 $x$가 존재하면 함수 $g(x)$가 $h(x) = \alpha$인 $x$에서 미분가능하지 않으므로 $\alpha \le 2$이어야 한다.
이때 $0 \lt h(x) \lt 2$에서 $f(h(x)) \lt 0$이므로 $g(x) = -f(h(x))$이고,
$g'(x) = -f'(h(x))h'(x) = -f'(\frac{2}{1 + e^{-x}}) \times \frac{2e^{-x}}{(1 + e^{-x})^{2}}$
이 경우
$g'(\ln 3) = -f'(\frac{2}{1 + \frac{1}{3}}) \times \frac{\frac{2}{3}}{(1 + \frac{1}{3})^{2}} = -f'(\frac{3}{2}) \times \frac{3}{8}$
이므로 $f'(\frac{3}{2}) \gt 0$이면 조건 (나)의 $g'(\ln 3) \lt 0$를 만족시킨다.
또, 조건 (나)에서
$|\,g'(-\ln 3)\,| = \frac{3}{8}g(-\ln 3)$이고
$f'(\frac{1}{2}) \gt 0$이므로
$f'(\frac{1}{2}) \times \frac{3}{8} = \frac{3}{8} \times \{ -f(\frac{1}{2}) \}$
즉, $f'(\frac{1}{2}) = -f(\frac{1}{2})$
한편, $f'(1) = 0$이고 $f(x)$는 최고차항의 계수가 $1$인 삼차함수이므로
$f'(x) = 3(x -\,1)(x -\,a)$ ($a$는 $1$ 보다 큰 상수)로 놓을 수 있다.
이때, $f(x) = x^{3} -\,\frac{3(a + 1)}{2}x^{2} + 3ax + C$ ($C$는 적분상수)
라 하면
$f(\frac{1}{2}) = \frac{1}{8} -\,\frac{3(a + 1)}{8} + \frac{3a}{2} + C$
$= \frac{9}{8}a -\,\frac{1}{4} + C$
이므로
$\frac{3}{2}a -\,\frac{3}{4} = -\frac{9}{8}a + \frac{1}{4} -\,C$
즉, $C = -\frac{21}{8}a + 1$이므로
$f(x) = x^{3} -\,\frac{3(a + 1)}{2}x^{2} + 3ax -\,\frac{21}{8}a + 1$
그러므로
$g(0) = -f(1) = \frac{9}{8}a -\,\frac{1}{2}$
이때 $f(2) \le 0$이어야 하므로 $3 -\,\frac{21}{8}a \le 0$
즉, $a \ge \frac{8}{7}$이고
$g(0) \ge \frac{9}{8} \times \frac{8}{7} -\,\frac{1}{2} = \frac{11}{14}$이므로 $g(0)$의 최솟값은 $\dfrac{11}{14}$이다.
따라서 $p + q = 14 + 11 = 25$
수학 영역(기하)
25. 좌표평면 위의 두 점 $\mathrm{A}(4, 0)$, $\mathrm{B}(2, -4)$에 대하여 점 $\mathrm{A}$를 지나고 법선벡터가 $\overrightarrow{\mathrm{AB}}$인 직선의 $y\,$절편은? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
26. 쌍곡선 $\dfrac{x^2}{a^2} -\,\dfrac{y^2}{b^2} = 1$의 한 점근선의 방정식이 $y = \dfrac{1}{2}x$이다. 쌍곡선이 직선 $y = 1$과 만나는 두 점을 각각 $\mathrm{P}$, $\mathrm{Q}$라 하자. 쌍곡선 위의 점 $\mathrm{P}$에서의 접선과 쌍곡선 위의 점 $\mathrm{Q}$에서의 접선이 서로 수직일 때, $a^{2} + b^{2}$의 값은? (단, $a$, $b$는 양수이다.) [3점]
① $15$
② $\frac{35}{2}$
③ $20$
④ $\frac{45}{2}$
⑤ $25$
①
쌍곡선 $\frac{x^2}{a^2} -\,\frac{y^2}{b^2} = 1$의 점근선의 방정식이 $y = \frac{1}{2}x$이고, $a \gt 0$, $b \gt 0$이므로
$\frac{b}{a} = \frac{1}{2}$ 에서 $a = 2b$ $\cdots\cdots$ ㉠
그러므로 이 쌍곡선의 방정식은
$\frac{x^2}{4b^2} -\,\frac{y^2}{b^2} = 1$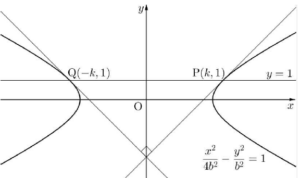
이 쌍곡선이 직선 $y = 1$과 만나는 점 중 제$\,1\,$사분면의 점을 $\mathrm{P}$, 제$\,2\,$사분면의 점을 $\mathrm{Q}$라 하고, 점 $\mathrm{P}$의 $x$좌표를 $k$ ($k \gt 0$)이라 하면 두 점 $\mathrm{P}$, $\mathrm{Q}$는 $y$축에 대하여 대칭이므로
$\mathrm{P}(k, 1)$, $\mathrm{Q}(-k, 1)$
두 점 $\mathrm{P}$, $\mathrm{Q}$가 쌍곡선 $\frac{x^2}{4b^2} -\,\frac{y^2}{b^2} = 1$ 위의 점이므로
$\frac{k^2}{4b^2} -\,\frac{1}{b^2} = 1$에서
$b^{2} = \frac{k^2}{4} -\,1$ $\cdots\cdots$ ㉡
쌍곡선 $\frac{x^2}{4b^2} -\,\frac{y^2}{b^2} = 1$ 위의 점 $\mathrm{P}(k, 1)$에서의 접선의 방정식은
$\frac{kx}{4b^2} -\,\frac{y}{b^2} = 1$, 즉 $y = \frac{k}{4}x -\,b^{2}$
쌍곡선 $\frac{x^2}{4b^2} -\,\frac{y^2}{b^2} = 1$ 위의 두 점 $\mathrm{P}$, $\mathrm{Q}$에서의 접선이 $y$축에 대하여 대칭이고 서로 수직이므로 점 $\mathrm{P}$에서의 접선의 기울기가 $1$이어야 한다. 즉, $\frac{k}{4} = 1$이므로 $k = 4$
㉡에서 $b^{2} = 4 -\,1 = 3$
㉠에서 $a^{2} = 4b^{2} = 4 \times 3 = 12$
따라서 $a^{2} + b^{2} = 15$
27. 삼각형 $\mathrm{OAB}$에 대하여 $\overrightarrow{\mathrm{OA}} = \vec{a}$, $\overrightarrow{\mathrm{OB}} = \vec{b}$라 하자. $$|\,\vec{a} + \vec{b}\,| = 6, \:|\,2\vec{a} -\,\vec{b}\,| = 9, \:(\vec{a} + \vec{b})\cdot(\vec{a} -\,\vec{b}) = 0$$ 일 때, 삼각형 $\mathrm{OAB}$의 넓이는? [3점]
① $4\sqrt{2}$
② $5\sqrt{2}$
③ $6\sqrt{2}$
④ $7\sqrt{2}$
⑤ $8\sqrt{2}$
③
$|\,\vec{a} + \vec{b}\,| = 6$의 양변을 제곱하여 정리하면
$|\,\vec{a} + \vec{b}\,|^{2} = (\vec{a} + \vec{b})\cdot(\vec{a} + \vec{b})$
$= |\,\vec{a}\,|^{2} + 2\vec{a}\cdot\vec{b} + |\,\vec{b}\,|^{2} = 36$ $\cdots\cdots$ ㉠
마찬가지로 $|\,2\vec{a} -\,\vec{b}\,| = 9$의 양변을 제곱하여 정리하면 $|\,2\vec{a} -\,\vec{b}\,|^{2} = 81$에서
$4|\,\vec{a}\,|^{2} -\,4\vec{a}\cdot\vec{b} + |\,\vec{b}\,|^{2} = 81$ $\cdots\cdots$ ㉡
한편, $(\vec{a} + \vec{b})\cdot(\vec{a} -\,\vec{b}) = 0$에서
$|\,\vec{a}\,|^{2} -\,|\,\vec{b}\,|^{2} = 0$, 즉 $|\,\vec{a}\,| = |\,\vec{b}\,|$ $\cdots\cdots$ ㉢
㉢을 ㉠, ㉡에 각각 대입하여 정리하면
$|\,\vec{a}\,|^{2} + \vec{a}\cdot\vec{b} = 18$ $\cdots\cdots$ ㉣
$5|\,\vec{a}\,|^{2} -\,4\vec{a}\cdot\vec{b} = 81$ $\cdots\cdots$ ㉤
$5 \times\,$㉣$\,-\,$㉤을 하면
$9\vec{a}\cdot\vec{b} = 9$, $\vec{a}\cdot\vec{b} = 1$ $\cdots\cdots$ ㉥
㉥을 ㉣에 대입하여 정리하면
$|\,\vec{a}\,|^{2} = 17$, $|\,\vec{a}\,| = |\,\vec{b}\,| = \sqrt{17}$
㉥에서 $|\,\vec{a}\,||\,\vec{b}\,|\cos (\angle \mathrm{AOB})= 1$
$\cos (\angle \mathrm{AOB}) = \frac{1}{17}$
$\sin (\angle \mathrm{AOB}) = \sqrt{1 -\,\cos^{2} (\angle \mathrm{AOB})}$ $= \sqrt{1 -\,(\frac{1}{17})^{2}}$ $= \dfrac{12\sqrt{2}}{17}$
따라서 삼각형 $\mathrm{OAB}$의 넓이는
$\dfrac{1}{2} \times |\,\vec{a}\,| \times |\,\vec{b}\,| \times \sin (\angle \mathrm{AOB})$
$= \dfrac{1}{2} \times (\sqrt{17})^{2} \times \dfrac{12\sqrt{2}}{17}$
$= 6\sqrt{2}$
$|\,\vec{a}\,| = |\,\vec{b}\,| = \sqrt{17}$이고 $\overline{\mathrm{OA}} = \overline{\mathrm{OB}} = \sqrt{17}$이므로 삼각형 $\mathrm{OAB}$는 이등변삼각형이다. 선분 $\mathrm{AB}$의 중점을 $\mathrm{M}$이라 하면 $\overline{\mathrm{OM}} \perp \overline{\mathrm{AB}}$이고 $|\,\vec{a} + \vec{b}\,| = 6$에서 $|\,\vec{a} + \vec{b}\,| = |\,2 \overrightarrow{\mathrm{OM}}\,| = 2 \overline{\mathrm{OM}} = 6$
$ \overline{\mathrm{OM}} = 3$
직각삼각형 $\mathrm{OAM}$에서
$\overline{\mathrm{AM}} = \sqrt{\overline{\mathrm{OA}}^{\,2} -\,\overline{\mathrm{OM}}^{\,2}}$
$= \sqrt{(\sqrt{17})^{2} -\,3^{,2}} = 2\sqrt{2}$
이므로 $\overline{\mathrm{AB}} = 2\overline{\mathrm{AM}} = 4\sqrt{2}$
따라서 삼각형 $\mathrm{OAB}$의 넓이는
$\dfrac{1}{2} \times \overline{\mathrm{AB}} \times \overline{\mathrm{OM}}$
$= \dfrac{1}{2} \times 4\sqrt{2} \times 3$
$= 6\sqrt{2}$
28. 그림과 같이 두 점 $\mathrm{F}(c, 0)$, $\mathrm{F}'(-c, 0)$ ($c \gt 0$)을 초점으로 하는 타원 $C_{1} : \dfrac{x^2}{a^2} + y^{2} = 1$과 두 점 $\mathrm{G}(0, d)$, $\mathrm{G}'(0, -d)$ ($d \gt 1$)을 초점으로 하고 타원 $C_{1}$의 두 꼭짓점을 지나는 타원 $C_{2}$가 있다. 직선 $\mathrm{FG}$가 타원 $C_{1}$과 제$\,1\,$사분면에서 만나는 점을 $\mathrm{P}$ 라 하고, 직선 $\mathrm{F'P}$가 타원 $C_{2}$와 제$\,1\,$사분면에서 만나는 점을 $\mathrm{Q}$라 하자. $\overline{\mathrm{GP}} = \overline{\mathrm{PF}}$이고 $\overline{\mathrm{GP}} + \overline{\mathrm{PF}'} = 2\sqrt{2}$일 때, $\overline{\mathrm{QG}} + \overline{\mathrm{QG}'}$의 값은? (단, $a$는 양수이다.) [4점]
① $\sqrt{19}$
② $2\sqrt{5}$
③ $\sqrt{21}$
④ $\sqrt{22}$
⑤ $\sqrt{23}$
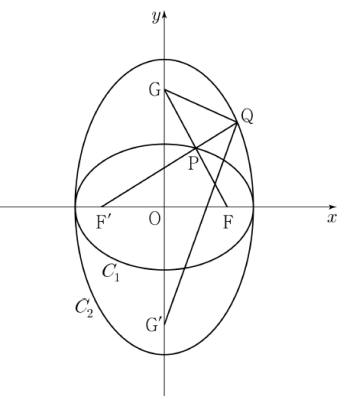
④
타원 $C_{1} : \frac{x^2}{a^2} + y^{2} = 1$의 장축의 길이가 $2a$이고, $\overline{\mathrm{GP}} = \overline{\mathrm{PF}}$이므로
$\overline{\mathrm{GP}} + \overline{\mathrm{PF’}} = \overline{\mathrm{PF}} + \overline{\mathrm{PF’}} = 2a$
즉, $2a – = 2\sqrt{2}$에서 $a = \sqrt{2}$
이때 $c^{2} = a^{2} -\,1$에서 $c = 1$이므로
$\mathrm{F}(1, 0)$, $\mathrm{F’}(-1, 0)$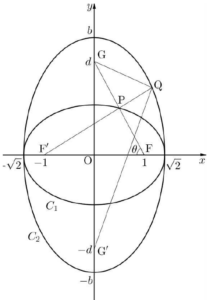
$\overline{\mathrm{PF}} = k$ ($k \gt 0$)이라 하면 $\overline{\mathrm{GF}} = 2k$이고, $\overline{\mathrm{PF’}} = 2\sqrt{2} -\,\overline{\mathrm{PF}} = 2\sqrt{2} -\,k$
$\angle \mathrm{PFF’} = \theta$라 하면 직각삼각형 $\mathrm{GOF}$에서
$\cos \theta = \dfrac{\overline{\mathrm{OF}}}{\overline{\mathrm{GF}}}$
$\cdots\cdots$ ㉠
삼각형 $\mathrm{PF’F}$에서 코사인법칙에 의해
$\cos \theta = \dfrac{\overline{\mathrm{PF}}^{2} + \overline{\mathrm{F’F}}^{2} -\,\overline{\mathrm{PF’}}^{2}}{2 \times \overline{\mathrm{PF}} \times \overline{\mathrm{F’F}}}$
$= \dfrac{k^{2} + 4 -\,(2\sqrt{2} -\,k)^{2}}{2 \times 2 \times k}$
$= \dfrac{4k\sqrt{2} -\,4}{4k}$
$= \dfrac{k\sqrt{2} -\,1}{k}$ $\cdots\cdots$ ㉡
㉠, ㉡에서 $\frac{1}{2k} = \frac{k\sqrt{2} -\,1}{k}$
$2k\sqrt{2} = 3$, $k = \dfrac{3\sqrt{2}}{4}$
그러므로 직각삼각형 $\mathrm{GOF}$에서
$\overline{\mathrm{OG}}^{\,2} = \overline{\mathrm{GF}}^{\,2} -\,\overline{\mathrm{OF}}^{\,2}$이므로
$d^{2} = 4k^{2} -\,1 = 4 \times \frac{9}{8} -\,1 = \frac{7}{2}$
타원 $C_2$의 꼭짓점 중 $y$좌표가 양수인 점의 $y$좌표를 $b$라 하면
$b^{2} -\,(\sqrt{2})^{2} = \frac{7}{2}$
이므로
$b^{2} = \frac{11}{2}$
이때 $b \gt 0$이므로 $b = \frac{\sqrt{22}}{2}$
따라서 $\overline{\mathrm{QG}} + \overline{\mathrm{QG}’}$의 값은 타원 의 장축의 길이이므로
$\overline{\mathrm{QG}} + \overline{\mathrm{QG}’} = 2b = 2 \times \frac{\sqrt{22}}{2} = \sqrt{22}$
29. 그림과 같이 두 점 $\mathrm{F}(c, 0)$, $\mathrm{F}'(-c, 0)$ ($c \gt 0$)을 초점으로 하는 쌍곡선이 있다. 이 쌍곡선 위의 점 중 제$\,1\,$사분면에 있는 점 $\mathrm{P}$에 대하여 선분 $\mathrm{F'P}$가 $y\,$축과 만나는 점을 $\mathrm{Q}$라 하고, 원점 $\mathrm{O}$를 지나고 선분 $\mathrm{F'P}$와 평행한 직선이 이 쌍곡선과 만나는 점 중 제$\,1\,$사분면에 있는 점을 $\mathrm{R}$이라 하자. $\overline{\mathrm{F'Q}} = \overline{\mathrm{QP}}$, $\overline{\mathrm{OQ}} = 2$이고 삼각형 $\mathrm{PQR}$의 넓이가 $3$일 때, 이 쌍곡선의 주축의 길이는 $p + q\sqrt{13}$이다. $p^{2} + q^{2}$의 값을 구하시오. (단, $p$와 $q$는 유리수이다.) [4점]
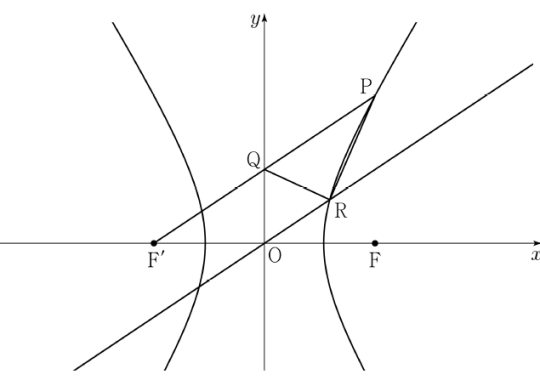
$20$
주어진 쌍곡선은 $y$축에 대하여 대칭이므로
$\overline{\mathrm{F’Q}} = \overline{\mathrm{QP}} = \overline{\mathrm{QF}}$
즉, 점 $\mathrm{Q}$는 세 점 $\mathrm{P}$, $\mathrm{F’}$, $\mathrm{f}$를 지나는 원의 중심이고 이때 선분 $\mathrm{PF’}$이 이 원의
지름이므로
$\angle \mathrm{PFF’} = \frac{\pi}{2}$
또, 삼각형 $\mathrm{QF’O}$와 삼각형 $\mathrm{PF’F}$가 서로 닮음이고 그 닮음비가 $1 : 2$이므로 $\overline{\mathrm{PF}} = 2 \times \overline{\mathrm{OQ}} = 4$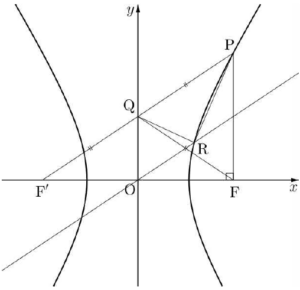 
한편, 직선 $\mathrm{F’P}$와 직선 $\mathrm{OR}$이 서로 평행하며 $\overline{\mathrm{F’Q}} = \overline{\mathrm{QP}}$이고, 삼각형 $\mathrm{PQR}$의 넓이가 $3$이므로 삼각형 $\mathrm{QF’O}$의 넓이도 $3$이다.
즉, $\dfrac{1}{2} \times \overline{\mathrm{OF’}} \times \overline{\mathrm{OQ}} = 3$에서
$\dfrac{1}{2} \times \overline{\mathrm{OF’}} \times 2 = 3$, $\overline{\mathrm{OF’}} = 3$
그러므로 $\overline{\mathrm{F’Q}}^{\,2} = \overline{\mathrm{OF’}}^{\,2} + \overline{\mathrm{OQ}}^{\,2}$ $= 3^{2} + 2^{2} = 13$
즉, $\overline{\mathrm{F’Q}} = \overline{\mathrm{QP}} = \sqrt{13}$
이때 $\overline{\mathrm{PF’Q}} -\,\overline{\mathrm{PF}} = 2\sqrt{13} -\,4$이므로 이 쌍곡선의 주축의 길이는 $2\sqrt{13} -\,4$이다.
따라서 $p = -4$, $q = 2$이므로
$p^{2} + q^{2} = 16 + 4 = 20$
30. 좌표평면에 $\overline{\mathrm{AB}} = 6$, $\overline{\mathrm{AD}} = 8$인 직사각형 $\mathrm{ABCD}$와 $2\overrightarrow{\mathrm{BE}} = 3\overrightarrow{\mathrm{BC}} -\,\overrightarrow{\mathrm{BA}}$를 만족시키는 점 $\mathrm{E}$가 있다. 선분 $\mathrm{BC}$ 위를 움직이는 점 $\mathrm{P}$에 대하여 점 $\mathrm{Q}$가 $$\overrightarrow{\mathrm{PQ}}\cdot(\overrightarrow{\mathrm{PQ}} -\,\overrightarrow{\mathrm{AB}}) = 0$$을 만족시킬 때, $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 최솟값을 구하시오. [4점]
$36$
$2\overrightarrow{\mathrm{BE}} = 3\overrightarrow{\mathrm{BC}} -\,\overrightarrow{\mathrm{BA}}$에서
$\overrightarrow{\mathrm{BE}} = \dfrac{3\overrightarrow{\mathrm{BC}} -\,\overrightarrow{\mathrm{BA}}}{3 -\,1}$
이므로 점 $\mathrm{E}$는 선분 $\mathrm{AC}$를 $3 : 1$로 외분하는 점이다.
선분 $\mathrm{BC}$ 위를 움직이는 점 $\mathrm{P}$에 대하여 점 $\mathrm{P}’$을
$\overrightarrow{\mathrm{BP’}} = \overrightarrow{\mathrm{BP}} + \overrightarrow{\mathrm{AB}}$가 되도록 잡으면
$\overrightarrow{\mathrm{PQ}} -\,\overrightarrow{\mathrm{AB}}$
$=\overrightarrow{\mathrm{BQ}} -\,\overrightarrow{\mathrm{BP}} -\,\overrightarrow{\mathrm{AB}}$
$=\overrightarrow{\mathrm{BQ}} -\,(\overrightarrow{\mathrm{BP’}} -\,\overrightarrow{\mathrm{AB}}) -\,\overrightarrow{\mathrm{AB}}$
$=\overrightarrow{\mathrm{BQ}} -\,\overrightarrow{\mathrm{BP’}}$
$=\overrightarrow{\mathrm{P’Q}}$
이고
$\overrightarrow{\mathrm{PQ}}\cdot(\overrightarrow{\mathrm{PQ}} -\,\overrightarrow{\mathrm{AB}}) = 0$에서 $\overrightarrow{\mathrm{PQ}}\cdot\overrightarrow{\mathrm{P’Q}} = 0$
즉, 점 $\mathrm{Q}$는 선분 $\mathrm{PP’}$을 지름으로 하는 원 위의 점이다.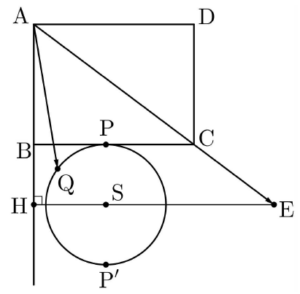
점 $\mathrm{Q}$가 나타내는 원의 중심을 $\mathrm{S}$, 점 $\mathrm{S}$에서 직선 $\mathrm{AB}$에 내린 수선의 발을 $\mathrm{H}$하면 점 $\mathrm{E}$는 직선 $\mathrm{SH}$ 위의 점이다.
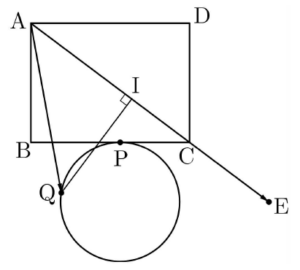
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$
$= \overrightarrow{\mathrm{AE}}\cdot(\overrightarrow{\mathrm{AH}} + \overrightarrow{\mathrm{HS}} + \overrightarrow{\mathrm{SQ}})$
$= \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AH}} + \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{HS}} + \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{SQ}}$
이고,
$0 \le t \le 8$인 실수 $t$에 대하여 $\overrightarrow{\mathrm{HS}} = t\overrightarrow{\mathrm{BC}}$
이므로 $t = 0$이고 두 벡터 $\overrightarrow{\mathrm{SQ}}$, $\overrightarrow{\mathrm{AE}}$의 방향이 서로 반대일 때 $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 값은 최소이다. 즉, $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 최솟값은
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$
$= \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AH}} + 0 + \overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{SQ}}$
$= |\,\overrightarrow{\mathrm{AH}}\,|^{2} -\,|\,\overrightarrow{\mathrm{AE}}\,||\,\overrightarrow{\mathrm{SQ}}\,|$
$= 9^{2} -\,\sqrt{9^{2} + 12^{2}} \times 3$
$= 81 -\,15 \times 3$
$= 36$
점 $\mathrm{Q}$에서 직선 $\mathrm{AE}$에 내린 수선의 발을 $\mathrm{I}$라 하면 점 $\mathrm{I}$는 점 $\mathrm{P}$의 위치에 관계없이 선분 $\mathrm{AB}$ 위에 있고
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}} = |\,\overrightarrow{\mathrm{AE}}\,||\,\overrightarrow{\mathrm{AQ}}\,| \cos (\angle \mathrm{QAE})$
$= \overline{\mathrm{AE}} \times \overline{\mathrm{AI}}$
이다. 이때
$\overline{\mathrm{AE}} = \frac{3}{2}\overline{\mathrm{AC}}$ $= \frac{3}{2} \sqrt{\overline{\mathrm{AB}}^{\,2} + \overline{\mathrm{BC}}^{\,2}}$
$= \frac{3}{2} \times \sqrt{6^{2} + 8^{2}} = \frac{3}{2} \times 10 = 15$
이고 선분 $\mathrm{AI}$의 길이는 점 $\mathrm{P}$가 점 $\mathrm{B}$와 일치하고 직선 $\mathrm{QI}$가 점 $\mathrm{Q}$가 나타내는 원에 접할 때 최소이다.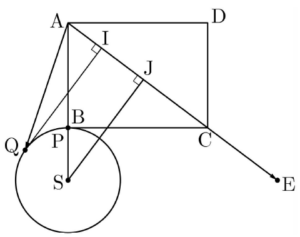 
점 $\mathrm{Q}$가 나타내는 원의 중심을 $\mathrm{S}$라 하고 점 $\mathrm{S}$에서 직선 $\mathrm{AE}$에 내린 수선의 발을 $\mathrm{J}$라 하면
$\overline{\mathrm{AJ}} = \overline{\mathrm{AS}} \cos (\angle \mathrm{SAJ})$ $= 9 \times \frac{3}{5} = \frac{27}{5}$
$\overline{\mathrm{AI}} = \overline{\mathrm{AJ}} -\,\overline{\mathrm{IJ}}$ $= \frac{27}{5} -\,3 = \frac{12}{5}$
따라서 $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 최솟값은
$\overline{\mathrm{AE}} \times \overline{\mathrm{AI}} = 15 \times \frac{12}{5} = 36$
네 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$, $\mathrm{D}$의 좌표를 각각 $(0, 6)$, $(0, 0)$, $(8, 0)$, $(8, 6)$이라 하자.
$2\overrightarrow{\mathrm{BE}} = 3\overrightarrow{\mathrm{BC}} -\,\overrightarrow{\mathrm{BA}}$에서
$\overrightarrow{\mathrm{BE}} = \dfrac{3\overrightarrow{\mathrm{BC}} -\,\overrightarrow{\mathrm{BA}}}{2}$
$= \dfrac{3(8, 0) -\,(0, 6)}{2}$
$= (12, -3)$
이다. 점 $\mathrm{P}$가 선분 $\mathrm{BC}$ 위를 움직이는 점이므로 $0 \le t \le 8$인 실수 $t$에 대하여 점 $\mathrm{P}$의 좌표를 $(t, 0)$으로 놓을 수 있다.
점 $\mathrm{Q}$의 좌표를 $(x, y)$라 하면
$\overrightarrow{\mathrm{PQ}}\cdot(\overrightarrow{\mathrm{PQ}} -\,\overrightarrow{\mathrm{AB}}) = 0$에서
$(x -\,t, y)\cdot( (x -\,t, y) -\,(0, -6) )$
$= (x -\,t, y)\cdot(x -\,t, y + 6)$
$= (x -\,t)^{2} + y(y + 6) = 0$
$(x -\,t)^{2} + (y + 3)^{2} = 3^{2}$
즉, 점 $\mathrm{Q}$는 점 $(t, -3)$을 중심으로 하고 반지름의 길이가 $3$인 원 위의 점이다.
이때 $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}} = k$라 하면
$\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$
$= ( (12, -3) -\,(0, 6) )\cdot( (x, y) -\,(0, 6) )$
$= (12, -9)\cdot(x, y -\,6)$
$= 12x -\,9(y -\,6)$
$= 12x -\,9y + 54 = k$
$12x -\,9y + 54 -\,k = 0$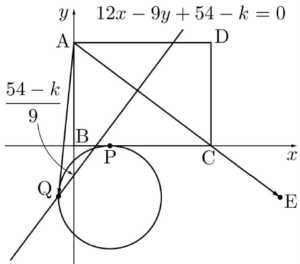
즉, $\overrightarrow{\mathrm{AE}}\cdot\overrightarrow{\mathrm{AQ}}$의 값은 기울기가 $\frac{4}{3}$이고 점 $\mathrm{Q}$를 지나는 직선의 $y$절편이 최대일 때 최소이다. 
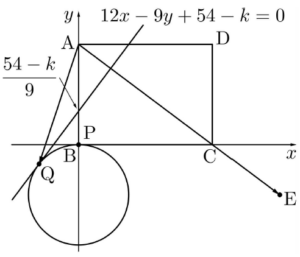따라서 $t = 0$일 때, 즉, 원 $x^{2} + (y + 3)^{2} = 3^{2}$에 접하고 기울기가 $\frac{4}{3}$인 직선의 $y$절편이 최대일 때 $k$의 값이 최소이므로 $k$의 최솟값을 $k_{0}$이라 하면
$\dfrac{|\,-9 \times (-3) + 54 -\,k_{0}\,|}{\sqrt{12^{2} + (-9)^{2}}} = 3$에서
$81 -\,k_{0} = 45$
$k_{0} = 81 -\,45 = 36$