25년 11월 대수능
1. $9^{\frac{1}{4}}\times 3^{-\frac{1}{2}}$의 값은? [2점]
① $1$
② $\sqrt{3}$
③ $3$
④ $3\sqrt{3}$
⑤ $9$
3. 수열 $\{ a_n \}$에 대하여 $\displaystyle \sum_{k=1}^{4}(2a_{k}-k) = 0$일 때, $\displaystyle \sum_{k=1}^{4}a_{k}$의 값은? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
4. 함수 $$f(x) = \begin{cases} 3x-2 & (x \lt 1) \\ x^{2}-3x+a & (x \ge 1) \end{cases}$$ 이 실수 전체의 집합에서 연속일 때, 상수 $a$의 값은? [3점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
③
함수 $f(x)$가 실수 전체의 집합에서 연속이므로 $x=1$에서도 연속이어야 한다.
즉, $\displaystyle \lim_{x \to 1-}f(x) = \lim_{x \to 1+}f(x) = f(1)$ 이어야 한다.
이때,
$\displaystyle \lim_{x \to 1-}f(x) = \lim_{x \to 1-}(3x-2) = 3\times 1-2 = 1$
$\displaystyle \lim_{x \to 1+}f(x) = \lim_{x \to 1+}(x^{2}-3x+a) = 1^{2}-3\times 1 + a = -2+a$
$f(1) = 1^{2}-3\times 1 + a = -2+a$
이므로
$1 = -2+a$
따라서 $a = 3$
6. $1$ 보다 큰 두 실수 $a$, $b$가 $$\log_{a}b = 3, \:\log_{3}\frac{b}{a} = \frac{1}{2}$$ 을 만족시킬 때, $\log_{9}ab$의 값은? [3점]
① $\frac{3}{8}$
② $\frac{1}{2}$
③ $\frac{5}{8}$
④ $\frac{3}{4}$
⑤ $\frac{7}{8}$
②
로그의 정의에 의하여
$\log_{a}b = 3$에서 $b = a^{3}$
이때
$\log_{3}\frac{b}{a} = \log_{3}\frac{a^3}{a} = \log_{3}a^{2} = 2\log_{3}a = \frac{1}{2}$
에서
$\log_{3}a = \frac{1}{4}$
이므로
$\log_{3}b = 3\log_{3}a = \frac{3}{4}$
따라서 로그의 성질에 의해
$\log_{9}ab = \log_{3^{2}}(a\times a^{3})$
$= \frac{4}{2}\log_{3}a = 2\times \frac{1}{4} = \frac{1}{2}$
7. 두 곡선 $y = x^{2}+3$, $y = -\dfrac{1}{5}x^{2}+3$과 직선 $x = 2$로 둘러싸인 부분의 넓이는? [3점]
① $\frac{18}{5}$
② $\frac{7}{2}$
③ $\frac{17}{5}$
④ $\frac{33}{10}$
⑤ $\frac{16}{5}$
8. $\sin \theta + 3 \cos \theta = 0$이고 $\cos (\pi-\theta) \gt 0$일 때, $\sin \theta$의 값은? [3점]
① $\frac{3\sqrt{10}}{10}$
② $\frac{\sqrt{10}}{5}$
③ $0$
④ $-\frac{\sqrt{10}}{5}$
⑤ $-\frac{3\sqrt{10}}{10}$
①
$\cos (\pi-\theta) = -\cos \theta \gt 0$이므로 $\cos \theta \lt 0$
이때, $\sin \theta + 3 \cos \theta = 0$에서
$\sin \theta = -3 \cos \theta \gt 0$이고,
$\sin^{2}\theta = 9 \cos^{2}\theta$
$= 9(1-\sin^{2}\theta)$ $= 9-9\sin^{2}\theta$
$10\sin^{2}\theta = 9$
$\sin^{2}\theta = \frac{9}{10}$
$\sin \theta \gt 0$이므로
$\sin \theta = \frac{3}{\sqrt{10}} = \dfrac{3\sqrt{10}}{10}$
9. 양수 $a$에 대하여 함수 $f(x)$를 $$f(x) = x^{3}+3ax^{2}-9a^{2}x+4$$ 라 하자. 직선 $y = 5$가 곡선 $y = f(x)$에 접할 때, $f(2)$의 값은? [4점]
① $11$
② $12$
③ $13$
④ $14$
⑤ $15$
④
$f'(x) = 3x^{2}+6ax-9a^{2}$ $= 3(x+3a)(x-a)$
$f'(x) = 0$에서
$x = -3a$ 또는 $x = a$
$a \gt 0$이므로 함수 $f(x)$의 증가와 감소를 표로 나타내면 다음과 같다.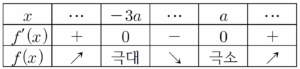 
한편, $f(0) = 4 \lt 5$이고, 직선 $y = 5$가 곡선 $y = f(x)$에 접하므로
$f(-3a) = 5$이어야 한다.
$f(-3a) = (-3a)^{3}+3a(-3a)^{2}-9a^{2}(-3a)+4$ $= 27a^{3}+4$
이므로
$27a^{3}+4 = 5$에서 $a^{3} = \frac{1}{27}$
$a$가 양수이므로 $a = \frac{1}{3}$
따라서 $f(x) = x^{3}+x^{2}-x+4$이므로
$f(2) = 2^{3}+2^{2}-2+4$ $= 14$
10. 상수 $a$ ($a \gt 1$)에 대하여 곡선 $y = a^{x}-2$ 위의 점 중 제$1$사분면에 있는 점 $\mathrm{A}$를 지나고 $y$축에 평행한 직선이 $x$축과 만나는 점을 $\mathrm{B}$, 곡선 $y = a^{x}-2$의 점근선과 만나는 점을 $\mathrm{C}$라 하자. $\overline{\mathrm{AB}} = \overline{\mathrm{BC}}$이고 삼각형 $\mathrm{AOC}$의 넓이가 $8$일 때, $a\times \overline{\mathrm{OB}}$의 값은? (단, $\mathrm{O}$는 원점이다.) [4점]
① $2^{\frac{13}{6}}$
② $2^{\frac{7}{3}}$
③ $2^{\frac{5}{2}}$
④ $2^{\frac{8}{3}}$
⑤ $2^{\frac{17}{6}}$
③
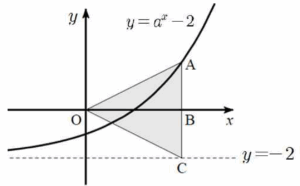$a \gt 1$이므로 함수 $y = a^{x}-2$의 그래프는 위 그림과 같고 이 곡선의 점근선은 직
선 $y = -2$이다.
점 $\mathrm{A}$의 좌표를 $(p, q)$라 하면
$\overline{\mathrm{AB}} = \overline{\mathrm{BC}} = 2$
이므로
$q = 2$
점 $\mathrm{A}$는 곡선 $y = a^{x}-2$ 위의 점이므로
$2 = a^{p}-2$
즉, $a^{p} = 4$에서 $p = \log_{a}4$
이때 삼각형 $\mathrm{AOC}$의 넓이가 $8$이므로
$\frac{1}{2}\times \overline{\mathrm{AC}}\times \overline{\mathrm{OB}} = 8$에서
$\overline{\mathrm{OB}} = 4$
즉, $\log_{a}4 = 4$이므로 $a^{4} = 4$
$a \gt 1$이므로 $a = \sqrt{2}$
따라서 $a\times \overline{\mathrm{OB}}$ $= \sqrt{2}\times 4 = 2^{\frac{1}{2}+2}$ $= 2^{\frac{5}{2}}$
11. 시각 $t = 0$일 때 원점을 출발하여 수직선 위를 움직이는 점 $\mathrm{P}$가 있다. 실수 $k$에 대하여 시각이 $t$ ($t \ge 0$)일 때 점 $\mathrm{P}$의 속도 $v(t)$가 $$v(t) = t^{2}-kt+4$$ 이다. <보기>에서 옳은 것만을 있는 대로 고른 것은? [4점]
ㄱ. $k = 0$이면, 시각 $t = 1$일 때 점 $\mathrm{P}$의 위치는 $\frac{13}{3}$이다.
ㄴ. $k = 3$이면, 출발한 후 점 $\mathrm{P}$의 운동 방향이 한 번 바뀐다.
ㄷ. $k = 5$이면, 시각 $t = 0$에서 $t = 2$ 까지 점 $\mathrm{P}$가 움직인 거리는 $3$이다.
① ㄱ
② ㄱ, ㄴ
③ ㄱ, ㄷ
④ ㄴ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
③
ㄱ.
$k = 0$이면 $v(t) = t^{2}+4$이므로 $t = 1$일 때 점 $\mathrm{P}$의 위치는
$0 + \int_{0}^{1}(t^{2}+4)dt$
$= \bigg[ \frac{1}{3}t^{3}+4t \bigg]_{0}^{1}$
$= \frac{1}{3}+4-0$
$= \dfrac{13}{3}$ (참)
ㄴ.
$k = 3$이면 $v(t) = t^{2}-3t+4$이므로 $v(t) = (t-\frac{3}{2})^{2}+\frac{7}{4} \gt 0$
따라서 출발한 후 점 $\mathrm{P}$의 운동 방향은 바뀌지 않는다. (거짓)
ㄷ.
$k = 5$이면 $v(t) = t^{2}-5t+4$이므로 $v(t) = (t-1)(t-4)$
$0 \lt t \lt 1$일 때, $v(t) \gt 0$이고
$1 \lt t \lt 2$일 때, $v(t) \lt 0$이므로
시각 $t = 0$에서 시각 $t = 2$ 까지 점 $\mathrm{P}$가 움직인 거리를 $s$라 하면
$s = \int_{0}^{2}|v(t)| dt$
$= \int_{0}^{2}|t^{2}-5t+4| dt$
$= \int_{0}^{1}(t^{2}-5t+4) dt + \int_{1}^{2}\{-(t^{2}-5t+4)\} dt$
$= \bigg[ \frac{1}{3}t^{3}-\frac{5}{2}t^{2}+4t \bigg]_{0}^{1}-\bigg[ \frac{1}{3}t^{3}-\frac{5}{2}t^{2}+4t \bigg]_{1}^{2}$
$= \frac{1}{3}-\frac{5}{2}+4-\{ (\frac{8}{3}-10+8)-(\frac{1}{3}-\frac{5}{2}+4) \}$
$= 3$ (참)
이상에서 옳은 것은 ㄱ, ㄷ이다.
12. 등비수열 $\{ a_n \}$이 $$2(a_{1}+a_{4}+a_{7}) = a_{4}+a_{7}+a_{10} = 6$$ 을 만족시킬 때, $a_{10}$의 값은? [4점]
① $\frac{22}{7}$
② $\frac{24}{7}$
③ $\frac{26}{7}$
④ $\frac{30}{7}$
⑤ $\frac{32}{7}$
②
등비수열 $\{ a_{n} \}$의 공비를 $r$이라 하자.
$2(a_{1}+a_{4}+a_{7}) = 6$에서 $2(a_{1}+a_{1}r^{3}+a_{1}r^{6}) = 2a_{1}(1+r^{3}+r^{6}) = 6$
$a_{1}(1+r^{3}+r^{6}) = 3$ $\cdots\cdots$ ㉠
$a_{4}+a_{7}+a_{10} = 6$에서
$a_{1}r^{3}+a_{1}r^{6}+a_{1}r^{9}$
$= a_{1}r^{3}(1+r^{3}+r^{6}) = 6$ $\cdots\cdots$ ㉡
㉡$\,\div\,$㉠을 하면 $r^{3} = 2$
㉠에 $r^{3} = 2$를 대입하면 $a_{1}(1+2+2^{2}) = 3$
$a_{1} = \frac{3}{7}$
따라서 $a_{10} = a_{1}r^{9}= \frac{3}{7}\times 2^{3} = \dfrac{24}{7}$
13. 함수 $f(x) = x^{2}-4x-3$에 대하여 곡선 $y = f(x)$ 위의 점 $(1, -6)$에서의 접선을 $l$이라 하고, 함수 $g(x) = (x^{3}-2x)f(x)$에 대하여 곡선 $y = g(x)$ 위의 점 $(1, \,6)$에서의 접선을 $m$이라 하자. 두 직선 $l$, $m$과 $y$축으로 둘러싸인 도형의 넓이는? [4점]
① $21$
② $28$
③ $35$
④ $42$
⑤ $49$
⑤
$f'(x) = 2x-4$에서 $f'(1) = -2$이므로 곡선 $y = f(x)$ 위의 점 $(1, -6)$에서의 접선 $l$의 방정식은
$y = -2(x-1)-6$ 즉, $y = -2x-4$
$g(x) = (x^{3}-2x)f(x)$에서 곱의 미분법에 의하여
$g'(x) = (3x^{2}-2)f(x)+(x^{3}-2x)f'(x)$
이므로
$g'(1) = (3-2)f(1)+(1-2)f'(1)$ $ = 1\times (-6)+(-1)\times (-2) = -4$
곡선 $y = g(x)$ 위의 점 $(1, 6)$에서의 접선 $m$의 방정식은
$y = -4(x-1)+6$ 즉, $y = -4x+10$
이때 두 직선 $y = -2x-4$, $y = -4x+10$의 교점의 $x$좌표는
$-2x-4 = -4x+10$에서 $x = 7$이므로 두 직선과 $y$축으로 둘러싸인 도형의 넓이는
$\frac{1}{2}\times \{ 10-(-4) \}\times 7 = 49$
14. 그림과 같이 $\overline{\mathrm{AB}} = 3$, $\overline{\mathrm{BC}} = 4$이고 $\angle \mathrm{B} = \dfrac{\pi}{2}$인 직각삼각형 $\mathrm{ABC}$가 있다. 선분 $\mathrm{AB}$를 $2 : 1$로 내분하는 점을 $\mathrm{D}$, 점 $\mathrm{A}$를 중심으로 하고 반지름의 길이가 $\overline{\mathrm{AD}}$인 원이 선분 $\mathrm{AC}$와 만나는 점을 $\mathrm{E}$, 직선 $\mathrm{AB}$가 이 원과 만나는 점 중 $\mathrm{D}$가 아닌 점을 $\mathrm{F}$라 하고, 호 $\mathrm{EF}$ 위의 점 $\mathrm{G}$를 $\overline{\mathrm{CG}} = 2\sqrt{6}$이 되도록 잡는다. 세 점 $\mathrm{C}$, $\mathrm{E}$, $\mathrm{G}$를 지나는 원 위의 점 $\mathrm{H}$가 $\angle \mathrm{HCG} = \angle \mathrm{BAC}$를 만족시킬 때, 선분 $\mathrm{GH}$의 길이는? [4점]
① $\frac{6\sqrt{15}}{5}$
② $\frac{38\sqrt{10}}{25}$
③ $\frac{14\sqrt{3}}{5}$
④ $\frac{32\sqrt{15}}{25}$
⑤ $\frac{8\sqrt{10}}{5}$
④
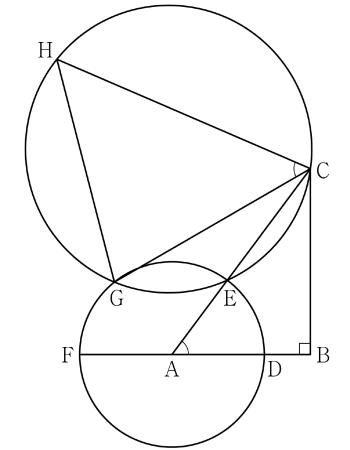
$\angle \mathrm{HCG} = \angle \mathrm{BAC} = \theta_{1}$이라 하자.
직각삼각형 $\mathrm{ABC}$에서
$\overline{\mathrm{AC}}^{2} = \sqrt{(\overline{\mathrm{AB}})^{2}+(\overline{\mathrm{BC}})^{2}}$ $= \sqrt{3^{2}+4^{2}} = 5$
이므로
$\sin \theta_{1} = \frac{4}{5}$
또한 $\overline{\mathrm{AD}} = \overline{\mathrm{AE}} = \overline{\mathrm{AG}} = 2$이므로
$\angle \mathrm{CAG} = \theta_{2}$라 하면 삼각형 $\mathrm{ACG}$에서 코사인법칙에 의하여
$\cos \theta_{2} = \dfrac{(\overline{\mathrm{AG}})^{2}+(\overline{\mathrm{AC}})^{2}-(\overline{\mathrm{CG}})^{2}}{2 \times \overline{\mathrm{AG}}\times \overline{\mathrm{AC}}}$
$= \dfrac{2^{2}+5^{2}-(2\sqrt{6})^{2}}{2\times 2 \times 5} = \dfrac{1}{4}$
따라서 삼각형 $\mathrm{AEG}$에서 코사인법칙에 의하여
$\overline{\mathrm{GE}}^{2} = (\overline{\mathrm{AG}})^{2}+(\overline{\mathrm{AE}})^{2}-2\times \overline{\mathrm{AG}}\times \overline{\mathrm{AE}}\times \cos \theta_{2}$
$= 2^{2}+2^{2}-2\times 2\times 2\times \frac{1}{4} = 6$
$\therefore$ $\overline{\mathrm{GE}} = \sqrt{6}$
삼각형 $\mathrm{CGE}$에서 $\angle \mathrm{ECG} = \theta_{3}$이라 하면
코사인법칙에 의하여
$\cos \theta_{3} = \dfrac{(\overline{\mathrm{CG}})^{2}+(\overline{\mathrm{CE}})^{2}-(\overline{\mathrm{GE}})^{2}}{2 \times \overline{\mathrm{CG}}\times \overline{\mathrm{CE}}}$
$= \dfrac{(2\sqrt{6})^{2}+3^{2}-(\sqrt{6})^{2}}{2\times (2\sqrt{6}) \times 3} = \dfrac{3\sqrt{6}}{8}$
따라서
$\sin \theta_{3} = \sqrt{1-(\frac{3\sqrt{6}}{8})^{2}} = \frac{\sqrt{10}}{8}$
삼각형 $\mathrm{CGE}$의 외접원의 반지름의 길이를 $R$이라 하면 사인법칙에 의하여
$2R = \dfrac{\overline{\mathrm{GE}}}{\sin \theta_3}$
$= \dfrac{\sqrt{6}}{\frac{\sqrt{10}}{8}} = \dfrac{8\sqrt{15}}{5}$
따라서 삼각형 $\mathrm{CHG}$에서 사인법칙에 의하여
$\overline{\mathrm{GH}} = 2R \times \sin \theta_1$
$ = \dfrac{8\sqrt{15}}{5}\times \dfrac{4}{5}$ $ = \dfrac{32\sqrt{15}}{25}$
15. 함수 $f(x)$가 $$f(x) = \begin{cases} -x^{2} & (x \lt 0) \\ \\ x^{2}-x & (x \ge 0) \end{cases}$$ 이고, 양수 $a$에 대하여 함수 $g(x)$를 $$g(x) = \begin{cases} ax+a & (x \lt -1) \\ \\ \: 0 & (-1 \le x \lt 1) \\ \\ ax-a & (x \ge 1) \end{cases}$$ 이라 하자. 함수 $h(x) = \displaystyle \int_{0}^{x}(g(t)-f(t))dt$가 오직 하나의 극값을 갖도록 하는 $a$의 최댓값을 $k$라 하자. $a = k$일 때, $k+h(3)$의 값은? [4점]
① $\frac{9}{2}$
② $\frac{11}{2}$
③ $\frac{13}{2}$
④ $\frac{15}{2}$
⑤ $\frac{17}{2}$
④
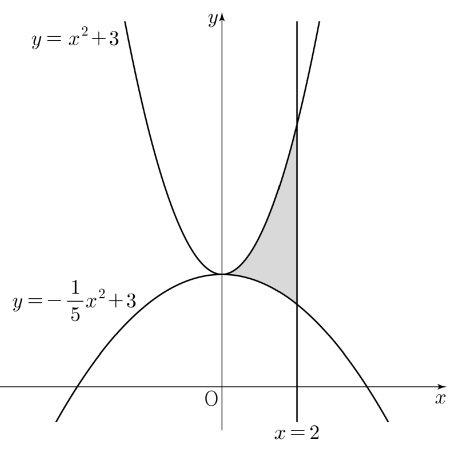
$h(x) = \int_{0}^{x}(g(t)-f(t))dt$에서 $h'(x) = g(x)-f(x)$이므로 함수 $h(x)$가 오직 하나의 극값을 가지려면
$h'(x) = 0$, 즉 $f(x) = g(x)$이면서 $h'(x) = 0$인 점의 좌우에서 $h'(x)$의 부호가 바뀌는 점이 오직 한 개만 있어야 한다.
이때 $f'(1) = 1$이므로 $a \le 1$이면 다음 그림과 같이 $x=0$ 또는 $x=1$에서만 $f(x) = g(x)$이다.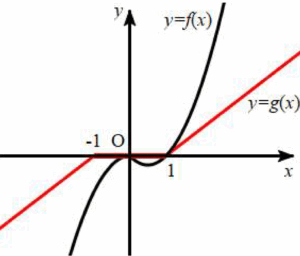 
이때 $x \lt 1$인 모든 실수 $x$에 대하여 $g(x) \ge f(x)$이므로 함수 $h(x)$는 $x = 0$에서 극값을 갖지 않고, $0 \lt x \lt 1$에서 $g(x) \gt f(x)$, $x \gt 1$에서 $f(x) \gt g(x)$이므로 함수 $h(x)$는 $x=1$에서만 극값을 갖는다.
즉, $a \le 1$이면 조건을 만족시킨다.
한편 $a \gt 1$이면 다음 그림과 같이 $x \gt 1$에서 $f(x) = g(x)$인 $x$의 값이 있다. 이 값을 $b$라 하자.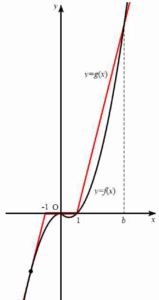 
이때 $f(b) = g(b) = 0$이고 $1 \lt x \lt b$에서 $g(x) \gt f(x)$,
$x \gt b$에서 $f(x) \gt g(x)$이므로 함수 $h(x)$는 $x = b$에서 극값을 갖는다.
그러므로 조건을 만족시키려면 $x \lt -1$에서 $f(x) \gt g(x)$인 구간이 없어야 하므로 $a$의 값은 위 그림과 같이 $x \lt -1$에서 곡선 $y = -x^{2}$과 직선 $y = ax+a$가 접할 때 최대가 된다.
이 접점의 좌표를 $(t, -t^{2})$이라 하면 접선의 기울기가 $-2t$이므로 접선의 방정식은
$y+t^{2} = -2t(x-t)$이다.
이 직선이 점 $(-1, 0)$을 지나야 하므로
$t^{2} = -2t(-1-t)$
$t(t+2) = 0$
$t \lt -1$이므로 $t = -2$
즉, 조건을 만족시키는 $a$의 최댓값은
$-2t = 4$
이므로 $k = 4$
이때, $x \ge 1$에서 $g(x) = 4x-4$이므로
$\displaystyle h(3) = \int_{0}^{3}(g(t)-f(t))dt$
$=\displaystyle \int_{0}^{1}(-t^{2}+t)dt + \int_{1}^{3}\{ (4t-4)-(t^{2}-t) \}dt$
$=\displaystyle \int_{0}^{1}(-t^{2}+t)dt + \int_{1}^{3}(-t^{2}+5t-4)dt$
$=\displaystyle \bigg[ -\frac{1}{3}t^{3}+\frac{1}{2}t^{2} \bigg]_{0}^{1} + \bigg[ -\frac{1}{3}t^{3}+\frac{5}{2}t^{2}-4t \bigg]_{1}^{3}$
$=\displaystyle \frac{1}{6} + \frac{10}{3} = \frac{7}{2}$
따라서 $k + h(3) = 4 + \frac{7}{2} = \dfrac{15}{2}$
16. 수열 $\{ a_n \}$은 $a_{1} = 1$이고, 모든 자연수 $n$에 대하여 $$a_{n+1} = n^{2}a_{n}+1$$ 을 만족시킨다. $a_3$의 값을 구하시오. [3점]
18. $\overline{\mathrm{AB}} = 5$, $\overline{\mathrm{AC}} = 6$이고 $\cos (\angle \mathrm{BAC}) = -\dfrac{3}{5}$인 삼각형 $\mathrm{ABC}$의 넓이를 구하시오. [3점]
$12$
$\cos (\angle \mathrm{BAC}) = -\frac{3}{5}$이고, $\sin (\angle \mathrm{BAC}) \gt 0$이므로
$\sin (\angle \mathrm{BAC}) = \sqrt{1-\cos^{2}(\angle \mathrm{BAC})}$
$= \sqrt{1-(-\frac{3}{5})^{2}} = \sqrt{\frac{16}{25}} = \frac{4}{5}$
따라서 삼각형 $\mathrm{ABC}$의 넓이는
$\frac{1}{2} \times \overline{\mathrm{AB}} \times \overline{\mathrm{AC}} \times \sin (\angle \mathrm{BAC})$
$= \frac{1}{2} \times 5 \times 6 \times \frac{4}{5} = 12$
19. $-2 \le x \le 2$인 모든 실수 $x$에 대하여 부등식 $$-k \le 2x^{3}+3x^{2}-12x-8 \le k$$ 가 성립하도록 하는 양수 $k$의 최솟값을 구하시오. [3점]
$15$
$f(x) = 2x^{3}+3x^{2}-12x-8$이라 하면
$f'(x) = 6x^{2}+6x-12$ $= 6(x+2)(x-1)$
$f'(x) = 0$에서 $x = -2$ 또는 $x = 1$이므로 함수 $f(x)$의 증가와 감소를 표로 나타내면 다음과 같다. 
따라서 함수 $f(x)$는 $x = -2$에서 극댓값 $f(-2) = 12$를 갖고, $x=1$에서 극솟값 $f(1) = -15$를 갖는다.
이때 $f(2) = -4$이므로 $-2 \le x \le 2$에서
$-15 \le f(x) \le 12$
따라서 양수 $k$의 최솟값은 $15$이다.
20. 수열 $\{ a_n \}$이 다음 조건을 만족시킨다.
$\bullet$ $a_{1} = 7$
$\bullet$ $2$ 이상의 자연수 $n$에 대하여
$$\sum_{k=1}^{n}a_{k} = \frac{2}{3}a_{n}+\frac{1}{6}n^{2}-\frac{1}{6}n+10$$
이다.
다음은 $\displaystyle \sum_{k=1}^{12}a_{k}+\sum_{k=1}^{5}a_{2k+1}$의 값을 구하는 과정이다.
$2$ 이상의 자연수 $n$에 대하여 $\displaystyle a_{n+1} = \sum_{k=1}^{n+1}a_{k}-\sum_{k=1}^{n}a_{k}$이므로
$a_{n+1} = \dfrac{2}{3}(a_{n+1}-a_{n}) +\fbox{ $\textbf{(가)}$ }$
이고, 이 식을 정리하면
$2a_{n} + a_{n+1}= 3 \times \fbox{ $\textbf{(가)}$ }$ $\cdots\cdots$ ㉠
이다.
$\displaystyle \sum_{k=1}^{n}a_{k} = \frac{2}{3}a_{n}+\frac{1}{6}n^{2}-\frac{1}{6}n+10$ ($n \ge 2$)
에서 양변에 $n = 2$를 대입하면
$a_{2} = \fbox{ $\textbf{(나)}$ }$ $\cdots\cdots$ ㉡
이다. ㉠과 ㉡에 의하여
$\displaystyle \sum_{k=1}^{12}a_{k}+\sum_{k=1}^{5}a_{2k+1} = a_{1}+a_{2}+\sum_{k=1}^{5}(2a_{2k+1}+a_{2k+2})$
$= \fbox{ $\textbf{(다)}$ }$
이다.
위의 (가)에 알맞은 식을 $f(n)$이라 하고, (나), (다)에 알맞은 수를 각각 $p$, $q$라 할 때, $\dfrac{p \times q}{f(12)}$의 값을 구하시오. [4점]
$130$
$2$ 이상의 자연수 $n$에 대하여
$\displaystyle a_{n+1} = \sum_{k=1}^{n+1}a_{k}-\sum_{k=1}^{n}a_{k}$이므로
$a_{n+1} = \{\frac{2}{3}a_{n+1}+\frac{1}{6}(n+1)^{2}-\frac{1}{6}(n+1)+10 \}-(\frac{2}{3}a_{n}+\frac{1}{6}n^{2}-\frac{1}{6}n+10)$
$= \frac{2}{3}(a_{n+1}-a_{n}) + \fbox{$\frac{1}{3}n$}$이고,
이 식을 정리하면
$2a_{n}+a_{n+1} = 3 \times \fbox{$\frac{1}{3}n$}$
즉, $2a_{n}+a_{n+1} = n$ $\cdots\cdots$ ㉠
이다.
$\displaystyle \sum_{k=1}^{n}a_{k} = \frac{2}{3}a_{n}+\frac{1}{6}n^{2}-\frac{1}{6}n+10$ ($n \ge 2$)
에서 양변에 $n = 2$를 대입하면
$a_{1}+a_{2} = \frac{2}{3}a_{2}+\frac{1}{6}\times 2^{2}-\frac{1}{6}\times 2+10$
즉, $a_{1} + \frac{1}{3}a_{2} = \frac{31}{3}$
$a_{1} = 7$이므로
$a_{2} = 3 \times (\frac{31}{3}-7) = \fbox{$10$}$ $\cdots\cdots$ ㉡
이다. ㉠과 ㉡에 의하여
$\displaystyle \sum_{k=1}^{12}a_{k}+\sum_{k=1}^{5}a_{2k+1}$
$= (a_{1}+a_{2}+a_{3}+ \cdots +a_{12})+(a_{3}+a_{5}+a_{7}+a_{9}+a_{11})$
$= a_{1}+a_{2}+2(a_{3}+a_{5}+a_{7}+a_{9}+a_{11})+(a_{4}+a_{6}+a_{8}+a_{10}+a_{12})$
$\displaystyle= a_{1}+a_{2}+\sum_{k=1}^{5}(2a_{2k+1}+a_{2k+2})$
$\displaystyle= a_{1}+a_{2}+\sum_{k=1}^{5}(2k+1)$
$= 7+10+(3+5+7+9+11)$
$= 17 + 7\times 5 = \fbox{$52$}$
이다.
이때 $f(n) = \frac{1}{3}n$, $p = 10$, $q = 52$이므로
$\dfrac{p \times q}{f(12)} = \dfrac{10 \times 52}{4} = 130$
21. 최고차항의 계수가 양수인 삼차함수 $f(x)$와 실수 $t$에 대하여 함수 $$g(x) = \begin{cases} -f(x) & (x \lt t) \\ \\ f(x) & (x \ge t) \end{cases}$$ 는 실수 전체의 집합에서 연속이고 다음 조건을 만족시킨다.
(가) 모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a+}\frac{g(x)}{x(x-2)}$의 값이 존재한다.
(나) $\displaystyle \lim_{x \to m+}\frac{g(x)}{x(x-2)}$의 값이 음수가 되도록 하는 자연수 $m$의 집합은 $\left\{ g(-1), \:-\dfrac{7}{2}g(1) \right\}$이다.
$g(-5)$의 값을 구하시오. (단, $g(-1) \ne -\dfrac{7}{2}g(1)$) [4점]
$65$
다항함수 $f(x)$는 실수 전체의 집합에서 연속이므로 함수 $g(x)$가 실수 전체의 집합에서 연속이려면
$\displaystyle \lim_{x \to t-}g(x) = \lim_{x \to t+}g(x) = g(t)$
즉, $\displaystyle \lim_{x \to t-}(-f(x)) = \lim_{x \to t+}f(x) = f(t)$ $\cdots\cdots$ ㉠
이어야 한다.
그런데
$\displaystyle \lim_{x \to t-}(-f(x)) = -f(t)$, $\displaystyle \lim_{x \to t+}f(x) = f(t)$
이므로 ㉠에서
$f(t) = -f(t)$, 즉 $f(t) = 0$
조건 (가)에서 $a = 0$ 또는 $a = 2$일 때에도 $\displaystyle \lim_{x \to a+}\frac{g(x)}{x(x-2)}$의 값이 존재해야 하므로
$g(0) = g(2) = 0$, 즉 $f(0) = f(2) = 0$
그러므로
$f(x) = \alpha x(x-2)(x-k)$ ($k$는 상수) $\cdots\cdots$ ㉡
로 놓을 수 있다.
한편, 자연수 $m$에 대하여 조건 (나)에서 $\displaystyle \lim_{x \to m+}\frac{g(x)}{x(x-2)} \lt 0$일 조건은 다음과 같다.
(ⅰ) $m = 1$일 때
$\displaystyle \lim_{x \to 1+}x(x-2) = 1\times (1-2) \lt 0$이므로 $g(1) \gt 0$이어야 한다.
이때 $-\frac{7}{2}g(1) \lt 0$이므로 조건 (나)에서 $-\frac{7}{2}g(1)$이 자연수라는 조건에 모순이다.
그러므로 $1$은 조건 (나)를 만족시키는 자연수 $m$이 될 수 없다.
(ⅱ) $m = 2$일 때
$\displaystyle \lim_{x \to 2+}\frac{g(x)}{x(x-2)}$ $= \displaystyle \lim_{x \to 2+}\frac{1}{x}\times \lim_{x \to 2+}\frac{g(x)-g(2)}{x-2}$
$= \displaystyle \frac{1}{2}\times \lim_{x \to 2+}\frac{g(x)-g(2)}{x-2} \lt 0$
이므로
$= \displaystyle \lim_{x \to 2+}\frac{g(x)-g(2)}{x-2} \lt 0$
이어야 한다.
(ⅲ) $m \gt 2$일 때
$\displaystyle \lim_{x \to m+}\frac{g(x)}{x(x-2)} = \frac{g(m)}{m(m-2)}$이고 $m(m-2) \gt 0$이므로
$g(m) \lt 0$이어야 한다.
(ⅰ), (ⅱ), (ⅲ)에서 $\displaystyle \lim_{x \to m+}\frac{g(x)}{x(x-2)} \lt 0$인 자연수 $m$의 개수가 $2$이려면
$g(m) \lt 0$이고 $m \gt 2$인 자연수 $m$이 적어도 한 개 존재해야 한다.
그러므로 ㉡에서
$f(x) = \alpha x(x-2)(x-k)$ ($k \gt 3$)
이고, 조건 (나)에서
$g(-1) \gt 0$, $g(1) \lt 0$이므로 $t = 2$이어야 한다.
$g(x) = \begin{cases} -\alpha x(x-2)(x-k) & (x \lt 2) \\ \alpha x(x-2)(x-k) & (x \ge 2) \end{cases}$
이다.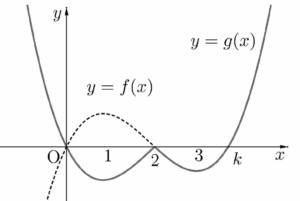 
이때 $2$와 $3$이 조건 (나)를 만족시키므로 $3 \lt k \le 4$이어야 한다.
한편,
$g(-1) = 3\alpha (k+1)$, $g(1) = -\alpha (k-1)$
이고, 조건 (나)에서
$g(-1) = 2$, $-\frac{7}{2}g(1) = 3$
또는
$g(-1) = 3$, $-\frac{7}{2}g(1) = 2$
이다.
① $g(-1) = 2$, $-\frac{7}{2}g(1) = 3$일 때
$3\alpha (k+1) = 2$에서 $\alpha = \frac{2}{3(k+1)}$
$-\frac{7}{2}\{ -\alpha (k-1)\} = 3$에서 $\alpha = \frac{6}{7(k-1)}$
$\frac{2}{3(k+1)} = \frac{6}{7(k-1)}$에서 $7(k-1) = 9(k+1)$
$7k-7 = 9k+9$, $k = -8$
이는 $3 \lt k \le 4$에 모순이다.
② $g(-1) = 3$, $-\frac{7}{2}g(1) = 2$일 때
$3\alpha (k+1) = 3$에서 $\alpha = \frac{1}{k+1}$
$-\frac{7}{2}\{ -\alpha (k-1)\} = 2$에서 $\alpha = \frac{4}{7(k-1)}$
$\frac{1}{k+1} = \frac{4}{7(k-1)}$에서 $7(k-1) = 4(k+1)$
$7k-7 = 4k+4$, $k = \frac{11}{3}$
이는 $3 \lt k \le 4$를 만족시킨다.
$k = \frac{11}{3}$일 때 $\alpha = \frac{1}{k+1} = \frac{3}{14}$
그러므로
$g(-5) = -\frac{3}{14} \times (-5) \times (-7) \times (-\frac{26}{3})$ $= 65$
22. 곡선 $y = \log_{16}(8x+2)$ 위의 점 $\mathrm{A}(a, b)$와 곡선 $y = 4^{x-1}-\dfrac{1}{2}$ 위의 점 $\mathrm{B}$가 제$1$사분면에 있다.
점 $\mathrm{A}$를 직선 $y = x$에 대하여 대칭이동한 점이 직선 $\mathrm{OB}$ 위에
있고 선분 $\mathrm{AB}$의 중점의 좌표가 $\left( \dfrac{77}{8}, \dfrac{133}{8} \right)$일 때, $a \times b = \dfrac{q}{p}$이다. $p+q$의 값을 구하시오.
(단, $\mathrm{O}$는 원점이고, $p$와 $q$는 서로소인 자연수이다.) [4점]
$457$
$y = \log_{16}(8x+2)$에서
$16^{y} = 8x+2$ $\cdots\cdots$ ㉠
$y = 4^{x-1}-\frac{1}{2}$에서
$4^{x} = 4y+2$ $\cdots\cdots$ ㉡
이므로 ㉠에서 $y$ 대신에 $\frac{x}{2}$, $x$ 대신에 $\frac{y}{2}$를 대입하면 ㉡과 일치한다. $\cdots\cdots$ (ⅰ)
점 $\mathrm{A}(a, b)$가 곡선 $y = \log_{16}(8x+2)$ 위의 점이므로
$16^{b} = 8a+2$
또한 $\mathrm{B}(c, d)$라 하면 점 $\mathrm{B}$는 곡선 $y = 4^{x-1}-\frac{1}{2}$ 위의 점이므로
$4^{c} = 4d+2$
그리고 점 $\mathrm{A}$를 직선 $y=x$에 대하여 대칭이동한 점 $(b, a)$가 직선 $\mathrm{OB}$ 위에 있어야 하므로
$a = \frac{d}{c} \times b$, $ac-bd = 0$ $\cdots\cdots$ ㉢
이때 (ⅰ)에 의하여
$a = \frac{d}{2}$, $b = \frac{c}{2}$ 즉 $d = 2a$, $c = 2b$ $\cdots\cdots$ ㉣
이고 이 관계는 ㉢을 만족시킨다.
따라서 선분 $\mathrm{AB}$의 중점의 좌표가 $(\frac{77}{8}, \frac{133}{8})$이므로
$\frac{a+c}{2} = \frac{77}{8}$, $\frac{b+d}{2} = \frac{133}{8}$
$a+c = \frac{77}{4}$, $b+d = \frac{133}{4}$
$a+2b = \frac{77}{4}$, $2a+b = \frac{133}{4}$
따라서 $a = \frac{63}{4}$, $b = \frac{7}{4}$이므로
$a \times b = \frac{441}{16}$
즉 $p = 16$, $q = 441$이므로
$p+q = 457$
수학 영역(확률과 통계)
24. 두 사건 $A$, $B$에 대하여 $$\mathrm{P}(A) = \frac{2}{5}, \:\mathrm{P}(B\,| A) = \frac{1}{4}, \:\mathrm{P}(A \cup B) = 1$$ 일 때, $\mathrm{P}(B)$의 값은? [3점]
① $\frac{7}{10}$
② $\frac{3}{4}$
③ $\frac{4}{5}$
④ $\frac{17}{20}$
⑤ $\frac{9}{10}$
①
$\mathrm{P}(A) = \frac{2}{5}$
$\mathrm{P}(B\,| A) = \frac{\mathrm{P}(A \cap B)}{\mathrm{P}(A)} = \frac{1}{4}$에서
$\mathrm{P}(A \cap B) = \frac{1}{4} \times \mathrm{P}(A)$ $= \frac{1}{4} \times \frac{2}{5} = \frac{1}{10}$
$\mathrm{P}(A \cup B) = 1$에서 $\mathrm{P}(A)+\mathrm{P}(B)-\mathrm{P}(A \cap B) = 1$
즉, $\frac{2}{5}+\mathrm{P}(B)-\frac{1}{10} = 1$이므로
$\mathrm{P}(B) = 1-\frac{2}{5}+\frac{1}{10}$ $= \dfrac{7}{10}$
25. 주머니에 숫자 $1$, $2$, $3$, $4$, $5$가 하나씩 적혀 있는 흰 공 $5$개와 숫자 $2$, $3$, $4$, $5$, $6$이 하나씩 적혀 있는 검은 공 $5$개가 들어 있다. 이 주머니에서 임의로 $2$개의 공을 동시에 꺼낼 때, 꺼낸 $2$개의 공이 서로 같은 색이거나 꺼낸 $2$개의 공에 적힌 수가 서로 같을 확률은? [3점]
① $\frac{7}{15}$
② $\frac{8}{15}$
③ $\frac{3}{5}$
④ $\frac{2}{3}$
⑤ $\frac{11}{15}$
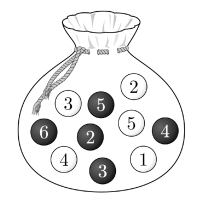
②
$10$개의 공 중 임의로 $2$개의 공을 동시에 꺼내는 경우의 수는
${}_{10}\mathrm{C}_{2} = \frac{10 \times 9}{2} = 45$
이므로 꺼낸 $2$개의 공이 서로 같은 색일 확률은
$\frac{2 \times {}_{5}\mathrm{C}_{2}}{45} = \frac{20}{45} = \frac{4}{9}$
꺼낸 $2$개의 공에 적힌 수가 서로 같을 확률은
$\frac{4}{45}$
꺼낸 $2$개의 공이 서로 같은 색인 사건과 공에 적힌 수가 서로 같은 사건은 서로 배반사건이므로 구하는 확률은
$\frac{4}{9}+\frac{4}{45} = \dfrac{8}{15}$
26. 평균이 $m$이고 표준편차가 $5$인 정규분포를 따르는 모집단에서 크기가 $36$인 표본을 임의추출하여 얻은 표본평균을 이용하여 구한 모평균 $m$에 대한 신뢰도 $99$%의 신뢰구간이 $1.2 \le m \le a$이다. $a$의 값은?
(단, $Z$가 표준정규분포를 따르는 확률변수일 때, $\mathrm{P}(|Z| \le 2.58) = 0.99$로 계산한다. [3점]
① $5.1$
② $5.2$
③ $5.3$
④ $5.4$
⑤ $5.5$
⑤
모집단의 표준편차가 $5$이므로 모집단에서 크기가 $36$인 표본을 임의추출하여 얻은 표본평균을 $\bar{x}$라 하면 모평균 $m$에 대한 신뢰도 $99$%의 신뢰구간은
$\bar{x}-2.58\times \frac{5}{\sqrt{36}} \le m \le \bar{x}+2.58\times \frac{5}{\sqrt{36}}$
이다.
즉, $\bar{x}-2.15 \le m \le \bar{x}+2.15$
한편, 모평균 $m$에 대한 신뢰도 $99$%의 신뢰구간이 $1.2 \le m \le a$이므로
$\bar{x}-2.15 = 1.2$ $\cdots\cdots$ ㉠
$\bar{x}+2.15 = a$ $\cdots\cdots$ ㉡
㉡$\,-\,$㉠을 하면
$2.15-(-2.15) = a-1.2$
$4.3 = a-1.2$
따라서 $a = 4.3+1.2 = 5.5$
27. 이산확률변수 $X$가 가지는 값이 $0$부터 $4$까지의 정수이고 $$\mathrm{P}(X = x) = \begin{cases} \dfrac{|2x-1|}{12} & (x = 0, 1, 2, 3) \\ \\ \:a & (x = 4) \end{cases}$$ 일 때, $\mathrm{V}\left(\dfrac{1}{a}X\right)$의 값은? (단, $a$는 $0$이 아닌 상수이다.) [3점]
① $36$
② $39$
③ $42$
④ $45$
⑤ $48$
④
확률변수 $X$가 가지는 모든 값에 대한 확률의 합은 $1$이므로
$\frac{1}{12}+\frac{1}{12}+\frac{3}{12}+\frac{5}{12}+a = 1$에서
$a = \frac{1}{6}$
$\mathrm{E}(X)$ $= 0\times \frac{1}{12}+1\times \frac{1}{12}+2\times \frac{3}{12}+3\times \frac{5}{12}+4\times \frac{1}{6} = \frac{30}{12} = \frac{5}{2}$,
$\mathrm{E}(X^{2})$ $= 0^{2}\times \frac{1}{12}+1^{2}\times \frac{1}{12}+2^{2}\times \frac{3}{12}+3^{2}\times \frac{5}{12}+4^{2}\times \frac{1}{6} = \frac{90}{12} = \frac{15}{2}$
이므로
$\mathrm{V}(X) = \mathrm{E}(X^{2})-(\mathrm{E}(X))^{2}$ $= \frac{15}{2}-\frac{25}{4} = \frac{5}{4}$
따라서 $\mathrm{V}(\frac{1}{a}X) = \mathrm{V}(6X) = 36\mathrm{V}(X)$ $= 36 \times \frac{5}{4} = 45$
28. $16$개의 공과 $1$부터 $6$까지의 자연수가 하나씩 적혀 있는 여섯 개의 빈 상자가 있다. 한 개의 주사위를 사용하여 다음 시행을 한다.
주사위를 한 번 던져 나온 눈의 수가 $k$일 때,
$k$가 홀수이면
$1$, $3$, $5$가 적힌 상자에 공을 각각 $1$개씩 넣고,
$k$가 짝수이면
$k$의 약수가 적힌 상자에 공을 각각 $1$개씩 넣는다.
이 시행을 $4$번 반복한 후 여섯 개의 상자에 들어 있는 모든 공의 개수의 합이 홀수일 때, $3$이 적힌 상자에 들어 있는 공의 개수가 $2$가 적힌 상자에 들어 있는 공의 개수보다 $1$개 더 많을 확률은? [4점]
① $\frac{1}{8}$
② $\frac{3}{16}$
③ $\frac{1}{4}$
④ $\frac{5}{16}$
⑤ $\frac{3}{8}$
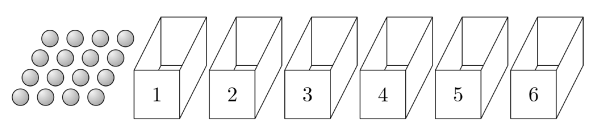
②
주어진 시행은 한 개의 주사위를 한 번 던져 나온 눈의 수가 홀수이면 $1$, $3$, $5$가 적힌 상자에 공을 각각 $1$개씩 넣고, 나온 눈의 수가 $2$이면 $1$, $2$가 적힌 상자에 공을 각각 $1$개씩 넣고, 나온 눈의 수가 $4$이면 $1$, $2$, $4$가 적힌 상자에 공을 각각 $1$개씩 넣고, 나온 눈의 수가 $6$이면 $1$, $2$, $3$, $6$이 적힌 상자에 공을 각각 $1$개씩 넣는 시행이다.
이 시행을 $4$번 반복한 후 여섯 개의 상자에 들어 있는 모든 공의 개수의 합이 홀수인 사건을 $A$, $3$이 적힌 상자에 들어 있는 공의 개수가 $2$가 적힌 상자에 들어 있는 공의 개수보다 $1$개 더 많은 사건을 $B$라 하면 구하는 확률은 $\mathrm{P}(B\, | A)$이다.
사건 $A$는 다음의 네 가지 경우이다.
(ⅰ) $4$번의 시행에서 나온 눈의 수가 홀수인 경우가 $3$번일 때
나온 눈의 수가 $2$ 또는 $6$인 경우가 $1$번이어야 하므로 이 경우의 확률은
$\frac{4!}{3!}\times (\frac{3}{6})^{3}(\frac{2}{6})^{1} = \frac{216}{6^{4}}$
(ⅱ) $4$번의 시행에서 나온 눈의 수가 홀수인 경우가 $2$번일 때
나온 눈의 수가 $4$인 경우가 $1$번, $2$ 또는 $6$인 경우가 $1$번이어야 하므로 이 경우의 확률은
$\frac{4!}{2!}\times (\frac{3}{6})^{2}(\frac{1}{6})^{1}(\frac{2}{6})^{1} = \frac{216}{6^{4}}$
(ⅲ) $4$번의 시행에서 나온 눈의 수가 홀수인 경우가 $1$번일 때
나온 눈의 수가 $4$인 경우가 $2$번, $2$ 또는 $6$인 경우가 $1$번이거나 나온 눈의 수가 $2$ 또는 $6$인 경우가 $3$번이어야 하므로 이 경우의 확률은
$\frac{4!}{2!}\times (\frac{3}{6})^{1}\times (\frac{1}{6})^{2}(\frac{2}{6})^{1}+\frac{4!}{3!}\times (\frac{3}{6})^{1}(\frac{2}{6})^{3} = \frac{168}{6^{4}}$
(ⅳ) $4$번의 시행에서 나온 눈의 수가 모두 짝수일 때
나온 눈의 수가 $4$인 경우가 $1$번, $2$ 또는 $6$인 경우가 $3$번이거나 나온 눈의 수가 $4$인 경우가 $3$번, $2$ 또는 $6$인 경우가 $1$번이어야 하므로 이 경우의 확률은
$\frac{4!}{3!}\times (\frac{1}{6})^{1}(\frac{2}{6})^{3}+\frac{4!}{3!}\times (\frac{1}{6})^{3}(\frac{2}{6})^{1} = \frac{40}{6^{4}}$
(ⅰ) ~ (ⅳ)에서
$\mathrm{P}(A) = \frac{216}{6^{4}}+\frac{216}{6^{4}}+\frac{168}{6^{4}}+\frac{40}{6^{4}} = \frac{640}{6^{4}}$
한편, 사건 $A \cap B$는 $4$번의 시행에서 나온 눈의 수가 홀수인 경우가 $2$번, $4$인
경우가 $1$번, $6$인 경우가 $1$번이거나 나온 눈의 수가 홀수인 경우가 $1$번, $6$인 경우가 $3$번이어야 하므로 이 경우의 확률은
$\frac{4!}{2!}\times (\frac{3}{6})^{2}(\frac{1}{6})^{1}(\frac{1}{6})^{1}+\frac{4!}{3!}\times (\frac{3}{6})^{1}(\frac{1}{6})^{3} = \frac{120}{6^{4}}$
따라서 구하는 확률은
$\mathrm{P}(B\,|A) = \dfrac{\mathrm{P}(B\cap A)}{\mathrm{P}(A)} = \dfrac{\frac{120}{6^{4}}}{\frac{640}{6^{4}}} = \dfrac{3}{16}$
29. $6$ 이하의 자연수 $a$에 대하여 한 개의 주사위와 한 개의 동전을 사용하여 다음 시행을 한다.
주사위를 한 번 던져
나온 눈의 수가 $a$ 보다 작거나 같으면
동전을 $5$번 던져 앞면이 나온 횟수를 기록하고,
나온 눈의 수가 $a$ 보다 크면
동전을 $3$번 던져 앞면이 나온 횟수를 기록한다.
이 시행을 
$19200$번 반복하여 기록한 수가 $3$인 횟수를 확률변수 $X$라 하자.
$\mathrm{E}(X) = 4800$일 때, $\mathrm{P}(X \le 4800+30a)$의 값을 오른쪽 표준정규분포표를 이용하여 구한 값이 $k$이다.
$1000 \times k$의 값을 구하시오. [4점]
$977$
한 개의 주사위를 한 번 던져 나온 눈의 수가 $a$ 보다 작거나 같을 확률은 $\frac{a}{6}$이고, $a$ 보다 클 확률은 $\frac{6-a}{6}$이므로 주어진 시행을 한 번 하여 기록한 수가 $3$일 확률은
$\frac{a}{6}\times {}_{5}\mathrm{C}_{3} \times (\frac{1}{2})^{3}\times (\frac{1}{2})^{2}+\frac{6-a}{6}\times {}_{3}\mathrm{C}_{3} \times (\frac{1}{2})^{3}\times (\frac{1}{2})^{0}$
$= \frac{a+4}{32}$
따라서 확률변수 $X$는 이항분포 $\mathrm{B}(19200, \frac{a+4}{32})$를 따른다.
$\mathrm{E}(X) = 19200\times \frac{a+4}{32} = 4800$에서
$a = 4$
즉, 확률변수 $X$는 이항분포 $\mathrm{B}(19200, \frac{1}{4})$을 따른다.
이때, $\mathrm{V}(X) = 19200\times \frac{1}{4} \times \frac{3}{4} = 3600$이고,
$19200$은 충분히 큰 수이므로 확률변수 $X$는 근사적으로 정규분포 $\mathrm{N}(4800, 60^{2})$을 따른다.
따라서
$k = \mathrm{P}(X \le 4800+30a)$
$= \mathrm{P}(X \le 4920)$
$= \mathrm{P}(Z \le \frac{4920-4800}{60})$
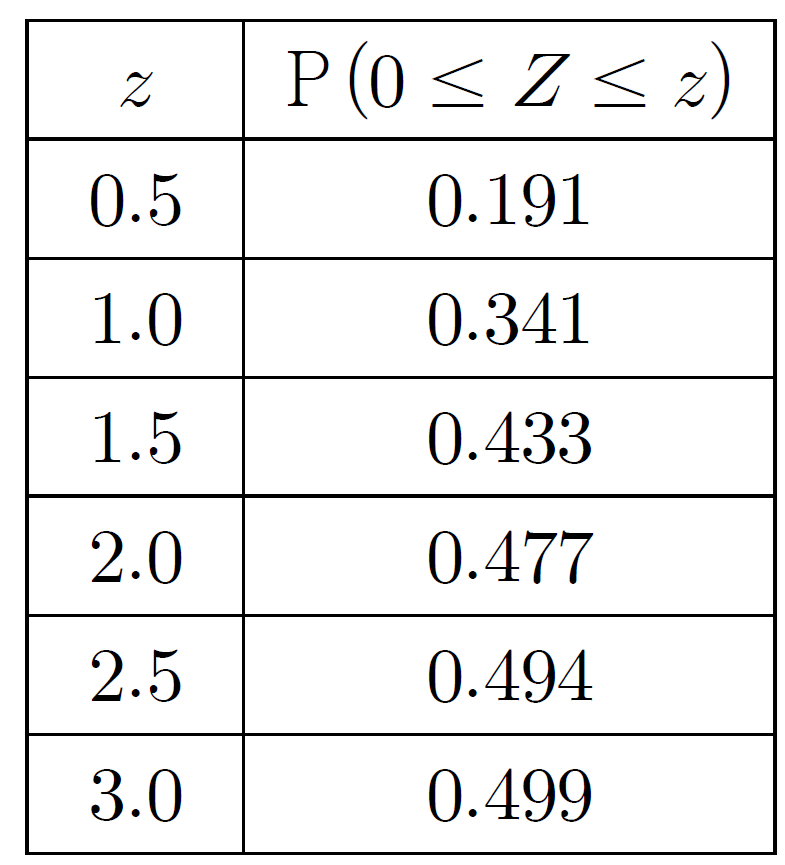
$= \mathrm{P}(Z \le 2)$
$= 0.5+\mathrm{P}(0 \le Z \le 2)$
$= 0.5+0.477$
$= 0.977$
따라서 $1000 \times k = 1000 \times 0.977 = 977$
30. 비어 있는 주머니 $10$개가 일렬로 놓여 있고, 공 $8$개가 있다. 각 주머니에 들어 있는 공의 개수가 $2$ 이하가 되도록 공을 주머니에 남김없이 나누어 넣을 때, 다음 조건을 만족시키는 경우의 수를 구하시오. (단, 공끼리는 서로 구별하지 않는다.) [4점]
(가) 들어 있는 공의 개수가 $1$인 주머니는 $4$개 또는 $6$개이다.
(나) 들어 있는 공의 개수가 $2$인 주머니와 이웃한 주머니에는 공이 들어 있지 않다.
$262$
조건 (가)에 의해 들어 있는 공의 개수가 $1$인 주머니는 $4$개 또는 $6$개이다.
(ⅰ) 들어 있는 공의 개수가 $1$인 주머니가 $4$개일 때
공이 모두 $8$개이고, 각 주머니에 들어 있는 공의 개수가 $2$ 이하이므로 들어 있는 공의 개수가 $2$인 주머니는 $2$이고, 들어 있는 공의 개수가 $0$인 주머니는 $4$개이다.
조건 (나)에서 들어 있는 공의 개수가 $2$인 주머니와 이웃한 주머니에는 공이 들어 있지 않아야 하므로 먼저 들어 있는 공의 개수가 $0$인 주머니 $4$개를 각각 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$, $\mathrm{A}_4$라 하고, 네 주머니 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$, $\mathrm{A}_4$가 다음과 같이 놓여 있다고 하자.
$\vee\mathrm{A}_{1} \vee\mathrm{A}_{2}\vee\mathrm{A}_{3}\vee\mathrm{A}_{4}\vee$
네 주머니 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$, $\mathrm{A}_4$의 사이 사이와 맨 앞, 맨 뒤 중 들어 있는 공의 개수가 $2$인 주머니 $2$개를 놓을 위치를 택하는 경우의 수는
${}_{5}\mathrm{C}_{2} = \frac{5\times 4}{2\times 1} = 10$
들어 있는 공의 개수가 $2$인 주머니 $2$개를 $\mathrm{B}_1$, $\mathrm{B}_2$라 하고, 주머니 가 다음과 같이 놓여 있다고 하자.
$\mathrm{B}_{1}\,\mathrm{A}_{1} \vee\mathrm{A}_{2}\vee\mathrm{A}_{3}\,\mathrm{B}_{2}\,\mathrm{A}_{4}\vee$ $\cdots\cdots$ ㉠
들어 있는 공의 개수가 $1$인 주머니 $4$개를 나열하는 경우의 수는 ㉠의 $\vee$ 표시된 $3$곳 중에서 $4$개를 택하는 중복조합의 수와 같으므로
${}_{3}\mathrm{H}_{4} = {}_{3+4-1}\mathrm{C}_{4} = {}_{6}\mathrm{C}_{4} = {}_{6}\mathrm{C}_{2} = \frac{6\times 5}{2\times 1} = 15$
그러므로 이때의 경우의 수는
$10 \times 15 = 150$
(ⅱ) 들어 있는 공의 개수가 $1$인 주머니가 $6$개일 때
공이 모두 $8$개이고, 각 주머니에 들어 있는 공의 개수가 $2$ 이하이므로 들어 있는 공의 개수가 $2$인 주머니는 $1$개이고, 들어 있는 공의 개수가 $0$인 주머니는 $3$개이다.
조건 (나)에서 들어 있는 공의 개수가 $2$인 주머니와 이웃한 주머니에는 공이 들어 있지 않아야 하므로 먼저 들어 있는 공의 개수가 $0$인 주머니 $3$개를 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$이라 하고, 세 주머니 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$이 다음과 같이 놓여 있다고 하자.
$\vee\mathrm{A}_{1} \vee\mathrm{A}_{2}\vee\mathrm{A}_{3}\vee$
세 주머니 $\mathrm{A}_1$, $\mathrm{A}_2$, $\mathrm{A}_3$의 사이 사이와 맨 앞, 맨 뒤 중 들어 있는 공의 개수가 $2$인 주머니 $1$개를 놓을 위치를 택하는 경우의 수는
${}_{4}\mathrm{C}_{1} = 4$
들어 있는 공의 개수가 $2$인 주머니 $1$개를 $\mathrm{B}_1$이라 하고, 주머니 $\mathrm{B}_1$이 다음과 같이 놓여 있다고 하자.
$\mathrm{B}_{1}\,\mathrm{A}_{1} \vee\mathrm{A}_{2}\vee\mathrm{A}_{3}\vee$ $\cdots\cdots$ ㉡
들어 있는 공의 개수가 $1$인 주머니 $6$개를 나열하는 경우의 수는 ㉡의 $\vee$ 표시된 $3$곳 중에서 $6$개를 택하는 중복조합의 수와 같으므로
${}_{3}\mathrm{H}_{6} = {}_{3+6-1}\mathrm{C}_{6} = {}_{8}\mathrm{C}_{6} = {}_{8}\mathrm{C}_{2} = \frac{8\times 7}{2\times 1} = 28$
그러므로 이때의 경우의 수는
$4\times 28 = 112$
(ⅰ), (ⅱ)에서 구하는 경우의 수는
$150+112 = 262$
수학 영역(미적분)
23. $\displaystyle \lim_{x \to 0}\frac{\tan 6x}{2x}$의 값은? [2점]
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
24. $\displaystyle \int_{0}^{\frac{\pi}{2}}\sqrt{\sin x-\sin^{3}x} \,dx$의 값은? [3점]
① $\frac{1}{6}$
② $\frac{1}{3}$
③ $\frac{1}{2}$
④ $\frac{2}{3}$
⑤ $\frac{5}{6}$
④
$\sin x-\sin^{3}x = \sin x(1-\sin^{2}x) = \sin x \cos^{2}x$
또한 $\sin x = t$라 하면
$\sin 0 = 0$, $\sin \frac{\pi}{2} = 1$이고
$\cos x = \frac{dt}{dx}$이므로
$\int_{0}^{\frac{\pi}{2}}\sqrt{\sin x-\sin^{3}x} \,dx$
$= \int_{0}^{\frac{\pi}{2}}\sqrt{\sin x \cos^{2}x} \,dx$
$= \int_{0}^{\frac{\pi}{2}}(\sqrt{\sin x}\times \cos x ) dx$
$= \int_{0}^{1} \sqrt{t} dt$
$= \bigg[ \frac{2}{3}t^{\frac{3}{2}}\bigg]_{0}^{1}$
$= \dfrac{2}{3}$
25. 수열 $\{ a_n \}$이 모든 자연수 $n$에 대하여 $$\sqrt{9n^{2}-5}+2n \lt a_{n} \lt 5n+1$$ 을 만족시킬 때, $\displaystyle \lim_{n \to \infty}\frac{(a_{n}+2)^{2}}{na_{n}+5n^{2}-2}$의 값은? [3점]
① $\frac{1}{2}$
② $\frac{3}{2}$
③ $\frac{5}{2}$
④ $\frac{7}{2}$
⑤ $\frac{9}{2}$
③
수열 $\{ a_n \}$이 모든 자연수 $n$에 대하여
$\sqrt{9n^{2}-5}+2n \lt a_{n} \lt 5n+1$을 만족시키므로
$\displaystyle \frac{\sqrt{9n^{2}-5}+2n}{n} \lt \frac{a_{n}}{n} \lt \frac{5n+1}{n}$
이때
$\displaystyle \lim_{n \to \infty}\frac{\sqrt{9n^{2}-5}+2n}{n}$ $= \displaystyle \lim_{n \to \infty} \left( \sqrt{9-\frac{5}{n^{2}}}+2 \right)$ $= 3+2 = 5$
$\displaystyle \lim_{n \to \infty}\frac{5n+1}{n} = \displaystyle \lim_{n \to \infty} \left( 5+\frac{1}{n} \right) = 5$
이므로 수열의 극한의 대소관계에 의하여
$\displaystyle \lim_{n \to \infty}\frac{a_{n}}{n} = 5$
따라서
$\displaystyle \lim_{n \to \infty}\frac{(a_{n}+2)^{2}}{na_{n}+5n^{2}-2}$
$= \displaystyle \lim_{n \to \infty}\frac{(\frac{a_{n}}{n}+\frac{2}{n})^{2}}{\frac{a_{n}}{n}+5-\frac{2}{n^{2}}}$
$= \displaystyle \frac{(5+0)^{2}}{5+5-0} = \dfrac{5}{2}$
26. 그림과 같이 곡선 $y = \sqrt{x+x\ln x}$와 $x$축 및 두 직선 $x=1$, $x=2$로 둘러싸인 부분을 밑면으로 하는 입체도형이 있다. 이 입체도형을 $x$축에 수직인 평면으로 자른 단면이 모두 정삼각형일 때, 이 입체도형의 부피는? [3점]
① $\frac{\sqrt{3}(3+8\ln 2)}{16}$
② $\frac{\sqrt{3}(5+12\ln 2)}{24}$
③ $\frac{\sqrt{3}(1+12\ln 2)}{16}$
④ $\frac{\sqrt{3}(1+2\ln 2)}{4}$
⑤ $\frac{\sqrt{3}(1+9\ln 2)}{12}$
①
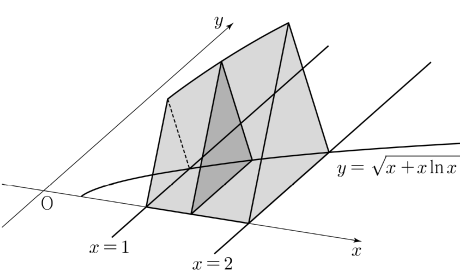
구하는 입체도형의 부피는
$\int_{1}^{2}\frac{\sqrt{3}}{4}(\sqrt{x+x\ln x})^{2}dx$
$= \frac{\sqrt{3}}{4} \int_{1}^{2}(x+x\ln x)dx$
$= \frac{\sqrt{3}}{4} \int_{1}^{2}x(1+\ln x)dx$ $\cdots\cdots$ ㉠
이때 부분적분법에 의하여
$\int_{1}^{2}x(1+\ln x)dx$
$= \bigg[ \frac{x^{2}}{2}(1+\ln x)\bigg]_{1}^{2}-\int_{1}^{2}\left(\frac{x^{2}}{2} \times \frac{1}{x}\right) dx$
$= \{ \frac{4}{2}(1+\ln 2) \}-\{ \frac{1}{2}(1+\ln 1) \}-\int_{1}^{2}\frac{x}{2}dx$
$= \frac{3+4\ln 2}{2}-\bigg[ \frac{x^{2}}{4}\bigg]_{1}^{2}$
$= \frac{3+4\ln 2}{2}-\frac{4-1}{4}$
$= \frac{3+8\ln 2}{4}$
㉠에서 구하는 입체도형의 부피는
$\frac{\sqrt{3}}{4}\times \frac{3+8\ln 2}{4} = \dfrac{\sqrt{3}(3+8\ln 2)}{16}$
27. 매개변수 $t$로 나타내어진 곡선 $$x = e^{4t}(1+\sin^{2}\pi t), \:y = e^{4t}(1-3\cos^{2}\pi t)$$ 를 $C$라 하자. 곡선 $C$가 직선 $y = 3x-5e$와 만나는 점을 $\mathrm{P}$라 할 때, 곡선 $C$ 위의 점 $\mathrm{P}$에서의 접선의 기울기는? [3점]
① $\frac{3\pi-4}{\pi + 4}$
② $\frac{3\pi-2}{\pi + 6}$
③ $\frac{3\pi}{\pi + 8}$
④ $\frac{3\pi+2}{\pi + 10}$
⑤ $\frac{3\pi+4}{\pi + 12}$
②
$x = e^{4t}(1+\sin^{2}\pi t)$, $y = e^{4t}(1-3\cos^{2}\pi t)$를 $y = 3x-5e$에 대입하면
$e^{4t}(1-3\cos^{2}\pi t) = 3e^{4t}(1+\sin^{2}\pi t)-5e$
$e^{4t}\{ -2-3(\cos^{2}\pi t + \sin^{2}\pi t) \} = -5e$
$e^{4t}( -2-3\times 1 ) = -5e$
$e^{4t} = e$
$4t = 1$에서 $t = \frac{1}{4}$
이때
$\frac{dx}{dt} = e^{4t}(4+4\sin^{2}\pi t+2\pi \sin \pi t \cos \pi t)$
$\frac{dy}{dt} = e^{4t}(4-12\cos^{2}\pi t+6\pi \cos \pi t \sin \pi t)$
이므로
$\dfrac{dy}{dx} = \dfrac{\frac{dy}{dt}}{\frac{dx}{dt}}$
$= \dfrac{e^{4t}(4-12\cos^{2}\pi t+6\pi \cos \pi t \sin \pi t)}{e^{4t}(4+4\sin^{2}\pi t+2\pi \sin \pi t \cos \pi t)}$
$= \dfrac{4-12\cos^{2}\pi t+6\pi \cos \pi t \sin \pi t}{4+4\sin^{2}\pi t+2\pi \sin \pi t \cos \pi t}$
위 식에 $t = \frac{1}{4}$을 대입하면
$\dfrac{4-12\times \frac{1}{2}+6\pi \times \frac{\sqrt{2}}{2}\times \frac{\sqrt{2}}{2}}{4+4\times \frac{1}{2}+2\pi \times \frac{\sqrt{2}}{2}\times \frac{\sqrt{2}}{2}}$
$= \dfrac{4-6+3\pi}{4+2+\pi}$ $= \dfrac{3\pi-2}{\pi + 6}$
따라서 곡선 $C$가 직선 $y = 3x-5e$와 만나는 점 $\mathrm{P}$에서의 접선의 기울기는
$\dfrac{3\pi-2}{\pi + 6}$
28. 함수 $$f(x) = \frac{1}{2}x^{2}-x+\ln (1+x)$$ 와 양수 $t$에 대하여 점 $(s, f(s))$ ($s \gt 0$)에서 $y$축에 내린 수선의 발과 곡선 $y = f(x)$ 위의 점 $(s, f(s))$에서의 접선이 $y$축과 만나는 점 사이의 거리가 $t$가 되도록 하는 $s$의 값을 $g(t)$라 하자. $\displaystyle \int_{\frac{1}{2}}^{\frac{27}{4}}g(t) dt$의 값은? [4점]
① $\frac{161}{12}+\ln 3$
② $\frac{40}{3}+\ln 3$
③ $\frac{53}{4}+\ln 2$
④ $\frac{79}{6}+\ln 2$
⑤ $\frac{157}{12}+\ln 2$
⑤
$f(x) = \frac{1}{2}x^{2}-x+\ln (1+x)$에서
$f'(x) = x-1+\frac{1}{x+1} = \frac{x^{2}}{x+1}$
점 $(s, f(s))$ ($s \gt 0$)에서 $y$축에 내린 수선의 발을 $\mathrm{H}$라 하면
$\mathrm{H}(0, f(s))$
또한 곡선 $y = f(x)$ 위의 점 $(s, f(s))$에서의 접선의 방정식은
$y-f(s) = \frac{s^{2}}{s+1}(x-s)$
이고 이 접선이 $y$축과 만나는 점을 $\mathrm{I}$라 하면
$\mathrm{I}(0, -\frac{s^{3}}{s+1}+f(s))$
이때 $s \gt 0$에서 $f'(s) = \frac{s^2}{s+1} \gt 0$이므로
두 점 $\mathrm{H}$, $\mathrm{I}$ 사이의 거리는
$f(s)-(-\frac{s^{3}}{s+1}+f(s)) = \frac{s^{3}}{s+1}$
즉 $t = \dfrac{s^{3}}{s+1}$이다.
이때
$\displaystyle \int_{\frac{1}{2}}^{\frac{27}{4}}g(t) dt = \bigg[ tg(t) \bigg]_{\frac{1}{2}}^{\frac{27}{4}}-\int_{\frac{1}{2}}^{\frac{27}{4}}tg'(t) dt$
이고
$t = \frac{1}{2}$일 때 $\frac{s^{3}}{s+1} = \frac{1}{2}$, $2s^{3}-s-1 = 0$
$(s-1)(2s^{2}+2s+1) = 0$
에서 $s \gt 0$이므로 $s = 1$
$t = \frac{27}{4}$일 때 $\frac{s^{3}}{s+1} = \frac{27}{4}$, $4s^{3}-27s-27 = 0$
$(s-3)(2s+3)^{2} = 0$
에서 $s \gt 0$이므로 $s = 3$
즉 $\bigg[ tg(t) \bigg]_{\frac{1}{2}}^{\frac{27}{4}} = \frac{27}{4}g(\frac{27}{4})-\frac{1}{2}g(\frac{1}{2})$
$= \frac{27}{4}\times 3-\frac{1}{2}\times 1$
$= \frac{79}{4}$
또한 $s = g(t)$이므로 $g'(t) = \frac{ds}{dt}$
따라서
$\int_{\frac{1}{2}}^{\frac{27}{4}}tg'(t) dt = \int_{1}^{3}\frac{s^{3}}{s+1} ds$
$= \int_{1}^{3}\left( s^{2}-s+1-\frac{1}{s+1} \right) ds$
$= \bigg[ \frac{1}{3}s^{3}-\frac{1}{2}s^{2}+s-\ln |s+1| \bigg]_{1}^{3}$
$= (9-\frac{9}{2}+3-\ln 4)-(\frac{1}{3}-\frac{1}{2}+1-\ln 2)$
$= (\frac{15}{2}-2\ln 2)-(\frac{5}{6}-\ln 2)$
$= \frac{20}{3}-\ln 2$
이므로
$\int_{\frac{1}{2}}^{\frac{27}{4}}g(t) dt$ $= \frac{79}{4}-(\frac{20}{3}-\ln 2)$ $= \dfrac{157}{12}-\ln 2$
29. 첫째항과 공차가 같은 등차수열 $\{ a_n \}$과 등비수열 $\{ b_n \}$이 다음 조건을 만족시킨다.
어떤 자연수 $k$에 대하여 $$b_{k+1}= \frac{1}{a_i}-1\:\:(i = 1, 2, 3)$$ 이다.
부등식 $$0 \lt \sum_{n = 1}^{\infty}\left( b_{n}-\frac{1}{a_{n}a_{n+1}} \right) \lt 30$$ 이 성립할 때, $\displaystyle a_{2}\times \sum_{n = 1}^{\infty}b_{2n} = \frac{q}{p}$이다. $p+q$의 값을 구하시오. (단, $a_{1} \ne 0$이고, $p$와 $q$는 서로소인 자연수이다.) [4점]
$97$
등차수열 $\{ a_n \}$의 공차를 $d$라 하면 첫째 항도 $d$이므로
$a_{n}= d+(n-1)d = nd$ ($n = 1, 2, 3, \cdots$)
이때 어떤 자연수 $k$에 대하여
$b_{k+1} = \frac{1}{a_1}-1 = \frac{1}{d}-1$
$b_{k+2} = \frac{1}{a_2}-1 = \frac{1}{2d}-1$
$b_{k+3} = \frac{1}{a_3}-1 = \frac{1}{3d}-1$
이고 수열 $\{ b_n \}$은 등비수열이므로
$(\frac{1}{2d}-1)^{2} = (\frac{1}{d}-1)(\frac{1}{3d}-1)$
$\frac{1}{4d^{2}}-\frac{1}{d}+1 = \frac{1}{3d^{2}}-\frac{1}{d}-\frac{1}{3d}+1$
$\frac{1}{12d^{2}} = \frac{1}{3d}$
$d = \frac{1}{4}$
이때 $b_{k+1} = 3$, $b_{k+2} = 1$, $b_{k+3} = \frac{1}{3}$이므로 등비수열 $\{ b_n \}$의 공비는 $\frac{1}{3}$이고 첫째항 $b_1$은 $3$의 거듭제곱 꼴이다.
한편 $\displaystyle 0 \lt \sum_{n = 1}^{\infty}\left( b_{n}-\frac{1}{a_{n}a_{n+1}} \right) \lt 30$에서
$\displaystyle \sum_{n = 1}^{\infty} b_{n} = \frac{b_1}{1-\frac{1}{3}} = \frac{3}{2}b_1$
$\displaystyle \sum_{n = 1}^{\infty}\frac{1}{a_{n}a_{n+1}} = \sum_{n = 1}^{\infty}\frac{16}{n(n+1)}$
$= \displaystyle \lim_{n \to \infty}16\sum_{k=1}^{n}\left(\frac{1}{k}-\frac{1}{k+1}\right)$
$= \displaystyle \lim_{n \to \infty}16\left(1-\frac{1}{n+1}\right) = 16$
이므로
$0 \lt \frac{3}{2}b_{1}-16 \lt 30$
$\frac{32}{3} \lt b_1 \lt \frac{92}{3}$
이때 $b_1$은 $3$의 거듭제곱 꼴이어야 하므로 $b_{1} = 27$
즉, $a_{n} = \frac{n}{4}$이고, 수열 $\{ b_{2n} \}$은 첫째항이 $b_{2} = b_{1}\times \frac{1}{3} = 27\times \frac{1}{3} = 9$, 공비가 $(\frac{1}{3})^{2} = \frac{1}{9}$인 등비수열이므로
$\displaystyle a_{2}\times \sum_{n = 1}^{\infty}b_{2n}$
$= \dfrac{2}{4}\times \dfrac{9}{1-\frac{1}{9}}$
$= \dfrac{1}{2}\times \dfrac{81}{8} = \dfrac{81}{16}$
따라서 $p = 16$, $q = 81$이므로
$p+q = 97$
30. 실수 전체의 집합에서 증가하는 연속함수 $f(x)$의 역함수 $f^{-1}(x)$가 다음 조건을 만족시킨다.
(가) $|x| \le 1$일 때, $4\times (f^{-1}(x))^{2} = x^{2}(x^{2}-5)^{2}$이다.
(나) $|x| \gt 1$일 때, $|f^{-1}(x)| = e^{|x|-1}+1$이다.
실수 $m$에 대하여 기울기가 $m$이고 점 $(1, 0)$을 지나는 직선이 곡선 $y = f(x)$와 만나는 점의 개수를 $g(m)$이라 하자. 함수 $g(m)$이 $m = a$, $m = b$ ($a \lt b$)에서 불연속일 때, $\displaystyle g(a) \times \left( \lim_{m \to a+}g(m) \right) + g(b) \times \left( \frac{\ln b}{b} \right)^{2}$의 값을 구하시오. (단, $\displaystyle \lim_{x \to \infty}\frac{\ln x}{x} = 0$) [4점]
$11$
함수 $f(x)$가 실수 전체에서 증가하는 연속함수이므로 역함수 $f^{-1}(x)$도 실수 전체에서 증가하는 연속함수이다.
따라서 조건 (가)에서 $|x| \le 1$일 때
$f^{-1}(x) = -\frac{x}{2}(x^{2}-5)$
이고, 조건 (나)에서 $x \gt 1$일 때 $f^{-1}(x) = e^{x-1}+1$
이며 $x \lt -1$일 때 $f^{-1}(x) = -(e^{-x-1}+1)$이다.
역함수 $y = f^{-1}(x)$의 그래프는 다음과 같다.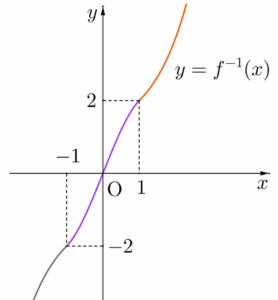
(ⅰ) 점 $(0, 1)$을 지나고 곡선 $y = -\frac{x}{2}(x^{2}-5)$, 즉 $y = -\frac{1}{2}x^{3}+\frac{5}{2}x$에 접하는 직선 $l$의 기울기를 구해보자.
$y’ = -\frac{3}{2}x^{2}+\frac{5}{2}$이므로 접점의 $x$좌표를 $\alpha$라 하면
$\frac{-\frac{1}{2}\alpha^{3}+\frac{5}{2}\alpha-1}{\alpha-0} = -\frac{3}{2}\alpha^{2}+\frac{5}{2}$
$-\alpha^{3}+5\alpha-2 = -3\alpha^{3}+5\alpha$
$\alpha = 1$
따라서 접선 $l$의 기울기는 $1$이다.
한편, $y = e^{x-1}+1$에서 $y’ = e^{x-1}$이므로 이 곡선 위의 점 $(1, 2)$에서의 접선의 기울기도 $1$이다.
(ⅱ) 점 $(0, 1)$을 지나고 곡선 $y = -(e^{-x-1}+1)$, 즉 $y = -e^{-x-1}-1$에 접하는 직선 $m$의 기울기를 구해 보자.
$y’ = e^{-x-1}$이므로 접점의 $x$좌표를 $\beta$라 하면
$\frac{-e^{-\beta-1}-1-1}{\beta-0} = e^{-\beta-1}$
$-e^{-\beta-1}-2 = \beta e^{-\beta-1}$
$(\beta + 1)e^{-(\beta+1)} = -2$ $\cdots\cdots$ ㉠
한편, 두 직선 $l$, $m$을 직선 $y = x$에 대하여 대칭이동한 직선을 각각 $l’$, $m’$이라 하면 두 직선 $l’$, $m’$의 기울기는 각각 $\frac{1}{1} = 1$, $\frac{1}{e^{-\beta-1}} = e^{\beta+1}$이다.
이때 함수 $y = f(x)$의 그래프와 점 $(1, 0)$에서 이 곡선에 그은 접선은 다음 그림과 같다.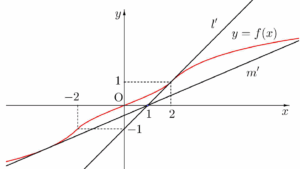 
따라서
$g(m) = \begin{cases} 1 & (m \le 0) \\ 3 & (0 \lt m \lt e^{\beta+1}) \\ 2 & (m = e^{\beta+1}) \\ 1 & (m \gt e^{\beta+1}) \end{cases}$
이므로 함수 $g(m)$이 $m = a$, $m = b$ ($a \lt b$)에서 불연속인 $a$, $b$는
$a = 0$, $b = e^{\beta+1}$
이다.
$b = e^{\beta+1}$에서 $\ln b = \beta+1$이고
㉠에서 $(\beta+1)e^{-(\beta+1)} = \frac{\beta+1}{e^{\beta+1}} = -2$
이므로
$\frac{\ln b}{b} = \frac{\beta+1}{e^{\beta+1}} = -2$
따라서
$\displaystyle g(a) \times \left( \lim_{m \to a+}g(m) \right) + g(b) \times \left( \frac{\ln b}{b} \right)^{2}$
$= 1 \times 3 + 2 \times (-2)^{2} = 11$
수학 영역(기하)
24. 포물선 $y^{2} = 12(x-2)$의 초점과 준선 사이의 거리는? [3점]
① $6$
② $7$
③ $8$
④ $9$
⑤ $10$
25. 좌표공간의 점 $\mathrm{A}(3, \,-\frac{3}{2}, \,-2)$를 $yz$평면에 대하여 대칭이동한 점을 $\mathrm{B}$, 점 $\mathrm{A}$를 원점에 대하여 대칭이동한 점을 $\mathrm{C}$라 할 때, 선분 $\mathrm{BC}$의 길이는? [3점]
① $\sqrt{21}$
② $\sqrt{22}$
③ $\sqrt{23}$
④ $2\sqrt{6}$
⑤ $5$
⑤
점 $\mathrm{A}(3, -\frac{3}{2}, -2)$를 $yz$평면에 대하여 대칭이동한 점 $\mathrm{B}$의 좌표는
$\mathrm{B}(-3, -\frac{3}{2}, -2)$
이고, 점 $\mathrm{A}(3, -\frac{3}{2}, -2)$를 원점에 대하여 대칭이동한 점 $\mathrm{C}$의 좌표는
$\mathrm{C}(-3, \frac{3}{2}, 2)$
따라서 선분 $\mathrm{BC}$의 길이는
$\overline{\mathrm{BC}} = \sqrt{0^{2}+3^{2}+4^{2}} = 5$
26. 양수 $a$에 대하여 두 초점이 $\mathrm{F}$, $\mathrm{F'}$인 쌍곡선 $\dfrac{x^{2}}{a^{2}}-\dfrac{y^{2}}{a^{2}} = -1$ 위의 점 $(a, \sqrt{2}a)$에서의 접선이 $y$축과 만나는 점을 $\mathrm{P}$라 하자. $\overline{\mathrm{PF}}\times \overline{\mathrm{PF'}} = 8$일 때, $a$의 값은? [3점]
① $\sqrt{3}$
② $\frac{4\sqrt{3}}{3}$
③ $\frac{5\sqrt{3}}{3}$
④ $2\sqrt{3}$
⑤ $\frac{7\sqrt{3}}{3}$
②
쌍곡선 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{a^{2}} = -1$ ($a \gt 0$) 위의 점 $(a, \sqrt{2}a)$
에서의 접선의 방정식은
$\frac{ax}{a^{2}}-\frac{\sqrt{2}ay}{a^{2}} = -1$
$x-\sqrt{2}y+a = 0$
위의 직선의 방정식에 $x=0$을 대입하면
$-\sqrt{2}y+a = 0$
$y = \frac{a}{\sqrt{2}}$
즉, 점 $\mathrm{P}$의 좌표는 $(0, \frac{a}{\sqrt{2}})$이다.
한편, 쌍곡선 $\frac{x^{2}}{a^{2}}-\frac{y^{2}}{a^{2}} = -1$의 두 초점 $\mathrm{F}$, $\mathrm{F’}$의 좌표를 각각 $\mathrm{F}(0, c)$, $\mathrm{F’}(0, -c)$ ($c \gt 0$)이라 하면
$c^{2} = a^{2}+a^{2} = 2a^{2}$
$c = \sqrt{2}a$
이므로 $\overline{\mathrm{PF}}\times \overline{\mathrm{PF’}}= 8$에서
$\overline{\mathrm{PF}}\times \overline{\mathrm{PF’}}$
$= |\sqrt{2}a-\frac{a}{\sqrt{2}}| \times |-\sqrt{2}a-\frac{a}{\sqrt{2}}|$
$= 2a^{2}-\frac{a^2}{2}$
$= \frac{3a^2}{2} = 8$
$a^{2} = \frac{16}{3}$
따라서
$a = \frac{4}{\sqrt{3}}$ $= \dfrac{4\sqrt{3}}{3}$
27. 그림과 같이 지름의 길이가 $5$인 두 원 $C_1$, $C_2$를 두 밑면으로 하는 원기둥이 있고, 원 $C_1$ 위의 $\overline{\mathrm{AB}} = 5$인 두 점 $\mathrm{A}$, $\mathrm{B}$와 원 $C_2$ 위의 $\overline{\mathrm{CD}} = 3$인 두 점 $\mathrm{C}$, $\mathrm{D}$에 대하여 $\overline{\mathrm{AD}} = \overline{\mathrm{BC}}$이다. 점 $\mathrm{D}$ 에서 원 $C_1$을 포함하는 평면에 내린 수선의 발을 $\mathrm{H}$라 하자. 사각형 $\mathrm{ABCD}$의 넓이가 삼각형 $\mathrm{ABH}$의 넓이의 $4$배일 때, 이 원기둥의 높이는? [3점]
① $3\sqrt{2}$
② $\sqrt{19}$
③ $2\sqrt{5}$
④ $\sqrt{21}$
⑤ $\sqrt{22}$
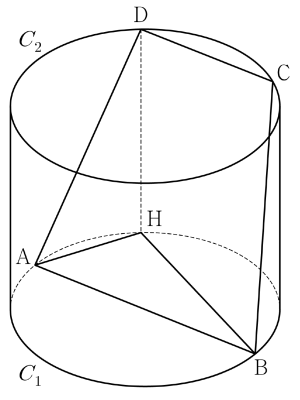
④
점 $\mathrm{D}$에서 원 $C_1$을 포함하는 평면에 내린 수선의 발이 $\mathrm{H}$이므로
$\overline{\mathrm{AD}} = \sqrt{\overline{\mathrm{AH}}^{\,2}+\overline{\mathrm{DH}}^{\,2}}$
점 $\mathrm{C}$에서 원 $C_1$을 포함하는 평면에 내린 수선의 발을 $\mathrm{I}$라 하면
$\overline{\mathrm{BC}} = \sqrt{\overline{\mathrm{BI}}^{\,2}+\overline{\mathrm{CI}}^{\,2}}$
이때 $\overline{\mathrm{AD}} = \overline{\mathrm{BC}}$이고 두 선분 $\mathrm{DH}$, $\mathrm{CI}$는 원기둥의 높이로 서로 같으므로 $\overline{\mathrm{AH}} = \overline{\mathrm{BI}}$이다. 따라서 두 선분 $\mathrm{AB}$, $\mathrm{HI}$는 서로 평행하다.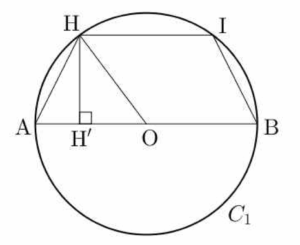 
선분 $\mathrm{AB}$가 원 $C_1$의 지름이므로 선분 $\mathrm{AB}$의 중점을 $\mathrm{O}$라 하면 점 $\mathrm{O}$는 원 $C_1$의 중심이고, 점 $\mathrm{H}$에서 선분 $\mathrm{AB}$에 내린 수선의 발을 $\mathrm{H’}$이라 하면 $\overline{\mathrm{HI}} = \overline{\mathrm{CD}} = 3$이므로
$\overline{\mathrm{OH’}} = \frac{1}{2}\overline{\mathrm{HI}} = \frac{3}{2}$
직각삼각형 $\mathrm{OHH’}$에서
$\overline{\mathrm{HH’}} = \sqrt{\overline{\mathrm{OH}}^{\,2}-\overline{\mathrm{OH’}}^{\,2}}$
$= \sqrt{(\frac{5}{2})^{2}+(\frac{3}{2})^{2}} = 2$
그러므로 삼각형 $\mathrm{ABH}$의 넓이는
$\frac{1}{2}\times \overline{\mathrm{AB}}\times \overline{\mathrm{HH’}} = \frac{1}{2}\times 5\times 2 = 5$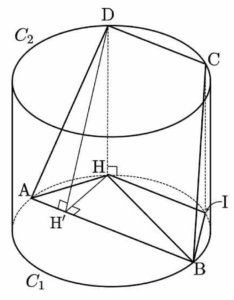
한편, 선분 $\mathrm{DH}$가 원 $C_1$을 포함하는 평면과 수직이고, $\overline{\mathrm{HH’}} \perp \overline{\mathrm{AB}}$이므로 삼수선의 정리에 의하여
$\overline{\mathrm{DH’}} \perp \overline{\mathrm{AB}}$
두 선분 $\mathrm{AB}$, $\mathrm{HI}$는 서로 평행하므로 두 선분 $\mathrm{AB}$, $\mathrm{DC}$는 서로 평행하고 사각형 $\mathrm{ABCD}$는 $\overline{\mathrm{AD}} = \overline{\mathrm{BC}}$인 등변사다리꼴이다.
그러므로 사각형 $\mathrm{ABCD}$의 넓이는
$\frac{1}{2}\times (\overline{\mathrm{AB}}+\overline{\mathrm{DC}})\times \overline{\mathrm{DH’}}$ $= \frac{1}{2}\times 8\times \overline{\mathrm{DH’}} = 4\overline{\mathrm{DH’}}$
사각형 $\mathrm{ABCD}$의 넓이가 삼각형 $\mathrm{ABH}$의 넓이의 $4$배이므로
$4\overline{\mathrm{DH’}} = 4 \times 5$에서 $\overline{\mathrm{DH’}} = 5$
직각삼각형 $\mathrm{DHH’}$에서
$\overline{\mathrm{DH}} = \sqrt{\overline{\mathrm{DH’}}^{\,2}-\overline{\mathrm{HH’}}^{\,2}}$ $= \sqrt{5^{2}-2^{2}} = \sqrt{21}$
따라서 원기둥의 높이는 $\sqrt{21}$이다.
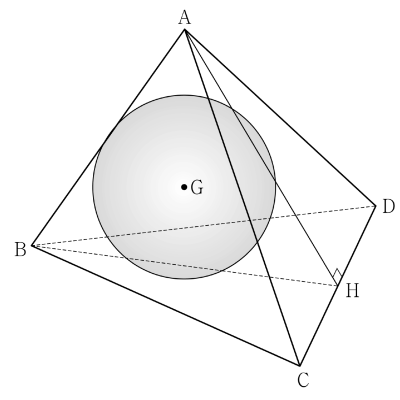
28. 그림과 같이 $\overline{\mathrm{AB}} = \overline{\mathrm{CD}} = 4$, $\overline{\mathrm{BC}} = \overline{\mathrm{BD}} = 2\sqrt{5}$인 사면체 $\mathrm{ABCD}$가 있고, 점 $\mathrm{A}$에서 직선 $\mathrm{CD}$에 내린 수선의 발 $\mathrm{H}$에 대하여 두 평면 $\mathrm{ABH}$와 $\mathrm{BCD}$는 서로 수직이고 $\overline{\mathrm{AH}} = 4$이다. 삼각형 $\mathrm{ABH}$의 무게중심을 $\mathrm{G}$라 하고, 점 $\mathrm{G}$를 중심으로 하고 평면 $\mathrm{ACD}$에 접하는 구를 $S$라 하자. $\angle \mathrm{APG} = \dfrac{\pi}{2}$인 구 $S$ 위의 모든 점 $\mathrm{P}$가 나타내는 도형을 $T$라 할 때, 도형 $T$의 평면 $\mathrm{ABC}$ 위로의 정사영의 넓이는? [4점]
① $\frac{\pi}{7}$
② $\frac{\pi}{6}$
③ $\frac{\pi}{5}$
④ $\frac{\pi}{4}$
⑤ $\frac{\pi}{3}$
④
삼수선의 정리에 의하여 $\overline{\mathrm{BH}} \perp \overline{\mathrm{CD}}$이고, $\overline{\mathrm{BC}} = \overline{\mathrm{BD}}$이므로 $\overline{\mathrm{CH}} = \overline{\mathrm{DH}}$
$\overline{\mathrm{BC}} = 2\sqrt{5}$, $\overline{\mathrm{CH}} = 2$이므로
$\overline{\mathrm{BH}} = \sqrt{(2\sqrt{5})^{2}-2^{2}} = 4$
이때 $\overline{\mathrm{AB}} = 4$, $\overline{\mathrm{AH}} = 4$이므로 삼각형 $\mathrm{ABH}$는 한 변의 길이가 $4$인 정삼각형이다.
$\overline{\mathrm{AH}} \perp \overline{\mathrm{CD}}$, $\overline{\mathrm{BH}} \perp \overline{\mathrm{CD}}$이므로 평면 $\mathrm{ABH}$와 직선 $\mathrm{CD}$는 서로 수직이고, 평면 $\mathrm{ACD}$는 직선 $\mathrm{CD}$를 포함하므로 두 평면 $\mathrm{ABH}$와 $\mathrm{ACD}$는 서로 수직이다.
즉, 삼각형 $\mathrm{ABH}$의 무게중심 $\mathrm{G}$에서 평면 $\mathrm{ACD}$에 내린 수선의 발을 $\mathrm{I}$라 하면 점 $\mathrm{I}$는 선분 $\mathrm{AH}$ 위에 있고, 구 $S$와 평면 $\mathrm{ABH}$가 만나서 생기는 원은 정삼각형 $\mathrm{ABH}$의 내접원이므로
$\overline{\mathrm{AG}} = \frac{2}{3}\times \frac{\sqrt{3}}{2}\times \overline{\mathrm{AB}} = \frac{4\sqrt{3}}{3}$
$\overline{\mathrm{GI}} = \frac{1}{2}\overline{\mathrm{AG}} = \frac{2\sqrt{3}}{3}$
$\overline{\mathrm{AI}} = \frac{1}{2}\overline{\mathrm{AH}} = 2$
이때 $\angle \mathrm{AIG} = \frac{\pi}{2}$이므로 $\angle \mathrm{APG} = \frac{\pi}{2}$인 구 $S$ 위의 모든 점 $\mathrm{P}$가 나타내는 도형 $T$는 점 $\mathrm{I}$를 지나고 직선 $\mathrm{AG}$에 수직인 평면이 구 $S$와 만나서 생기는 원과 같다. 이 원의 반지름의 길이를 $r$이라 하면
$\overline{\mathrm{AI}}\times \overline{\mathrm{GI}} = \overline{\mathrm{AG}}\times r$
$2\times \frac{2\sqrt{3}}{3} = \frac{4\sqrt{3}}{3}r$
$r = 1$
이므로 도형 $T$의 넓이는 $1^{2}\times \pi = \pi$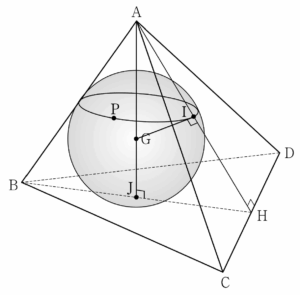
정삼각형 $\mathrm{ABH}$의 내접원이 선분 $\mathrm{BH}$와 만나는 점을 $\mathrm{J}$라 하면 세 점 $\mathrm{A}$, $\mathrm{G}$, $\mathrm{J}$는 한 직선 위에 있고, 두 평면 $\mathrm{ABH}$와 $\mathrm{BCD}$가 서로 수직이므로 평면 $\mathrm{BCD}$와 직선 $\mathrm{AJ}$는 서로 수직이다.
즉, 도형 $T$가 포함된 평면과 평면 $\mathrm{BCD}$가 서로 평행하므로 도형 $T$가 포함된 평면과 평면 $\mathrm{ABC}$가 이루는 예각의 크기는 두 평면 $\mathrm{BCD}$와 $\mathrm{ABC}$가 이루는 예각의 크기와 같다. 이 각의 크기를 $\theta$라 하자.
$\overline{\mathrm{AH}} = 4$, $\overline{\mathrm{CH}} = 2$이고 $\angle \mathrm{AHC} = \frac{\pi}{2}$이므로
$\overline{\mathrm{AC}} = \sqrt{4^{2}+2^{2}} = 2\sqrt{5}$
$\overline{\mathrm{BC}} = \overline{\mathrm{AC}} = 2\sqrt{5}$, $\overline{\mathrm{AB}} = 4$이므로 삼각형 $\mathrm{ABC}$의 넓이를 $k$라 하면
$k = \frac{1}{2}\times \overline{\mathrm{AB}} \times \sqrt{\overline{\mathrm{AC}}^{2}-(\frac{1}{2}\overline{\mathrm{AB}})^{2}}$
$= \frac{1}{2}\times 4 \times \sqrt{(2\sqrt{5})^{2}-2^{2}}$
$= \frac{1}{2}\times 4 \times 4$ $= 8$
삼각형 $\mathrm{ABC}$의 평면 $\mathrm{BCD}$ 위로의 정사영은 삼각형 $\mathrm{JBC}$와 같다. 삼각형 $\mathrm{JBC}$의 넓이를 $k’$이라 하면
$k’ = \frac{1}{2}\times \overline{\mathrm{BJ}} \times \overline{\mathrm{CH}} = \frac{1}{2}\times 2 \times 2 = 2$
따라서 두 평면 $\mathrm{BCD}$와 $\mathrm{ABC}$가 이루는 예각의 크기 $\theta$에 대하여
$\cos \theta = \frac{k’}{k} = \frac{2}{8} = \frac{1}{4}$
이므로 도형 $T$의 평면 $\mathrm{ABC}$ 위로의 정사영의 넓이는
$\pi \cos \theta = \pi \times \frac{1}{4} = \dfrac{\pi}{4}$
29. 그림과 같이 초점이 $\mathrm{F}(p, 0)$ ($p \gt 0$)이고 준선이 $x = -p$인 포물선 위의 점 중 제$1$사분면에 있는 점 $\mathrm{A}$에서 포물선의 준선에 내린 수선의 발을 $\mathrm{H}$라 하고, 두 초점이 $x$축 위에 있고 세 점 $\mathrm{F}$, $\mathrm{A}$, $\mathrm{H}$를 지나는 타원의 $x$좌표가 양수인 초점을 $\mathrm{B}$라 하자. 삼각형 $\mathrm{AHB}$의 둘레의 길이가 $p+27$, 넓이가 $2p+12$일 때, 선분 $\mathrm{HF}$의 길이를 $k$라 하자. $k^{2}$의 값을 구하시오. [4점]
$360$
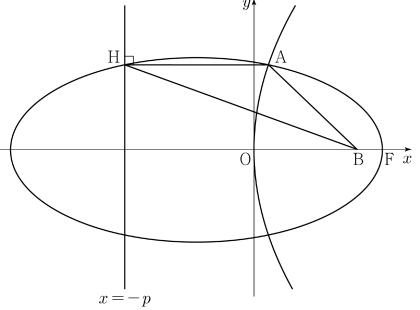
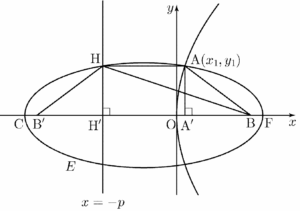세 점 $\mathrm{F}$, $\mathrm{A}$, $\mathrm{H}$를 지나는 타원을 $E$라 하고, 타원 $E$의 점 $\mathrm{B}$가 아닌 초점을 $\mathrm{B}’$, 타원 $E$가 $x$축과 만나는 점 중 $\mathrm{F}$가 아닌 점을 $\mathrm{C}$라 하자.
점 $\mathrm{A}$의 좌표를 $(x_{1}, y_{1})$이라 하면 포물선의 정의에 의하여
$\overline{\mathrm{AF}} = \overline{\mathrm{AH}} = p+x_1$
점 $\mathrm{A}$에서 $x$축에 내린 수선의 발을 $\mathrm{A}’$, 직선 $x = -p$가 $x$축과 만나는 점을 $\mathrm{H}’$이라 하면 타원 $E$는 선분 $\mathrm{A’H’}$의 중점을 지나고 $x$축에 수직인 직선에 대하여 대칭이므로
$\overline{\mathrm{A’F}} = \overline{\mathrm{CH’}} = p-x_1$
타원의 정의에 의하여
$\overline{\mathrm{BH}} + \overline{\mathrm{B’H}} = \overline{\mathrm{CF}}$
$= 2\times \overline{\mathrm{A’F}} + \overline{\mathrm{A’H’}}$
$= 2(p-x_1)+(p+x_1)$
$= 3p-x_1$
이때 $\overline{\mathrm{AB}} = \overline{\mathrm{HB’}}$이므로 삼각형 $\mathrm{AHB}$의 둘레의 길이는
$\overline{\mathrm{AB}}+\overline{\mathrm{BH}}+\overline{\mathrm{AH}}$
$= (\overline{\mathrm{B’H}}+\overline{\mathrm{BH}})+\overline{\mathrm{AH}}$
$= \overline{\mathrm{CF}}+\overline{\mathrm{AH}}$
$= (3p-x_1)+(p+x_1)$
$= 4p$
삼각형 $\mathrm{AHB}$의 둘레의 길이가 $p+27$이므로
$4p = p+27$에서 $p = 9$
즉, 포물선의 방정식은 $y^{2} = 36x$이므로
$y_{1}^{2} = 36x_1$ $\cdots\cdots$ ㉠
한편, 삼각형 $\mathrm{AHB}$의 넓이가 $2p+12 = 30$이므로
$\frac{1}{2}\times \overline{\mathrm{AH}}\times \overline{\mathrm{AA’}} = 30$에서
$\frac{1}{2}\times (9+x_1)\times y_{1} = 30$
즉, $y_{1}(9+x_{1}) = 60$ $\cdots\cdots$ ㉡
㉡의 양변을 제곱하면
$y_{1}^{2}(9+x_{1})^{2} = 3600$
㉠을 위 등식에 대입하면
$36x_{1}(9+x_{1})^{2} = 3600$
$x_{1}^{3}+18x_{1}^{2}+81x_{1}-100 = 0$
$(x_{1}-1)(x_{1}^{2}+19x_{1}+100) = 0$
$x_{1}^{2}+19x_{1}+100 \gt 0$이므로 $x_{1} = 1$
㉡에서 $y_{1} = 6$
직각삼각형 $\mathrm{FHH’}$에서
$\overline{\mathrm{FH’}} = \overline{\mathrm{FA’}}+\overline{\mathrm{A’H’}}$
$= (p-x_1)+(p+x_1)$
$= 2p = 18$
$\overline{\mathrm{AA’}} = y_{1} = 6$
이므로
$\overline{\mathrm{FH}}^{\,2} = \overline{\mathrm{FH’}}^{\,2}+\overline{\mathrm{HH’}}^{\,2}$ $= 18^{2}+6^{2} = 360$
따라서 $k^{2} = 360$
30. 좌표평면에서 길이가 $10\sqrt{2}$인 선분 $\mathrm{AB}$를 지름으로 하는 원 위의 두 점 $\mathrm{P}$, $\mathrm{Q}$가 $$(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}})\cdot(\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{PB}}) = 2|\overrightarrow{\mathrm{PQ}}|^{2}$$ 을 만족시킨다. $|\overrightarrow{\mathrm{PB}}| = 14$일 때, $|\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}}| = \dfrac{q}{p}$이다. $p+q$의 값을 구하시오. (단, $|\overrightarrow{\mathrm{QB}}| \gt 0$이고, $p$와 $q$는 서로소인 자연수이다.) [4점]
$221$
좌표평면에서 선분 $\mathrm{AB}$를 지름으로 하는 원을 $C$라 하자. 선분 $\mathrm{AB}$의 중점을 $\mathrm{O}$라 하면 점 $\mathrm{O}$는 원 $C$의 중심이고, 두 점 $\mathrm{P}$, $\mathrm{Q}$가 원 $C$ 위의 점이고 $\overline{\mathrm{AB}} = 10\sqrt{2}$
이므로
$|\overrightarrow{\mathrm{OA}}| = |\overrightarrow{\mathrm{OB}}| = |\overrightarrow{\mathrm{OP}}| = |\overrightarrow{\mathrm{OQ}}| = \frac{1}{2}\overline{\mathrm{AB}} = 5\sqrt{2}$
$|\overrightarrow{\mathrm{PB}}| = 14$이므로 두 벡터 $\overrightarrow{\mathrm{OB}}$와 $\overrightarrow{\mathrm{OP}}$가 이루는 각의 크기를 $\theta$라 하면 삼각형 $\mathrm{OBP}$에서 코사인법칙에 의하여
$\cos \theta = \dfrac{|\overrightarrow{\mathrm{OB}}|^{2}+|\overrightarrow{\mathrm{OP}}|^{2}-|\overrightarrow{\mathrm{PB}}|^{2}}{2|\overrightarrow{\mathrm{OB}}||\overrightarrow{\mathrm{OP}}|}$
$= \dfrac{(5\sqrt{2})^{2} + (5\sqrt{2})^{2}-14^{2}}{2\times 5\sqrt{2}\times 5\sqrt{2}}$ $= -\dfrac{24}{25}$
$\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OB}} = |\overrightarrow{\mathrm{OP}}||\overrightarrow{\mathrm{OB}}|\cos \theta$
$= 5\sqrt{2}\times 5\sqrt{2}\times (-\frac{24}{25})$ $= -48$
한편
$\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}} = 2\overrightarrow{\mathrm{PO}} = -2\overrightarrow{\mathrm{OP}}$
이고
$\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{PB}}=(\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}})+(\overrightarrow{\mathrm{OB}}-\overrightarrow{\mathrm{OP}})$
$= \overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OQ}}-2\overrightarrow{\mathrm{OP}}$
이므로
$(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}})\cdot(\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{PB}})$
$= -2\overrightarrow{\mathrm{OP}}\cdot(\overrightarrow{\mathrm{OB}}+\overrightarrow{\mathrm{OQ}}-2\overrightarrow{\mathrm{OP}})$
$= -2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OB}}-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}+4|\overrightarrow{\mathrm{OP}}|^{2}$
$= -2 \times (-48)-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}+4\times (5\sqrt{2})^{2}$
$= 296-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}$
이고
$|\overrightarrow{\mathrm{PQ}}|^{2} = |\overrightarrow{\mathrm{OQ}}-\overrightarrow{\mathrm{OP}}|^{2}$
$= |\overrightarrow{\mathrm{OQ}}|^{2}+|\overrightarrow{\mathrm{OP}}|^{2}-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}$
$= (5\sqrt{2})^{2}+(5\sqrt{2})^{2}-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}$
$= 100-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}}$
이므로
$(\overrightarrow{\mathrm{PA}}+\overrightarrow{\mathrm{PB}})\cdot(\overrightarrow{\mathrm{PQ}}+\overrightarrow{\mathrm{PB}}) = 2|\overrightarrow{\mathrm{PQ}}|^{2}$
에서
$296-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}} = 2\times(100-2\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}})$
$\overrightarrow{\mathrm{OP}}\cdot\overrightarrow{\mathrm{OQ}} = -48$
즉, 두 벡터 $\overrightarrow{\mathrm{OP}}$와 $\overrightarrow{\mathrm{OQ}}$가 이루는 각의 크기는 두 벡터 $\overrightarrow{\mathrm{OB}}$와 $\overrightarrow{\mathrm{OP}}$가 이루는 각의 크기 $\theta$와 같다. 이때 $|\overrightarrow{\mathrm{OB}}| \gt 0$이므로 점 $\mathrm{Q}$는 점 $\mathrm{B}$와 일치하지 않고, 따라서 네 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{P}$, $\mathrm{Q}$는 그림과 같다.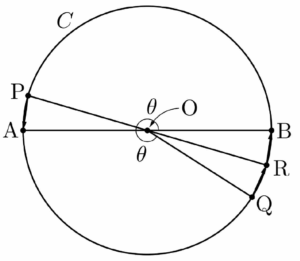 
$\overline{\mathrm{PB}} = 14$, $\overline{\mathrm{AB}} = 10\sqrt{2}$이고 $\angle \mathrm{APB} = \frac{\pi}{2}$이므로
$\overline{\mathrm{PA}} = \sqrt{14^{2}-(10\sqrt{2})^{2}} = 2$
직선 $\mathrm{OP}$가 원 $C$와 만나는 점 중 $\mathrm{P}$가 아닌 점을 $\mathrm{R}$이라 하자.
두 직선 $\mathrm{PA}$, $\mathrm{QR}$이 이루는 각의 크기를 $\alpha$라 하면
$\alpha = \pi-\angle \mathrm{APR}-\angle \mathrm{QRP} = \pi-2\angle \mathrm{APR}$
$= \angle \mathrm{POA} = \pi-\theta$
이고
$|\overrightarrow{\mathrm{QR}}| = |\overrightarrow{\mathrm{RB}}| = |\overrightarrow{\mathrm{PA}}| = 2$
이므로
$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QR}} = |\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{QR}}|\cos (\pi-\alpha)$
$= 2\times 2\times \cos \theta$
$= 2\times 2\times (-\frac{24}{25}) = -\frac{96}{25}$
한편
$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{RB}} = -|\overrightarrow{\mathrm{PA}}||\overrightarrow{\mathrm{RB}}| = -4$
이므로
$\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}} = \overrightarrow{\mathrm{PA}}\cdot(\overrightarrow{\mathrm{QR}}+\overrightarrow{\mathrm{RB}})$
$= \overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QR}}+\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{RB}}$
$= -\frac{96}{25}+(-4) = -\frac{196}{25}$
이고
$|\overrightarrow{\mathrm{PA}}\cdot\overrightarrow{\mathrm{QB}}| = |-\frac{196}{25}| = \dfrac{196}{25}$
따라서 $p = 25$, $q = 196$이므로
$p+q = 25+196 = 221$