25년 9월 평가원


① $\frac{1}{25}$
② $\frac{1}{5}$
③ $1$
④ $5$
⑤ $25$
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
① $2$
② $6$
③ $10$
④ $14$
⑤ $18$
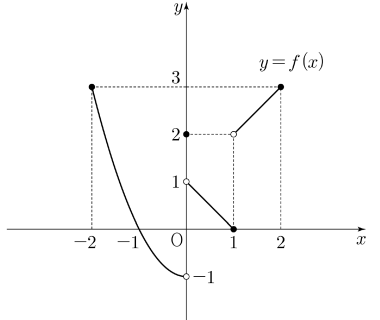
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
① $6$
② $7$
③ $8$
④ $9$
⑤ $10$
① $-\frac{4}{5}$
② $-\frac{3}{5}$
③ $\frac{1}{5}$
④ $\frac{3}{5}$
⑤ $\frac{4}{5}$
⑤
$\cos(\theta-\pi) = \frac{3}{5}$에서
$\cos(\theta-\pi) = \cos(\pi-\theta) = -\cos\theta$
이므로
$-\cos \theta = \frac{3}{5}$, 즉 $\cos \theta = -\frac{3}{5}$
$\cos \theta \lt 0$이고 조건에서 $\tan \theta \lt 0$이므로 $\theta$는 제$2$사분면의 각이다.
이때 $\sin \theta \gt 0$이다.
따라서
$\sin \theta = \sqrt{1-\cos^{2} \theta}$
$= \sqrt{1-(-\frac{3}{5})^{2}}$
$= \sqrt{\frac{16}{25}}$ $= \dfrac{4}{5}$
① $6$
② $7$
③ $8$
④ $9$
⑤ $10$
① $2$
② $4$
③ $8$
④ $16$
⑤ $32$
③
$\log_{\sqrt{2}}a + \log_{2}b = 2$에서
$\log_{\sqrt{2}}a + \log_{2}b$ $= 2\log_{2}a + \log_{2}b$
$= \log_{2}a^{2} + \log_{2}b = \log_{2}a^{2}b$ $= 2$
이므로
$a^{2}b = 2^{2}$ $\cdots\cdots$ ㉠
$\log_{2}a + \log_{2}b^{2} = 7$에서
$\log_{2}a + \log_{2}b^{2} = \log_{2}ab^{2} = 7$
이므로
$ab^{2} = 2^{7}$ $\cdots\cdots$ ㉡
㉠, ㉡을 변끼리 곱하면
$a^{3}b^{3} = 2^{2}\times2^{7} = 2^{9}$
이고 $a$, $b$가 양의 실수이므로
$(ab)^{3} = (2^{3})^{3}$에서 $ab = 2^{3} = 8$
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
②
$F(x)$가 $f(x)$의 한 부정적분이므로
$F'(x) = f(x)$이고,
$G(x)$가 $2f(x)+1$의 한 부정적분이므로
$G'(x) = 2f(x)+1$
이때 $H(x) = G(x)-2F(x)$라 하면
$H'(x) = G'(x)-2F'(x)$ $= 2f(x)+1-2f(x) = 1$이므로
$H(x) = x + C$ (단, $C$는 적분상수)
한편, $G(3) = 2F(3)$에서
$H(3) = G(3)-2F(3) = 0$이므로 $3+C=0$
즉 $C = -3$이므로 $H(x) = x-3$
따라서 $G(5)-2F(5) = H(5)$ $= 5-3 = 2$
① $61$
② $63$
③ $65$
④ $67$
⑤ $69$
③
등비수열 $\{ a_n \}$의 공비를 $r$이라 하면 수열 $\{ a_n \}$의 모든 항이 양수이므로 $r \gt 0$이다.
$a_2 = 1$에서 $a_{1}r = 1$ $\cdots\cdots$ ㉠
$\displaystyle \sum_{k=1}^{6}(-1)^{k}S_{k} = 21$에서
$-S_{1}+S_{2}-S_{3}+S_{4}-S_{5}+S_{6} = 21$
$(-S_{1}+S_{2})+(-S_{3}+S_{4})+(-S_{5}+S_{6}) = 21$
$a_{2}+a_{4}+a_{6} = 21$, $a_{2}+a_{2}r^{2}+a_{2}r^{4} = 21$
$a_{2} = 1$이므로 $1+r^{2}+r^{4} = 21$
$r^{4}+r^{2}-20 = 0$, $(r^{2}+5)(r^{2}-4) = 0$
$(r^{2}+5)(r+2)(r-2) = 0$
$r \gt 0$이므로 $r = 2$
㉠에서 $2a_{1} = 1$이므로 $a_{1} = \frac{1}{2}$
따라서 $S_{2} + S_{7}$ $= \dfrac{\frac{1}{2}\times(2^{2}-1)}{2-1} + \dfrac{\frac{1}{2}\times(2^{7}-1)}{2-1}$
$= \frac{3}{2}+\frac{127}{2}$ $= \dfrac{130}{2} = 65$
ㄱ. 시각 $t = 1$일 때 점 $\mathrm{P}$의 운동 방향이 바뀐다.
ㄴ. 시각 $t = 1$일 때 점 $\mathrm{P}$의 위치는 $3$이다.
ㄷ. 시각 $t = 0$에서 $t = 2$까지 점 $\mathrm{P}$가 움직인 거리는 $4$이다.
① ㄱ
② ㄱ, ㄴ
③ ㄱ, ㄷ
④ ㄴ, ㄷ
⑤ ㄱ, ㄴ, ㄷ
⑤
ㄱ.
$v(t) = 3t^{2}-10t+7 = (t-1)(3t-7)$이므로
$v(t) = 0$에서
$t = 1$ 또는 $t = \frac{7}{3}$
$0 \lt t \lt 1$일 때, $v(t) \gt 0$이고
$1 \lt t \lt \frac{7}{3}$일 때, $v(t) \lt 0$이므로
시각 $t = 1$일 때 점 $\mathrm{P}$의 운동 방향이 바뀐다. (참)
ㄴ.
시각 $t$ ($t \ge 0$)일 때 점 $\mathrm{P}$의 위치를 $x(t)$라 하자.
$t = 0$일 때 점 $\mathrm{P}$의 위치가 원점이므로
$x(1) = \int_{0}^{1}v(t)dt = \int_{0}^{1}(3t^{2}-10t+7)dt$
$= \bigg[\, t^{3}-5t^{2}+7t\,\bigg]_{0}^{1}$
$= 1-5+7 = 3$ (참)
ㄷ.
$0 \lt t \lt 1$일 때, $v(t) \gt 0$이고
$1 \lt t \lt 2$일 때, $v(t) \lt 0$이므로
시각 $t = 0$에서 $t=2$ 까지 점 $\mathrm{P}$가 움직인 거리를 $s$라 하면
$s = \int_{0}^{2}|\,v(t)\,|dt = \int_{0}^{2}|\,3t^{2}-10t+7\,|dt$
$= \int_{0}^{1}(3t^{2}-10t+7)dt + \int_{1}^{2}\{-(3t^{2}-10t+7)\}dt$
$= \bigg[\, t^{3}-5t^{2}+7t\,\bigg]_{0}^{1}-\bigg[\, t^{3}-5t^{2}+7t\,\bigg]_{1}^{2}$
$= 3-\{(8-20+14)-3\} = 4$ (참)
이상에서 옳은 것은 ㄱ, ㄴ, ㄷ이다.
① $2^{\frac{9}{4}}$
② $2^{\frac{23}{8}}$
③ $2^{\frac{7}{2}}$
④ $2^{\frac{33}{8}}$
⑤ $2^{\frac{19}{4}}$
①
두 점 $\mathrm{A}$, $\mathrm{B}$의 좌표는 각각 $\mathrm{A}(t, a^{t})$, $\mathrm{B}(2t, a^{2t})$이고 점 $\mathrm{C}$의 좌표는 $\mathrm{C}(2t, 0)$이다.
또한 삼각형 $\mathrm{ACB}$는 $\overline{\mathrm{AB}} = \overline{\mathrm{AC}}$인 이등변 삼각형이므로 점 $\mathrm{A}$에서 선분 $\mathrm{BC}$에 내린 수선의 발 $\mathrm{H}$는 선분 $\mathrm{BC}$의 중점이다.
이때 $\mathrm{H}(2t, a^{t})$이므로 $2a^{t} = a^{2t}$
$a^{t}=2$ $\cdots\cdots$ ㉠
이때 삼각형 $\mathrm{ACB}$의 넓이가 $8$이므로
$\frac{1}{2}\times(2t-t)\times a^{2t} = 8$
$t\times (a^{t})^{2} = 16$
㉠에서 $a^{t} = 2$이므로 $t\times 2^{2} = 16$, $t = 4$
즉 $a^{4} = 2$이고 $a \gt 1$이므로 $a = 2^{\frac{1}{4}}$
따라서 $a \times t = 2^{\frac{1}{4}} \times 4 = 2^{\frac{1}{4}+2}$ $= 2^{\frac{9}{4}}$
13. 함수 $f(x) = x^{2}+6x+12$에 대하여 다음 조건을 만족시키는 모든 정수 $k$의 개수는? [4점]
① $5$
② $6$
③ $7$
④ $8$
⑤ $9$
④
$f(x) = x^{2}+6x+12 = (x+3)^{2}+3 \gt 0$
모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a}\frac{x^2}{(f(x))^{2}-k(x+2)f(x)}$의 값이 존재하는 경우를 다음 두 가지 경우로 나누어 조사하자.
(ⅰ) 모든 실수 $a$에 대하여 $\displaystyle \lim_{x \to a}\{(f(x))^{2}-k(x+2)f(x)\} \ne 0$인 경 우
$\displaystyle \lim_{x \to a}\{(f(x))^{2}-k(x+2)f(x)\} = (f(a))^{2}-k(a+2)f(a)$
$= f(a)\{f(a)-k(a+2)\}$에서
$f(a) \gt 0$이므로 $f(a) \ne k(a+2)$
$x$에 대한 방정식 $f(x) = k(x+2)$의 실근이 존재하지 않아야 하므로 이차방정식 $x^{2}+6x+12 = kx+2k$
즉, $x^{2}+(6-k)x+12-2k = 0$의 판별식을 $D$라 하면
$D = (6-k)^{2}-4(12-2k) \lt 0$이어야 한다.
$k^{2}-4k-12 \lt 0$, $(k+2)(k-6) \lt 0$
$-2 \lt k \lt 6$
(ⅱ) $\displaystyle \lim_{x \to a}\{(f(x))^{2}-k(x+2)f(x)\} = 0$인 실수 $a$가 존재하는 경우
$\displaystyle \lim_{x \to a}x^{2} = 0$이어야 하므로 $a^{2} = 0$, $a=0$
$\displaystyle \lim_{x \to 0}\{(f(x))^{2}-k(x+2)f(x)\} = (f(0))^{2}-2kf(0)$
$= f(0)(f(0)-2k) = 0$
$f(0) \gt 0$이므로 $f(0) = 2k$
즉, $12 = 2k$에서 $k = 6$
이때, $\displaystyle \lim_{x \to 0}\frac{x^2}{(f(x))^{2}-6(x+2)f(x)}$
$= \displaystyle \lim_{x \to 0}\frac{x^2}{f(x)(f(x)-6x-12)}$
$= \displaystyle \lim_{x \to 0}\frac{x^2}{(x^{2}+6x+12)x^{2}}$
$= \displaystyle \lim_{x \to 0}\frac{1}{x^{2}+6x+12}$
$= \frac{1}{12}$
이므로 조건을 만족시킨다.
(ⅰ), (ⅱ)에서 $-2 \lt k \le 6$이므로 조건을 만족시키는 모든 정수 $k$는 $-1$, $0$, $1$, $\cdots$, $6$이고 그 개수는 $8$이다.
① $\frac{4\sqrt{3}}{3}$
② $\frac{13\sqrt{3}}{9}$
③ $\frac{14\sqrt{3}}{9}$
④ $\frac{5\sqrt{3}}{3}$
⑤ $\frac{16\sqrt{3}}{9}$
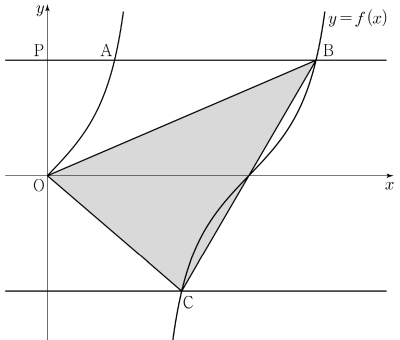
③
함수 $y = f(x)$의 그래프와 $x$축이 만나는 점 중 원점이 아닌 점을 $\mathrm{D}$라 하자.
함수 $y = \tan \frac{x}{k}$의 주기가 $\dfrac{\pi}{\frac{1}{k}} = k \pi$이므로
$\overline{\mathrm{AB}} = \overline{\mathrm{OD}} = k \pi$
$\overline{\mathrm{AB}} = 3\overline{\mathrm{PA}}$이므로 $\overline{\mathrm{PA}} = \frac{1}{3} \times \overline{\mathrm{AB}} = \frac{k \pi}{3}$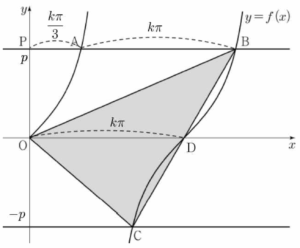 점 $\mathrm{A}$의 좌표가 $(\frac{k \pi}{3}, p)$이고 점 $\mathrm{A}$가 함수 $f(x) = \tan \frac{x}{k}$의 그래프 위의 점이므로
점 $\mathrm{A}$의 좌표가 $(\frac{k \pi}{3}, p)$이고 점 $\mathrm{A}$가 함수 $f(x) = \tan \frac{x}{k}$의 그래프 위의 점이므로
$p = \tan (\frac{1}{k} \times \frac{k \pi}{3}) = \tan \frac{\pi}{3} = \sqrt{3}$
삼각형 $\mathrm{OCB}$의 넓이가 $\frac{5 \pi}{3}$이고
(삼각형 $\mathrm{OCB}$의 넓이)
$=\,$(삼각형 $\mathrm{ODB}$의 넓이)$\,+\,$(삼각형 $\mathrm{OCD}$의 넓이)
$= \frac{1}{2} \times \overline{\mathrm{OD}} \times p + \frac{1}{2} \times \overline{\mathrm{OD}} \times p$
$= 2 \times \frac{1}{2} \times k \pi \times \sqrt{3}$ $= \sqrt{3} k \pi$
이므로
$\sqrt{3} k \pi = \frac{5 \pi}{3}$
$k = \frac{5}{3\sqrt{3}} = \frac{5\sqrt{3}}{9}$
따라서
$k + p = \frac{5\sqrt{3}}{9} + \sqrt{3} = \dfrac{14\sqrt{3}}{9}$
$f(6) \times g(2) \lt 0$일 때, $f(8)$의 값은? [4점]
① $16$
② $22$
③ $28$
④ $34$
⑤ $40$
⑤
$g(x) = \int_{0}^{x}(|\,f(t)\,|-|\,t\,|)dt$에서 $g'(x) = |\,f(x)\,|-|\,x\,|$
이때 조건 (나)에서 $g'(2) = 0$, $g'(6) = 0$이므로
$|\,f(2)\,| = 2$, $|\,f(6)\,| = 6$
즉, $f(2) = -2$ 또는 $f(2) = 2$이고 $f(6) = -6$ 또는 $f(6) = 6$
또한 주어진 조건에서 $f(0) = 0$이다.
그리고 조건 (가)에 의하여 방정식 $f(x) = x$ 또는 $f(x) = -x$의 서로 다른 실근의 개수가 $4$이다.
(ⅰ) $f(0) = 0$, $f(2) = 2$, $f(6) = 6$일 때
방정식 $f(x) = x$가 $x = 0$, $x = 2$, $x = 6$의 세 실근을 가지므로
$f(x)-x = kx(x-2)(x-6)$
$f(x) = kx(x-2)(x-6)+x$ ($k$는 양의 상수)라 하자.
이때 방정식 $f(x) = -x$가 $0$이 아닌 한 실근을 가져야 조건 (가)를 만족시키므로
$kx(x-2)(x-6)+x = -x$, $x\{ k(x-2)(x-6)+2\} = 0$
$x(kx^{2}-8kx+12k+2) = 0$
에서 $x$에 대한 이차방정식 $kx^{2}-8kx+12k+2 = 0$이 중근을 가져야 한다.
따라서 이 이차방정식의 판별식을 $D$라 하면
$\frac{D}{4} = (-4k)^{2}-k(12k+2) = 4k^{2}-2k = 2k(2k-1) = 0$에서
$k \gt 0$이므로 $k = \frac{1}{2}$
$kx^{2}-8kx+12k+2 = 0$에서 $\frac{1}{2}x^{2}-4x+8 = 0$, $x^{2}-8x+16 = 0$
$(x-4)^{2} = 0$, $x = 4$
따라서 함수 $f(x) = \frac{1}{2}x(x-2)(x-6)+x$의 그래프는 그림과 같고 $g(2) = \int_{0}^{2}(|\,f(t)\,|-|\,t\,|)dt \gt 0$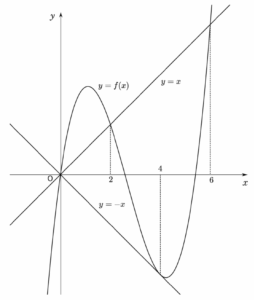 이때 $f(6) \times g(2) \lt 0$에서 $g(2) \lt 0$이므로 모순이다.
이때 $f(6) \times g(2) \lt 0$에서 $g(2) \lt 0$이므로 모순이다.
(ⅱ) $f(0) = 0$, $f(2) = 2$, $f(6) = -6$일 때
최고차항의 계수가 양수인 삼차함수 $y = f(x)$의 그래프는 $f(6) = -6$이므로 $x \gt 6$일 때 직선 $y = x$와 반드시 교점을 갖는다.
따라서 조건 (가)를 만족시키기 위해서는 $y = f(x)$의 그래프와 직선 $y = -x$가 $x = 6$에서 접해야 한다.
그러나 조건 (나)에서 함수 $g(x)$가 $x = 6$에서 극값을 가지므로 모순이다.
(ⅲ) $f(0) = 0$, $f(2) = -2$, $f(6) = -6$일 때
방정식 $f(x) = -x$에서 $x = 0$, $x = 2$, $x = 6$의 세 실근을 가지므로 $f(x)+x = kx(x-2)(x-6)$
$f(x) = kx(x-2)(x-6)-x$ ($k$는 양의 상수)라 하자.
이때 $f(x) = x$가 $0$이 아닌 한 실근을 가져야 조건 (가)를 만족시키므로
$kx(x-2)(x-6)-x = x$, $x\{k(x-2)(x-6)-2\} = 0$
$x(kx^{2}-8kx+12k-2) = 0$에서 $x$에 대한 이차방정식 $kx^{2}-8kx+12k-2 = 0$이 중근을 가져야 한다.
따라서 이 이차방정식의 판별식을 라 $D$하면
$\frac{D}{4} = (-4k)^{2}-k(12k-2) = 4k^{2}+2k = 2k(2k+1) = 0$에서
$k = 0$ 또는 $k = -\frac{1}{2}$
그런데 $k \gt 0$이므로 모순이다.
(ⅳ) $f(0) = 0$, $f(2) = -2$, $f(6) = 6$일 때
$f(x) = kx^{3}+px^{2}+qx$ ($k$는 양의 상수, $p$, $q$는 상수)라 하자.
이때
$f(2) = 8k + 4p + 2q = -2$ $\cdots\cdots$ ㉠
$f(6) = 216k + 36p + 6q = 6$ $\cdots\cdots$ ㉡
이므로 $2 \lt x \lt 6$에서 $f(x) = 0$을 만족시키는 $x$의 값이 반드시 존재한다.
이때, $f(6) \times g(2) \lt 0$에서 $g(2) \lt 0$이어야 하고, 조건 (나)에서 함수 $g(x)$는 $x=2$에서 극값을 가지므로 $2 \lt x \lt 6$에서 방정식 $|f(x)| = x$를 만족시키는 $x$의 값이 반드시 존재한다.
즉, $x \lt 0$에서 방정식 $f(x) = -x$는 근을 갖지 않아야 조건 (가)를 만족시키므로 함수 $y = f(x)$의 그래프는 직선 $y = x$와 $x=0$에서 접해야 한다.
이때 $f'(x) = 3kx^{2}+2px+q$이므로 $f'(0) = q = 1$
㉠, ㉡에 대입하면 $k = \frac{1}{4}$, $p = -\frac{3}{2}$
이므로
$f(x) = \frac{1}{4}x^{3}-\frac{3}{2}x^{2}+x$
이상에서 $f(x) = \frac{1}{4}x^{3}-\frac{3}{2}x^{2}+x$이므로
$f(8) = \frac{1}{4} \times 8^{3}-\frac{3}{2} \times 8^{2}+8 = 40$
[참고]
주어진 조건을 만족시키는 함수 $y = f(x)$의 그래프는 그림과 같다.

$10$
$f(x) = 2x^{3}-3ax^{2}+5a$에서
$f'(x) = 6x^{2}-6ax = 6x(x-a)$
이때 함수 $f(x)$는 극솟값을 가지므로 $a \ne 0$이다.
(ⅰ) $a \lt 0$일 때
함수 $f(x)$는 $x = 0$에서 극솟값을 가지므로 $f(0) = 5a = a$, $a = 0$
$a \lt 0$이므로 모순이다.
(ⅱ) $a \gt 0$일 때
함수 $f(x)$는 $x = a$에서 극솟값을 가지므로
$f(a) = 2a^{3}-3a^{3}+5a = -a^{3}+5a = a$
$a^{3}-4a = 0$, $a(a+2)(a-2) = 0$
이때 $a \gt 0$이므로 $a = 2$
(ⅰ), (ⅱ)에서 $f(x) = 2x^{3}-6x^{2}+10$이고 함수 $f(x)$는 $x = 0$에서 극댓값을 가지므로 구하는 극댓값은
$f(0) = 10$
20. 그림과 같이 사각형 $\mathrm{ABCD}$가 한 원에 내접하고 $\overline{\mathrm{AB}} : \overline{\mathrm{CD}} = 1 : 3$, $\overline{\mathrm{BC}} \lt \overline{\mathrm{AD}}$일 때, 직선 $\mathrm{AB}$와 직선 $\mathrm{CD}$가 만나는 점을 $\mathrm{P}$라 하자.
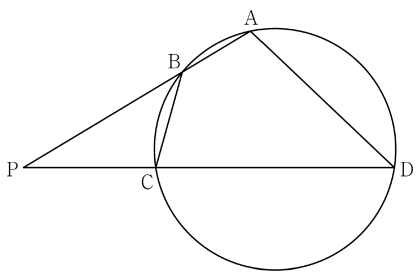
$\angle \mathrm{BPC} = \theta$라 할 때, $\overline{\mathrm{PB}} : \overline{\mathrm{PC}} : \overline{\mathrm{BC}} = 7 : 5 : \sqrt{14}$이므로 삼각형 $\mathrm{BPC}$에서 코사인법칙에 의하여 $\cos \theta = \frac{6}{7}$이다.
$\overline{\mathrm{PB}} : \overline{\mathrm{PC}} = 7 : 5$에서 $\overline{\mathrm{PB}} = 7k$, $\overline{\mathrm{PC}} = 5k$,
$\overline{\mathrm{AB}} : \overline{\mathrm{CD}} = 1 : 3$에서 $\overline{\mathrm{AB}} = l$, $\overline{\mathrm{CD}} = 3l$이라 하자.
원의 성질에 의하여 삼각형 $\mathrm{BPC}$와 삼각형 $\mathrm{DPA}$가 서로 닮음이므로 $\overline{\mathrm{PB}} : \overline{\mathrm{PC}} = \overline{\mathrm{PD}} : \overline{\mathrm{PA}}$이고, $l = \fbox{ $\textbf{(가)}$ } \times k$이다.
삼각형 $\mathrm{BPC}$와 삼각형 $\mathrm{DPA}$의 닮음비가 $1 : \fbox{ $\textbf{(나)}$ }$이므로
$\overline{\mathrm{BC}} = \dfrac{1}{\fbox{ $\textbf{(나)}$ }} \times \overline{\mathrm{AD}}$이다.
따라서 삼각형 $\mathrm{BPC}$의 외접원의 반지름의 길이를 $R$이라 할 때, 삼각형 $\mathrm{BPC}$에서 사인법칙에 의하여 $R = \fbox{ $\textbf{(다)}$ }$이다.
위의 (가), (나), (다)에 알맞은 수를 각각 $p$, $q$, $r$이라 할 때, $p+q+r$의 값을 구하시오. [4점]
$12$
$\angle \mathrm{BPC} = \theta$라 할 때,
$\overline{\mathrm{PB}} : \overline{\mathrm{PC}} : \overline{\mathrm{BC}} = 7 : 5 : \sqrt{14}$이므로
삼각형 $\mathrm{BPC}$에서 코사인법칙에 의하여 $\cos \theta = \frac{6}{7}$이다.
$\overline{\mathrm{PB}} : \overline{\mathrm{PC}} = 7 : 5$에서 $\overline{\mathrm{PB}} = 7k$, $\overline{\mathrm{PC}} = 5k$
$\overline{\mathrm{AB}} : \overline{\mathrm{CD}} = 1 : 3$에서 $\overline{\mathrm{AB}} = l$, $\overline{\mathrm{CD}} = 3l$이라 하자.
원의 성질에 의하여 삼각형 $\mathrm{BPC}$와 삼각형 $\mathrm{DPA}$가 서로 닮음이므로 $\overline{\mathrm{PB}} : \overline{\mathrm{PC}} = \overline{\mathrm{PD}} : \overline{\mathrm{PA}}$이고,
$\overline{\mathrm{PD}} = \overline{\mathrm{PC}} + \overline{\mathrm{CD}} = 5k + 3l$,
$\overline{\mathrm{PA}} = \overline{\mathrm{PB}} + \overline{\mathrm{AB}} = 7k + l$이므로
$\overline{\mathrm{PB}} : \overline{\mathrm{PC}} = \overline{\mathrm{PD}} : \overline{\mathrm{PA}}$에서
$7 : 5 = (5k+3l) : (7k+l)$, $5(5k+3l) = 7(7k+l)$
$l =\,\fbox{$\,3 \:$}\times k$이다.
$\overline{\mathrm{PD}} = 5k+3l = 14k$이므로
$\overline{\mathrm{PB}} : \overline{\mathrm{PD}} = 7k : 14k = 1 : 2$
즉, 삼각형 $\mathrm{BPC}$와 삼각형 $\mathrm{DPA}$의 닮음비가 $1 : \fbox{$\:2 \:$}$이므로
$\overline{\mathrm{BC}} = \dfrac{1}{\fbox{$\:2 \:$}} \times \overline{\mathrm{AD}}$이다.
$\cos \theta = \frac{6}{7}$에서
$\sin \theta = \sqrt{1-\cos^{2}\theta}$ $= \sqrt{1-(\frac{6}{7})^{2}} = \frac{\sqrt{13}}{7}$
한편,
$\overline{\mathrm{BC}} = \frac{1}{2}\overline{\mathrm{AD}}$ $= \frac{1}{2}\times 4\sqrt{13} = 2\sqrt{13}$
따라서 삼각형 $\mathrm{BPC}$의 외접원의 반지름의 길이를 $R$이라 할 때, 삼각형 $\mathrm{BPC}$에서 사인법칙에 의하여
$R = \dfrac{\overline{\mathrm{BC}}}{2\sin \theta}$ $= \dfrac{2\sqrt{13}}{2 \times \frac{\sqrt{13}}{7}}$ $= \fbox{$\:7 \:$}$
따라서 $p = 3$, $q = 2$, $r = 7$이므로
$p+q+r = 3+2+7$ $= 12$
$296$
$f(x)$는 최고차항의 계수가 $1$인 삼차함수이므로
$f(x) = x^{3}+ax^{2}+bx+c$ (단, $a$, $b$, $c$는 상수)
로 놓으면
$f'(x) = 3x^{2}+2ax+b$
주어진 조건에서 $0$이 아닌 모든 실수 $x$에 대하여
$\dfrac{f'(x)}{2}+x^{2}-2 \le \dfrac{f(2x)-f(0)}{2x} \le x^{4}$이므로
$\dfrac{3x^{2}+2ax+b}{2}+x^{2}-2 \le \dfrac{8x^{3}+4ax^{2}+2bx}{2x} \le x^{4}$
$5x^{2}+2ax+b-4 \le 8x^{2}+4ax+2b \le 2x^{4}$
즉, $-3x^{2}-4 \le 2ax+b \le x^{4}-4x^{2}$ $\cdots\cdots$ ㉠
이때 $g(x) = -3x^{2}-4$, $h(x) = x^{4}-4x^{2}$이라 하면 곡선 $y = g(x)$는 꼭짓점의 좌표가 $(0, -4)$인 위로 볼록한 포물선이다.
또, $h'(x) = 4x^{3}-8x = 4x(x^{2}-2) = 0$에서
$x = 0$, $x = \sqrt{2}$, $x = -\sqrt{2}$이므로 함수 $h(x)$의 증가와 감소를 표로
나타내면 다음과 같다.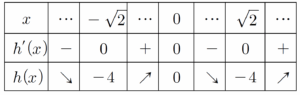
즉, 두 함수 $y = g(x)$, $y = h(x)$의 그래프는 다음과 같다. 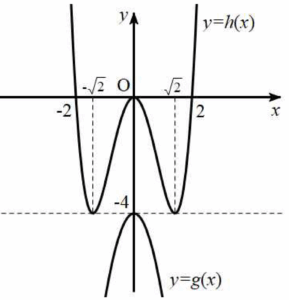 그러므로 부등식 ㉠을 만족시키려면 직선 $y = 2ax+b$가 $y = -4$이어야 한다.
그러므로 부등식 ㉠을 만족시키려면 직선 $y = 2ax+b$가 $y = -4$이어야 한다.
즉, $a = 0$, $b = -4$이므로 $f'(x) = 3x^{2}-4$
따라서 $f'(10) = 3 \times 10^{2}-4 = 296$
$73$
두 점 $\mathrm{A}$, $\mathrm{B}$가 곡선 $y = \log_{2}x$ 위의 점이므로 두 점 $\mathrm{A}$, $\mathrm{B}$를
$\mathrm{A}(a, \log_{2}a)$, $\mathrm{B}(b, \log_{2}b)$ (단, $a$, $b$는 양수)로 놓을 수 있다.
조건 (가)에서
(직선 $\mathrm{AP}$의 $y$절편)$\,-\,$(직선 $\mathrm{BQ}$의 $y$절편) $\,= \frac{13}{2}$
이므로 $a \gt b$이다.
점 $\mathrm{A}$에서 직선 $y = x$에 내린 수선의 발이 점 $\mathrm{P}$이므로 직선 $\mathrm{AP}$의 기울기는 $-1$이다.
이때, 직선 $\mathrm{AP}$의 방정식은 $y-\log_{2}a = -(x-a)$
즉, $y = -x+a+\log_{2}a$이므로 직선 $\mathrm{AP}$의 $y$절편은 $a+\log_{2}a$이다.
점 $\mathrm{B}$를 직선 $y=x$에 대하여 대칭이동한 점이 $\mathrm{Q}$이므로 점 $\mathrm{Q}$의 좌표는 $(\log_{2}b, b)$이고, 직선 $\mathrm{BQ}$의 기울기는 $-1$이다.
이때, 직선 $\mathrm{BQ}$의 방정식은 $y-\log_{2}b = -(x-b)$
즉, $y = -x+b+\log_{2}b$이므로 직선 $\mathrm{BQ}$의 $y$절편은 $b+\log_{2}b$이다.
조건 (가)에 의하여
$(a+\log_{2}a)-(b+\log_{2}b) = \frac{13}{2}$이므로
$(a-b)+(\log_{2}a-\log_{2}b) = \frac{13}{2}$ $\cdots\cdot$ ㉠
한편, 조건 (나)에서 직선 $\mathrm{AB}$의 기울기가 $\frac{6}{7}$이므로
$\frac{\log_{2}a-\log_{2}b}{a-b} = \frac{6}{7}$
$\log_{2}a-\log_{2}b = \frac{6}{7}(a-b)$ $\cdots\cdots$ ㉡
㉡을 ㉠에 대입하면 $(a-b)+\frac{6}{7}(a-b) = \frac{13}{2}$
$\frac{13}{7}(a-b) = \frac{13}{2}$
$a-b = \frac{7}{2}$ $\cdots\cdots$ ㉢
㉢을 ㉡에 대입하면 $\log_{2}a-\log_{2}b = \frac{6}{7}\times\frac{7}{2}$
$\log_{2}\frac{a}{b} = 3$, $\frac{a}{b} = 2^3$
$a = 8b$ $\cdots\cdots$ ㉣
㉣을 ㉢에 대입하면 $8b-b= \frac{7}{2}$, $7b = \frac{7}{2}$
$b = \frac{1}{2}$
$b = \frac{1}{2}$을 ㉣에 대입하면 $a = 8 \times \frac{1}{2} = 4$
직선 $\mathrm{AP}$의 방정식은 $y = -x+6$이고, 직선 $\mathrm{AP}$와 직선 $y=x$의 교점이 점 $\mathrm{P}$이므로
$-x+6 = x$에서 $x=3$
즉 점 $\mathrm{P}$의 좌표는 $(3, 3)$
한편, 세 점 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{Q}$는
$\mathrm{A}(4, 2)$, $\mathrm{B}(\frac{1}{2}, -1)$, $\mathrm{Q}(-1, \frac{1}{2})$
선분 $\mathrm{BQ}$의 중점을 $\mathrm{M}$이라 하면 $\mathrm{M}(-\frac{1}{4}, -\frac{1}{4})$이고 $\angle \mathrm{PMB} = 90^{\circ}$이다.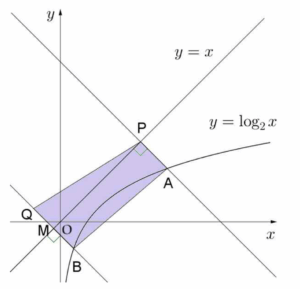 이때
이때
$\overline{\mathrm{AP}} = \sqrt{(3-4)^{2}+(3-2)^{2}} = \sqrt{2}$,
$\overline{\mathrm{BQ}} = \sqrt{(-1-\frac{1}{2})^{2}+(\frac{1}{2}-(-1))^{2}} = \frac{3\sqrt{2}}{2}$,
$\overline{\mathrm{PM}} = \sqrt{(-\frac{1}{4}-3)^{2}+(-\frac{1}{4}-3)^{2}} = \frac{13\sqrt{2}}{4}$
이므로 사각형 $\mathrm{APQB}$의 넓이를 $S$라 하면
$S = \frac{1}{2} \times (\overline{\mathrm{AP}}+\overline{\mathrm{BQ}})\times\overline{\mathrm{PM}}$
$= \frac{1}{2} \times (\sqrt{2}+\frac{3\sqrt{2}}{2})\times\frac{13\sqrt{2}}{4}$
$= \frac{65}{8}$
따라서 $p = 8$, $q = 65$이므로
$p+q = 8 + 65 = 73$
수학 영역(확률과 통계)

① $72$
② $75$
③ $78$
④ $81$
⑤ $84$
① $\frac{1}{3}$
② $\frac{3}{8}$
③ $\frac{5}{12}$
④ $\frac{11}{24}$
⑤ $\frac{1}{2}$
① $\frac{1}{4}$
② $\frac{15}{56}$
③ $\frac{2}{7}$
④ $\frac{17}{56}$
⑤ $\frac{9}{28}$
⑤
$8$명의 학생 중 임의로$5$명의 학생을 선택하는 경우의 수는
${}_{8}\mathrm{C}_{5} = {}_{8}\mathrm{C}_{3} = \frac{8 \times 7 \times 6}{3 \times 2 \times 1} = 56$
선택된 $2$학년 학생 수와 선택된 $3$학년 학생 수가 서로 같은 경우는 $1$학년 학생 $1$명을 선택하고 $2$학년과 $3$학년 학생을 각각 $2$명씩 선택하는 경우이므로 이 경우의 수는
$1 \times {}_{3}\mathrm{C}_{2} \times {}_{4}\mathrm{C}_{2}$ $= 1 \times 3 \times \frac{4 \times 3}{2 \times 1} = 18$
따라서 구하는 확률은 $\frac{18}{56} = \dfrac{9}{28}$
① $0.47$
② $0.49$
③ $0.51$
④ $0.53$
⑤ $0.55$
②
모표준편차가 $2\sqrt{2}$인 정규분포를 따르는 모집단에서 크기가 $128$인 표본을 임의추출하여 얻은 표본평균의 값이 $\bar{x}$일 때, 이를 이용하여 구한 모평균 $m$에 대한 신뢰도 $95$%의 신뢰구간은
$\bar{x}-1.96\times\frac{2\sqrt{2}}{\sqrt{128}} \le m \le \bar{x}+1.96\times\frac{2\sqrt{2}}{\sqrt{128}}$이고
이 신뢰구간이 $\bar{x}-c \le m \le \bar{x}+c$이므로
$c = 1.96 \times \frac{2\sqrt{2}}{\sqrt{128}}$ $= 1.96 \times \frac{1}{4} = 0.49$
① $\frac{1}{4}$
② $\frac{5}{16}$
③ $\frac{3}{8}$
④ $\frac{7}{16}$
⑤ $\frac{1}{2}$
④
확률변수 $X$가 가질 수 있는 값은 $0$, $1$, $2$이다.
(ⅰ) $X = 0$인 경우
두 상자의 바닥에 닿은 면에 적혀있는 두 수가 서로 같아야 하므로
$\mathrm{P}(X=0)$ $= \frac{1}{4} \times \frac{1}{4} + \frac{2}{4} \times \frac{2}{4} + \frac{1}{4} \times \frac{1}{4}$
$= \frac{1}{16}+\frac{4}{16}+\frac{1}{16}$ $= \frac{6}{16}$
(ⅱ) $X=1$인 경우
두 상자의 바닥에 닿은 면에 적혀있는 두 수가 $1$, $2$ 또는 $2$, $3$이어야 하므로
$\mathrm{P}(X=1)$ $= \frac{1}{4} \times \frac{2}{4} \times 2 + \frac{2}{4} \times \frac{1}{4} \times 2$
$= \frac{4}{16}+\frac{4}{16}$ $= \frac{8}{16}$
(ⅲ) $X=2$인 경우
두 상자의 바닥에 닿은 면에 적혀있는 두 수가 $1$, $3$이어야 하므로
$\mathrm{P}(X=2)$ $= \frac{1}{4} \times \frac{1}{4} \times 2= \frac{2}{16}$
(ⅰ), (ⅱ), (ⅲ)에 의하여
$\mathrm{E}(X)$ $= 0 \times \frac{6}{16} + 1 \times \frac{8}{16} + 2 \times \frac{2}{16}$
$= \frac{12}{16} = \frac{3}{4}$,
$\mathrm{E}(X^{2})$ $= 0^{2} \times \frac{6}{16} + 1^{2} \times \frac{8}{16} + 2^{2} \times \frac{2}{16}$
$= \frac{16}{16} = 1$
이므로
$\mathrm{V}(X) = \mathrm{E}(X^{2})-(\mathrm{E}(X))^{2}$
$= 1-(\frac{3}{4})^{2} = 1-\frac{9}{16}$ $= \dfrac{7}{16}$
(가) 두 학생 $\mathrm{A}$, $\mathrm{B}$는 각각 $1$장 이상의 카드를 받고, 학생 $\mathrm{C}$는 카드를 받지 못할 수 있다.
(나) 학생 $\mathrm{A}$가 받는 카드의 색의 가짓수는 $3$ 이하이다.
① $730$
② $746$
③ $762$
④ $778$
⑤ $794$
②
빨간색 카드 $1$장을 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 나누어 주는 경우의 수
${}_{3}\mathrm{C}_{1} = 3$
파란색 카드 $1$장을 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 나누어 주는 경우의 수는 위와 마찬가지로
$3$
노란색 카드 $3$장을 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 나누어 주는 경우의 수는 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$가 받는 노란색 카드의 수를 각각 $a_{y}$, $b_{y}$, $c_{y}$라 할 때 방정식 $a_{y} + b_{y} + c_{y} += 3$을 만족시키는 음이 아닌 정수 $a_{y}$, $b_{y}$, $c_{y}$의 순서쌍 $(a_{y}, b_{y}, c_{y})$의 개수와 같으므로
${}_{3}\mathrm{H}_{3} = {}_{3+3-1}\mathrm{C}_{3}= {}_{5}\mathrm{C}_{2} = 10$
보라색 카드 $3$장을 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 나누어 주는 경우의 수는 위와 마찬가지로
$10$
따라서 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 $8$장의 카드를 남김없이 나누어 주는 경우의 수는
$3 \times 3 \times 10 \times 10 = 900$
(ⅰ) 학생 $\mathrm{A}$가 카드를 한 장도 받지 못하는 경우의 수는 모든 카드를 두 학생 $\mathrm{B}$, $\mathrm{C}$에게만 나누어 주는 경우의 수와 같으므로
${}_{2}\mathrm{C}_{1} \times {}_{2}\mathrm{C}_{1} \times {}_{2}\mathrm{H}_{3} \times {}_{2}\mathrm{H}_{3}$
$= 2^{2} \times ({}_{2+3-1}\mathrm{C}_{3})^{2}$ $= 4 \times ({}_{4}\mathrm{C}_{1})^{2} = 64$
(ⅱ) 학생 $\mathrm{B}$가 카드를 한 장도 받지 못하는 경우의 수는 (ⅰ)과 마찬가지로
$64$
(ⅲ) 두 학생 $\mathrm{A}$, $\mathrm{B}$ 모두 카드를 한 장도 받지 못하는 경우의 수는 모든 카드를 학생 $\mathrm{C}$에게만 나누어 주는 경우의 수와 같으므로
$1$
(ⅰ), (ⅱ), (ⅲ)에서 규칙 (가)에 따라 카드를 나누어 주는 경우의 수는
$900-(64+64-1)=773$
학생 $\mathrm{A}$가 서로 다른 $4$가지 색의 카드를 받고 학생 $\mathrm{B}$가 카드를 $1$장 이상 받는 경우의 수를 구해보자.
학생 $\mathrm{A}$가 빨간색 카드와 파란색 카드, 노란색 카드, 보라색 카드를 각각 $1$장씩 받으면 남는 카드는 노란색 카드 $2$장과 보라색 카드 $2$장뿐이다.
노란색 카드 $2$장과 보라색 카드 $2$장을 세 학생 $\mathrm{A}$, $\mathrm{B}$, $\mathrm{C}$에게 나누어 주는 경우의 수는
${}_{3}\mathrm{H}_{2} \times {}_{3}\mathrm{H}_{2}$ $= ({}_{3+2-1}\mathrm{C}_{2})^{2}$ $= ({}_{4}\mathrm{C}_{2})^{2} = 6^{2} = 36$
한편, 노란색 카드 $2$장과 보라색 카드 $2$장을 두 학생 $\mathrm{A}$, $\mathrm{C}$에게만 나누어 주는 경우의 수는
${}_{2}\mathrm{H}_{2} \times {}_{2}\mathrm{H}_{2}$ $= ({}_{2+2-1}\mathrm{C}_{2})^{2}$ $= ({}_{3}\mathrm{C}_{1})^{2} = 3^{2} = 9$
따라서 학생 $\mathrm{A}$가 서로 다른 $4$가지 색의 카드를 받고 학생 $\mathrm{B}$가 카드를 $1$장 이상 받는 경우의 수는
$36-9=27$
따라서 규칙 (가), (나)에 따라 카드를 나누어 주는 경우의 수는
$773-27 = 746$

29. 두 집합 $A = \{ 2, 3, 4 \}$, $B = \{ 2, 3 \}$에 대하여 다음 시행을 한다.
집합 $A$의 모든 부분집합 $8$개 중에서 임의로 한 개를 선택하고,
집합 $B$의 모든 부분집합 $4$개 중에서 임의로 한 개를 선택한다.
선택한 두 집합의 교집합의 원소의 개수를 기록한다.
이 시행을 $15360$번 반복하여 기록한 수가 $1$인 횟수가 $5880$ 이상일 확률을 오른쪽 표준정규분포표를 이용하여 구한 값이 $k$일 때, $1000 \times k$의 값을 구하시오. [4점]
$15360$번 반복하여 기록한 수가 $1$인 횟수가 $5880$ 이상일 확률을 오른쪽 표준정규분포표를 이용하여 구한 값이 $k$일 때, $1000 \times k$의 값을 구하시오. [4점]
$23$
집합 $A$의 모든 부분집합 $8$개 중에서 임의로 한 개를 선택하는 사건을 $C$, 집합 $B$의 모든 부분집합 $4$개 중에서 임의로 한 개를 선택하는 사건을 $D$라 하면 선택한 두 집합의 교집합의 원소의 개수가 $1$인 경우는 그 교집합이 $\{ 2 \}$ 또는 $\{ 3 \}$
일 때이다.
(ⅰ) 교집합이 $\{ 2 \}$일 때
① 사건 $C$에서 $\{ 2 \}$를 선택하면 사건 $D$에서 $\{ 2 \}$ 또는 $\{ 2, 3 \}$을 선택하면 된다.
② 사건 $C$에서 $\{ 2, 3 \}$을 선택하면 사건 $D$에서 $\{ 2 \}$를 선택하면 된다.
③ 사건 $C$에서 $\{ 2, 4 \}$를 선택하면 사건 $D$에서 $\{ 2 \}$ 또는 $\{ 2, 3 \}$을 선택하면 된다.
④ 사건 $C$에서 $\{ 2, 3, 4 \}$를 선택하면 사건 $D$에서 $\{ 2 \}$를 선택하면 된다.
따라서 이 경우의 확률은
$\frac{2+1+2+1}{8 \times 4} = \frac{3}{16}$
(ⅱ) 교집합이 $\{ 3 \}$일 때
① 사건 $C$에서 $\{ 3 \}$을 선택하면 사건 $D$에서 $\{ 3 \}$ 또는 $\{ 2, 3 \}$을 선택하면 된다.
② 사건 $C$에서 $\{ 2, 3 \}$을 선택하면 사건 $D$에서 $\{ 3 \}$을 선택하면 된다.
③ 사건 $C$에서 $\{ 3, 4 \}$를 선택하면 사건 $D$에서 $\{ 3 \}$ 또는 $\{ 2, 3 \}$을 선택하면 된다.
④ 사건 $C$에서 $\{ 2, 3, 4 \}$를 선택하면 사건 $D$에서 $\{ 3 \}$을 선택하면 된다.
따라서 이 경우의 확률은
$\frac{2+1+2+1}{8 \times 4} = \frac{3}{16}$
(ⅰ), (ⅱ)에 의하여 선택한 두 집합의 교집합의 원소의 개수가 $1$일 확률은
$\frac{3}{16}+\frac{3}{16} = \frac{3}{8}$
이때 기록한 수가 $1$인 횟수를 확률변수 $X$라 하면 $X$는 이항분포 $\mathrm{B}(15360, \frac{3}{8})$을 따른다.
또한 $\mathrm{E}(X) = 15360 \times \frac{3}{8} = 5760$,
$\mathrm{\sigma}(X) = \sqrt{15360 \times \frac{3}{8} \times \frac{5}{8}} = 60$이고 $15360$은 충분히 큰 수이므로 확률변수 $X$는 근사적으로 정규분포 $\mathrm{N}(5760, 60^{2})$을 따른다.
따라서 $k = \mathrm{P}(X \ge 5880)$ $= \mathrm{P}(Z \ge \frac{5880-5760}{60}) = \mathrm{P}(Z \ge 2) = 0.5-\mathrm{P}(0 \le Z \le 2)$ $= 0.5-0.477 = 0.023$
따라서 $1000 \times k = 1000 \times 0.023 = 23$
$\bullet$ 카드를 내려놓은 학생이 $2$명이면 더 큰 수가 적힌 카드를 내려놓은 학생만 귤을 받는다.
$\bullet$ 카드를 내려놓은 학생이 $1$명이면 카드를 내려놓지 않은 학생만 귤을 받는다.
$\bullet$ 카드를 내려놓은 학생이 없으면 어느 학생도 귤을 받지 못한다.
$p = q$일 때, $24(n+p)$의 값을 구하시오. (단, $n$은 $7$ 이하의 자연수이다.) [4점]
$80$
학생 $\mathrm{A}$가 카드를 내려놓을 확률은 $\frac{1}{2}$이고, 학생 $\mathrm{A}$가 카드를 내려놓게 되는 경우, 내려놓은 카드에 적힌 수는 $8$이다.
학생 $\mathrm{B}$가 카드를 내려놓을 확률은 $\frac{n-1}{6}$이고, 학생 $\mathrm{B}$가 카드를 내려놓게 되는 경우, 내려놓은 카드에 적힌 수는 $n$ 이하이고 어떤 카드를 내려놓더라도 카드에 적힌 수는 $8$ 보다 작다.
학생 $\mathrm{A}$가 카드를 내려놓는 사건을 $A$, 학생 $\mathrm{B}$가 카드를 내려놓는 사건을 $B$라 하자.
학생 $A$가 귤을 받는 경우는 두 학생 $A$, $B$가 모두 카드를 내려놓는
경우이거나, 학생 $B$만 카드를 내려놓는 경우이므로 확률 $p$는
$p = \mathrm{P}(A) \times \mathrm{P}(B) + \mathrm{P}(A^{c}) \times \mathrm{P}(B)$
$= \frac{1}{2} \times \frac{n-1}{6}+(1-\frac{1}{2}) \times \frac{n-1}{6}$ $= \frac{n-1}{6}$
학생 $B$가 귤을 받는 경우는 학생 $A$만 카드를 내려놓는 경우이므로 확률 $q$는
$q = \mathrm{P}(A) \times \mathrm{P}(B^{c})$
$= \frac{1}{2} \times (1-\frac{n-1}{6})$ $= \frac{7-n}{12}$
$p=q$에서 $\frac{n-1}{6} = \frac{7-n}{12}$
$n = 3$이고 $p = \frac{3-1}{6} = \frac{1}{3}$이므로
$24(n+p) = 24 \times (3 + \frac{1}{3}) = 80$
수학 영역(미적분)

① $e$
② $2e$
③ $3e$
④ $4e$
⑤ $5e$
① $e-2$
② $\frac{e-1}{2}$
③ $\frac{e}{2}$
④ $e-1$
⑤ $\frac{e+1}{2}$
④
$\displaystyle \int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}\cos\left( x-\frac{\pi}{4}\right)e^{\sin(x-\frac{\pi}{4})}dx$에서
$\sin(x-\frac{\pi}{4}) = t$로 놓으면
$\frac{dt}{dx} = \cos(x-\frac{\pi}{4})$이다.
이때, $x = \frac{\pi}{4}$일 때 $t=0$이고
$x = \frac{3\pi}{4}$일 때 $t=1$이므로
$\int_{\frac{\pi}{4}}^{\frac{3\pi}{4}}\cos\left( x-\frac{\pi}{4}\right)e^{\sin(x-\frac{\pi}{4})}dx$
$= \int_{0}^{1}e^{t}dt$ $= \bigg[ \: e^{t}\, \bigg]_{0}^{1} = e^{1}-e^{0} = e-1$
① $6$
② $8$
③ $10$
④ $12$
⑤ $14$
②
$\displaystyle \lim_{n \to \infty}\frac{an^{b}}{\sqrt{n^{4}+4n}-\sqrt{n^{4}+n}} = 6$에서
$\displaystyle \lim_{n \to \infty}\frac{an^{b}}{\sqrt{n^{4}+4n}-\sqrt{n^{4}+n}}$
$= \displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{(\sqrt{n^{4}+4n}-\sqrt{n^{4}+n})(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}$
$= \displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{(n^{4}+4n)-(n^{4}+n)}$
$= \displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n}$
이므로
$\displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n} = 6$ $\cdots\cdots$ ㉠
(ⅰ) $b \gt -1$일 때,
$\displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n}$의 값은 존재하지 않으므로 ㉠을 만족시키지 못한다.
(ⅱ) $b \lt -1$일 때,
$\displaystyle \lim_{n \to \infty}\frac{an^{b}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n} = 0$이므로 ㉠을 만족시키지 못한다.
(ⅲ) $b = -1$일 때,
㉠에서
$\displaystyle \lim_{n \to \infty}\frac{an^{-1}(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n}$
$= \displaystyle \lim_{n \to \infty}\frac{a(\sqrt{n^{4}+4n}+\sqrt{n^{4}+n})}{3n^{2}}$
$= \displaystyle \lim_{n \to \infty}\frac{a\left(\sqrt{1+\frac{4}{n^3}}+\sqrt{1+\frac{1}{n^3}}\right)}{3}$
$= \frac{2a}{3}$
이므로
$\frac{2a}{3} = 6$, $a = 9$
(ⅰ), (ⅱ), (ⅲ)에서 $a = 9$, $b = -1$
따라서 $a+b = 9+(-1) = 8$
① $4-3\ln3$
② $3-3\ln2$
③ $4-2\ln3$
④ $3+3\ln2$
⑤ $3+3\ln3$
①
$1 = \frac{3}{x-1}$에서 $x=4$이므로 $\mathrm{A}(4, 1)$
$3 = \frac{3}{x-1}$에서 $x=2$이므로 $\mathrm{B}(2, 3)$
직선 $\mathrm{AB}$의 방정식은
$y-1 = \frac{3-1}{2-4}(x-4)$
$y = -x+5$
따라서 구하는 도형의 넓이는
$\int_{2}^{4}(-x+5-\frac{3}{x-1})dx$
$= \bigg[ -\frac{1}{2}x^{2}+5x-3\ln |\,x-1\,|\bigg]_{2}^{4}$
$= (-8+20-3 \ln 3)-(-2+10-3 \ln 1)$
$= 4-3 \ln 3$
두 점 $\mathrm{A}$, $\mathrm{B}$에서 $x$축에 내린 수선의 발을 각각 $\mathrm{C}$, $\mathrm{D}$라 하면 사각형 $\mathrm{ABDC}$의
넓이는
$\frac{1}{2}\times (1+3)\times 2 = 4$
따라서 구하는 넓이는
$4-\int_{2}^{4}\frac{3}{x-1}dx = 4-\bigg[ 3\ln |\,x-1\,|\bigg]_{2}^{4}$
$= 4-3 \ln 3$
① $\frac{5}{4}$
② $\frac{11}{8}$
③ $\frac{3}{2}$
④ $\frac{13}{8}$
⑤ $\frac{7}{4}$
①
함수 $f(x^{3}+x)$의 역함수가 $g(x)$이므로 모든 실수 $x$에 대하여
$g(f(x^{3}+x)) = x$ $\cdots\cdots$ ㉠
가 성립한다.
$x^{3}+x = 2$에서 $x^{3}+x-2 = 0$
$(x-1)(x^{2}+x+2) = 0$ $\cdots\cdots$ ㉡
이때,
$x^{2}+x+2 = (x+\frac{1}{2})^{2}+\frac{7}{4} \gt 0$
이므로 ㉡에서 $x=1$
㉠의 양변에 $x=1$을 대입하면 $g(f(2)) = 1$이고,
$f(2) = 1$이므로 $g(1) = 1$
한편, ㉠의 양변을 $x$에 대하여 미분하면
$g'(f(x^{3}+x)) \times f'(x^{3}+x) \times (3x^{2}+1) = 1$
위 등식의 양변에 $x=1$을 대입하면
$g'(f(2)) \times f'(2) \times 4 = 1$
$f(2) = 1$이므로
$4g'(1) \times f'(2) = 1$ $\cdots\cdots$ ㉢
$f'(2) = 8g'(1)-1$을 ㉢에 대입하면
$4g'(1) \times (8g'(1)-1) = 1$, $32(g'(1))^{2}-4g'(1)-1 = 0$
$(4g'(1)-1)(8g'(1)+1) = 0$
$g'(1) = \frac{1}{4}$ 또는 $g'(1) = -\frac{1}{8}$
(ⅰ) $g'(1) = \frac{1}{4}$일 때,
$f'(2) = 8g'(1)-1 = 8\times \frac{1}{4}-1 = 1 \gt 0$
이므로 모든 실수 $x$에 대하여 $f'(x) \gt 0$이라는 조건을 만족시킨다.
(ⅱ) $g'(1) = -\frac{1}{8}$일 때,
$f'(2) = 8g'(1)-1 = 8\times (-\frac{1}{8})-1 = -2 \lt 0$
이므로 모든 실수 $x$에 대하여 $f'(x) \gt 0$이라는 조건을 만족시키지 못한다.
(ⅰ), (ⅱ)에서 $g'(1) = \frac{1}{4}$이므로
$g(1)+g'(1) = 1+\frac{1}{4} = \frac{5}{4}$
(가) $f(0) = 0$, $f''(\pi) = 0$
(나) $\sin g(\pi) = 0$, $\displaystyle \lim_{x \to \infty}g(x) = \frac{3\pi}{2}$
① $-12$
② $-6$
③ $-1$
④ $3$
⑤ $9$
②
$\sin g(\pi) = 0$에서 $g(\pi) = n\pi$인 정수 $n$이 존재한다.
$f'(x) = g'(x)-\sec^{2}g(x) \times g'(x)$
$= g'(x) (1-\sec^{2}g(x))$ $= -g'(x) \tan^{2}g(x)$
의 양변에 $x=\pi$를 대입하면
$f'(\pi) = -g'(\pi) \tan^{2}g(\pi) = 0$
조건 (가)에서 $f^{”}(\pi) = 0$이므로
$f(x) = a(x-\pi)^{3}+b$ ($a$, $b$는 상수, $a \ne 0$) 이고
$f(0) = -a\pi^{3}+b = 0$이므로 $b = a\pi^{3}$
$f(x) = a(x-\pi)^{3}+a\pi^{3}$
그러므로 $f(\pi) = a\pi^{3}$이고 $f(\pi) = g(\pi)-\tan g(\pi) = n\pi$이므로
$a\pi^{3} = n\pi$에서 $a = \frac{n}{\pi^{2}}$
이때 모든 실수 $x$에 대하여 $\tan g(x)$가 정의되기 위해서는 모든 실수 $x$에 대하여 $g(x) = k\pi + \frac{\pi}{2}$ ($k$는 정수)이어야 한다. $\cdots\cdots$ ㉠
또 $f'(x) = 3a(x-\pi)^{2}$이므로
$3a(x-\pi)^{2} = -g'(x) \tan^{2}g(x)$ $\cdots\cdots$ ㉡
(ⅰ) $a \gt 0$인 경우
$x$가 $\pi$가 아닐 때 $g'(x) \lt 0$이므로 $g(x)$는 감소하고 $n \gt 0$이다.
$x \gt \pi$일 때, $g(\pi) = n\pi$에서 $g(x)$는 $\frac{3}{2}\pi$로 감소한다.
$n\pi \gt \frac{3}{2}\pi$이므로 $n \gt \frac{3}{2}$
이때 $g(x)$의 치역은 $(\frac{3}{2}\pi, \,n\pi \,]$이므로 ㉠에 의해서
$n\pi \lt \frac{5}{2}\pi$, $n \lt \frac{5}{2}$
즉, $\frac{3}{2} \lt n \lt \frac{5}{2}$이므로 $n = 2$
(ⅱ) $a \lt 0$인 경우
$x$가 $\pi$가 아닐 때 $g'(x) \gt 0$이므로 $g(x)$는 증가하고 $n \lt 0$이다.
$g(\pi) = n\pi$에서 $g(x)$는 $\frac{3}{2}\pi$로 증가하는데 ㉠에 의하여 모순이다.
(ⅰ), (ⅱ)에서 $n = 2$이므로 $a = \frac{2}{\pi^{2}}$
$f(0) = g(0)-\tan g(0) = 0$에서
$f'(0) = -g'(0) \tan^{2}g(0) = -g'(0)(g(0))^{2}$
따라서 $g'(0)(g(0))^{2} = -f'(0)$ $= -3a\pi^{2} = -3 \times \frac{2}{\pi^{2}} \times \pi^{2} = -6$

$\displaystyle \sum_{n=1}^{\infty}a_n = \frac{q}{p}$일 때, $p+q$의 값을 구하시오. (단, $p$와 $q$는 서로소인 자연수이다.) [4점]
$91$
등비수열 $\{ a_n \}$의 첫째항이 양수이므로 $a_1 \gt 0$이다.
등비수열 $\{ a_n \}$의 공비를 $r$ (단, $r$은 유리수)라 하면 급수 $\displaystyle \sum_{n=1}^{\infty}a_n$이 수렴하므로 $-1 \lt r \lt 1$이다.
조건 (나)에서 수열 $\{ a_n \}$의 정수인 항의 개수는 $3$이고 공비가 $-1 \lt r \lt 1$이므로 정수인 세 항은 연속해서 나와야 한다.
즉, 세 항 $a_{m}$, $a_{m+1}$, $a_{m+2}$의 값이 모두 정수인 자연수 $m$이 존재하고,
이때, $|\,a_{m}\,| \gt |\,a_{m+1}\,| \gt |\,a_{m+2}\,|$이다.
$0$이 아닌 실수 $x$에 대하여
$a_{m} = x$, $a_{m+1} = xr$, $a_{m+2} = xr^{2}$이라 하면
조건 (나)에 의해
$a_{m}\times a_{m+1}\times a_{m+2} = 216$ $\cdots\cdots$ ㉠
이므로
$x\times xr\times xr^{2} = 216$이다.
즉, $(xr)^{3} = 216 = 6^{3}$이고, $xr$이 실수이므로 $xr = 6$
㉠에서 $a_{m+1} = xr = 6$이므로
$a_{m}\times 6 \times a_{m+2} = 216$
$a_{m}\times a_{m+2} = 36$
이때, $a_{m}$, $a_{m+2}$가 모두 정수이므로
$|\,a_{m}\,| = 36$, $|\,a_{m+2}\,| = 1$ 또는 $|\,a_{m}\,| = 18$, $|\,a_{m+2}\,| = 2$ 또는 $|\,a_{m}\,| = 12$, $|\,a_{m+2}\,| = 3$ 또는 $|\,a_{m}\,| = 9$, $|\,a_{m+2}\,| = 4$
(ⅰ) $|\,a_{m}\,| = 9$, $|\,a_{m+2}\,| = 4$일 때,
$a_{m+1} = 6$이므로
$\dfrac{|\,a_{m+1}\,|}{|\,a_{m}\,|} = \dfrac{|\,a_{m+2}\,|}{|\,a_{m+1}\,|} = \dfrac{2}{3}$
즉, $|\,r\,| = \frac{2}{3}$ 이므로
$r = \frac{2}{3}$ 또는 $r = -\frac{2}{3}$
① $r = \frac{2}{3}$일 때,
$a_{m} = 9$, $a_{m+1} = 6$, $a_{m+2} = 4$이므로 $a_1$의 최솟값은 $9$이다.
이때 $a_2 = 6$이므로
$a_{1} + a_{2} = 9 + 16 = 15 \gt 10$이다.
즉, 조건 (가)를 만족시키지 못한다.
② $r = -\frac{2}{3}$일 때,
$a_{m} = -9$, $a_{m+1} = 6$, $a_{m+2} = -4$이고, $a_1 \gt 0$이므로
$a_{2} = -9$일 때 $a_{1}$의 값은 최소이다.
이때 $a_{1} = a_{2} \times (-\frac{3}{2}) = -9 \times (-\frac{3}{2}) = \frac{27}{2}$ 이고,
$a_{1} + a_{2} = \frac{27}{2}+(-9) = \frac{9}{2} \lt 10$
이므로 조건 (가)를 만족시킨다.
(ⅱ) $|\,a_{m}\,| \gt 9$일 때,
$-1 \lt r \lt 1$이고 $a_1 \gt 0$이므로 (ⅰ)과 같은 방법으로 계산해 보면
$a_{1} + a_{2} \ge 10$임을 알 수 있다.
즉, 조건 (가)를 만족시키지 못한다.
(ⅰ), (ⅱ)에서 $a_{1} = \frac{27}{2}$, $r = -\frac{2}{3}$이므로
$\displaystyle \sum_{n=1}^{\infty}a_{n} = \dfrac{\frac{27}{2}}{1-(-\frac{2}{3})} = \dfrac{81}{10}$
따라서 $p = 10$, $q = 81$이므로
$p+q = 10 + 81 = 91$
등비수열 $\{ a_n \}$의 첫째항이 양수이므로 $a_1 \gt 0$
등비수열 $\{ a_n \}$의 공비를 $r$ (단, $r$은 유리수)라 하면 급수 $\displaystyle \sum_{n=1}^{\infty}a_{n}$이 수렴하므로 $-1 \lt r \lt 1$이다.
조건 (나)에서 수열 $\{ a_n \}$의 정수인 항의 개수는 $3$이고 이 세 항의 곱이 $216$이므로 수열 $\{ a_n \}$의 정수인 세 항의 값을 $x$, $y$, $z$ ($|\,x\,| \gt |\,y\,| \gt |\,z\,|$)라 하면 $xyz = 216$이다.
이때, $216 = 2^{3} \times 3^{3}$이고 $|\,x\,| \times |\,y\,| \times |\,z\,| = 216$이므로 $|\,x\,|$의 값의 최솟값은 $9$이다.
(ⅰ) $|\,x\,| = 9$일 때,
$|\,y\,| = 6$, $|\,z\,| = 4$
두 수 $|\,x\,|$, $|\,y\,|$가 등비수열 $\{ a_n \}$의 서로 다른 두 항이므로
$\dfrac{|\,y\,|}{|\,x\,|} = |\,r\,|^{m}$을 만족시키는 자연수 $m$이 존재한다.
$\frac{|\,y\,|}{|\,x\,|} = \frac{6}{9} = \frac{2}{3}$이므로
$|\,r\,|^{m} = \frac{2}{3}$이고,
공비 $r$이 유리수이어야 하므로
$m = 1$, $|\,r\,| = \frac{2}{3}$이다.
이때, $\frac{|\,z\,|}{|\,y\,|} = \frac{4}{6} = \frac{2}{3}$이므로 세 수 $x$, $y$, $z$는 등비수열 $\{ a_n \}$의 연속된 세 항의 값이다.
한편 $|\,r\,| = \frac{2}{3}$에서 $r = \frac{2}{3}$ 또는 $r = -\frac{2}{3}$
① $r = \frac{2}{3}$일 때,
$a_1$의 최솟값은 $9$이고 이때 $a_{2} = 6$이므로
$a_{1} + a_{2} = 9+6 = 15 \gt 10$이다.
즉, 조건 (가)를 만족시키지 못한다.
② $r = -\frac{2}{3}$일 때,
$xyz = 216$이고 세 수 $x$, $y$, $z$는 등비수열 $\{ a_n \}$의 연속된 세 항의 값이므로 $x \lt 0$, $y \gt 0$, $z \lt 0$이어야 한다.
즉, $x = -9$, $y = 6$, $z = -4$
이때, $a_1 \gt 0$이므로 $2$보다 큰 자연수 $k$에 대하여 $a_{k} = 9$이면 $a_{1}+a_2 \gt 10$이다.
즉, 조건 (가)를 만족시키지 못한다.
$a_{2} = -9$일 때, $a_{1} = a_{2} \times (-\frac{3}{2}) = -9 \times (-\frac{3}{2})$ $= \frac{27}{2}$이므로
$a_{1} + a_{2} = \frac{27}{2} + (-9) = \frac{9}{2} \lt 10$이다.
즉, 조건 (가)를 만족시킨다.
(ⅱ) $|\,x\,| \gt 9$일 때,
$-1 \lt r \lt 1$이고 $a_1 \gt 0$이므로 (ⅰ)과 같은 방법으로 하면 $a_{1} + a_{2} \ge 10$이므로 조건 (가)를 만족시키지 못한다.
(ⅰ), (ⅱ)에서 $a_{1} = \frac{27}{2}$, $r = -\frac{2}{3}$이므로
$\displaystyle \sum_{n=1}^{\infty}a_{n} = \dfrac{\frac{27}{2}}{1-(-\frac{2}{3})} = \dfrac{81}{10}$
따라서 $p = 10$, $q = 81$이므로
$p+q = 10 + 81 = 91$
$31$
$f(1) = 4\ln 2 = \ln 16$에서 $e^{f(1)} = 16$
또 $f(x) = \ln \left( \frac{g(x)}{1+xf'(x)} \right)$에서
$e^{f(x)} = \frac{g(x)}{1+xf'(x)}$
$g(x) = e^{f(x)} + xf'(x)e^{f(x)}$이고
$\int_{1}^{2}g(x)dx$ $= \int_{1}^{2}e^{f(x)}dx + \int_{1}^{2}xf'(x)e^{f(x)} dx$
$= \int_{1}^{2}e^{f(x)}dx + \bigg[ xe^{f(x)}\bigg]_{1}^{2}-\int_{1}^{2}e^{f(x)} dx$
$= 2e^{f(2)}-e^{f(1)}$ $= 2e^{f(2)}-16 = 34$
이므로
$e^{f(2)} = 25$
따라서
$\int_{1}^{2}xg(x)dx$ $= \int_{1}^{2}xe^{f(x)}dx + \int_{1}^{2}x^{2}f'(x)e^{f(x)} dx$
$= \int_{1}^{2}xe^{f(x)}dx + \bigg[ x^{2}e^{f(x)}\bigg]_{1}^{2}-\int_{1}^{2}2xe^{f(x)} dx$
$= 4e^{f(2)}-e^{f(1)}-\int_{1}^{2}xe^{f(x)} dx$ $= 100-16-\int_{1}^{2}xe^{f(x)} dx = 53$
에서
$\displaystyle \int_{1}^{2}xe^{f(x)} dx = 84-53 = 31$
수학 영역(기하)

① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
① $1$
② $2$
③ $3$
④ $4$
⑤ $5$
① $10$
② $12$
③ $14$
④ $16$
⑤ $18$
① $\sqrt{21}$
② $\sqrt{22}$
③ $\sqrt{23}$
④ $2\sqrt{6}$
⑤ $5$
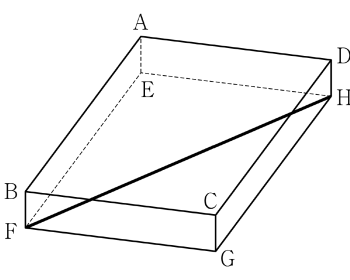
①
점 $\mathrm{A}$에서 평면 $\mathrm{EFGH}$에 내린 수선의 발이 점 $\mathrm{E}$이고, 점 $\mathrm{E}$에서 선분 $\mathrm{FH}$에 내린 수선의 발을 $\mathrm{I}$라 하면 삼수선의 정리에 의하여 두 선분 $\mathrm{AI}$와 $\mathrm{FH}$는 서로 수직이다.
그러므로 점 $\mathrm{A}$와 직선 $\mathrm{FH}$ 사이의 거리는 선분 $\mathrm{AI}$의 길이와 같다.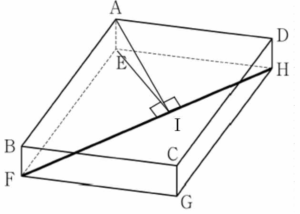 직각삼각형 $\mathrm{EFH}$에서 $\overline{\mathrm{EF}} = 10$, $\overline{\mathrm{EH}} = 5$이므로 피타고라스 정리에 의하여
직각삼각형 $\mathrm{EFH}$에서 $\overline{\mathrm{EF}} = 10$, $\overline{\mathrm{EH}} = 5$이므로 피타고라스 정리에 의하여
$\overline{\mathrm{FH}}^{2} = \overline{\mathrm{EF}}^{2} + \overline{\mathrm{EH}}^{2}$
$= 10^{2} + 5^{2} = 125$
$\overline{\mathrm{FH}} = 5\sqrt{5}$
직각삼각형 $\mathrm{EFH}$의 넓이를 구하는 식에서
$\frac{1}{2} \times \overline{\mathrm{EF}} \times \overline{\mathrm{EH}} = \frac{1}{2} \times \overline{\mathrm{FH}} \times \overline{\mathrm{EI}}$
$\frac{1}{2} \times 10 \times 5 = \frac{1}{2} \times 5\sqrt{5} \times \overline{\mathrm{EI}}$
$\overline{\mathrm{EI}} = 2\sqrt{5}$
직각삼각형 $\mathrm{AEI}$에서 피타고라스 정리에 의하여
$\overline{\mathrm{AI}}^{2} = \overline{\mathrm{AE}}^{2} + \overline{\mathrm{EI}}^{2}$
$= 1^{2} + (2\sqrt{5})^{2} = 21$
$\overline{\mathrm{AI}} = \sqrt{21}$
따라서 점 $\mathrm{A}$와 직선 $\mathrm{FH}$ 사이의 거리는 $\overline{\mathrm{AI}} = \sqrt{21}$
① $-\frac{7\sqrt{3}}{9}$
② $-\frac{2\sqrt{3}}{3}$
③ $-\frac{5\sqrt{3}}{9}$
④ $-\frac{4\sqrt{3}}{9}$
⑤ $-\frac{\sqrt{3}}{3}$
②
쌍곡선의 방정식이 $\frac{x^{2}}{9}-\frac{y^2}{16} = -1$이므로
$c^{2} = 9 + 16 = 25$
즉, 두 초점의 좌표는 $\mathrm{F}(0, 5)$, $\mathrm{F’}(0, -5)$
점 $\mathrm{P}$가 제$\,2\,$사분면에 있으므로
$\overline{\mathrm{PF}} \lt \overline{\mathrm{PF’}}$
쌍곡선의 정의에 의하여
$\overline{\mathrm{PF’}}-\overline{\mathrm{PF}} = 8$ $\cdots\cdots$ ㉠
삼각형 $\mathrm{PF’F}$의 둘레의 길이가 $30$이고 $\overline{\mathrm{FF’}} = 10$이므로
$\overline{\mathrm{PF’}}+\overline{\mathrm{PF}} = 20$ $\cdots\cdots$ ㉡
㉠, ㉡에서 $\overline{\mathrm{PF}} = 6$, $\overline{\mathrm{PF’}} = 14$
점 $\mathrm{P}$의 좌표를 $(a, b)$라 하면
$\overline{\mathrm{PF}}^{2} = a^{2}+(b-5)^{2} = 36$ $\cdots\cdots$ ㉢
$\overline{\mathrm{PF’}}^{2} = a^{2}+(b+5)^{2} = 196$ $\cdots\cdots$ ㉣
㉢, ㉣에서 $a \lt 0$, $b \gt 0$이므로 $a = -3\sqrt{3}$, $b = 8$
즉, $\mathrm{P}(-3\sqrt{3}, 8)$이므로 주어진 쌍곡선 위의 점 $\mathrm{P}$에서의 접선의 방정식은
$\frac{-3\sqrt{3}x}{9}-\frac{8y}{16}= -1$
$y = -\frac{2\sqrt{3}}{3}x+2$
따라서 구하는 접선의 기울기는 $-\dfrac{2\sqrt{3}}{3}$
(가) 선분 $\mathrm{OA}$ 위의 $\overline{\mathrm{OC}} = 4$인 점 $\mathrm{C}$에 대하여 직선 $\mathrm{BC}$와 $xy$평면이 서로 평행하다.
(나) 두 직선 $\mathrm{OA}$, $\mathrm{AB}$와 $xy$평면이 이루는 예각의 크기를 각각 $\alpha$, $\beta$라 하면 $\sin \alpha = 3 \sin \beta$이다.
① $\frac{\sqrt{2}}{6}$
② $\frac{\sqrt{2}}{5}$
③ $\frac{\sqrt{2}}{4}$
④ $\frac{\sqrt{2}}{3}$
⑤ $\frac{\sqrt{2}}{2}$
④
구 $S : x^{2}+y^{2}+z^{2} = 36$은 중심이 원점이고 반지름의 길이가 $6$인 구이다.
두 점 $\mathrm{A}$, $\mathrm{B}$가 모두 구 $S$ 위의 점이므로
$\overline{\mathrm{OA}} = \overline{\mathrm{OB}} = 6$
두 점 $\mathrm{A}$, $\mathrm{B}$에서 $xy$평면에 내린 수선의 발을 각각 $\mathrm{A’}$, $\mathrm{B’}$이라 하자.
조건 (가)에서 점 $\mathrm{C}$가 선분 $\mathrm{OA}$ 위의 점이므로 점 $\mathrm{C}$에서 직선 $\mathrm{AA’}$에 내린 수선의 발은 선분 $\mathrm{AA’}$ 위에 있다.
이 수선의 발을 $\mathrm{H}$라 하자.
이때 직선 $\mathrm{BC}$와 $xy$평면이 서로 평행하므로 두 점 $\mathrm{B}$, $\mathrm{C}$의 $z$좌표가 서로 같고, 점 $\mathrm{B}$에서 선분 $\mathrm{AA’}$에 내린 수선의 발도 점 $\mathrm{H}$이다.
두 직선 $\mathrm{OA}$, $\mathrm{AB}$와 $xy$평면이 이루는 예각의 크기가 각각 $\alpha$, $\beta$이고 두 평면 $\mathrm{BHC}$, $xy$평면이 서로 평행하므로
$\angle \mathrm{ACH} = \alpha$, $\angle \mathrm{ABH} = \beta$
두 직각삼각형 $\mathrm{ACH}$, $\mathrm{ABH}$에서
$\sin \alpha = \frac{\overline{\mathrm{AH}}}{\overline{\mathrm{AC}}}$, $\sin \beta = \frac{\overline{\mathrm{AH}}}{\overline{\mathrm{AB}}}$
이고 조건 (나)에서 $\sin \alpha = 3 \sin \beta$이므로
$\frac{\overline{\mathrm{AH}}}{\overline{\mathrm{AC}}} = 3 \times \frac{\overline{\mathrm{AH}}}{\overline{\mathrm{AB}}}$, 즉 $\overline{\mathrm{AB}} = 3\overline{\mathrm{AC}}$
$\overline{\mathrm{AC}} = \overline{\mathrm{OA}}-\overline{\mathrm{OC}} = 6-4 = 2$이므로
$\overline{\mathrm{AB}} = 3\overline{\mathrm{AC}} = 3 \times 2 = 6$
그러므로 삼각형 $\mathrm{OAB}$는 한 변의 길이가 $6$인 정삼각형이다.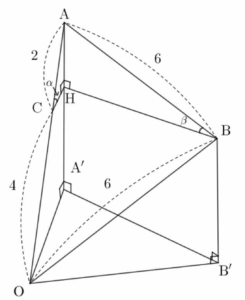 $\overline{\mathrm{AH}} = h$라 하면 두 직선 $\mathrm{CH}$, $\mathrm{OA’}$이 서로 평행하므로
$\overline{\mathrm{AH}} = h$라 하면 두 직선 $\mathrm{CH}$, $\mathrm{OA’}$이 서로 평행하므로
$\overline{\mathrm{AH}} : \overline{\mathrm{HA’}} = \overline{\mathrm{AC}} : \overline{\mathrm{CO}}$
$h : \overline{\mathrm{HA’}} = 2 : 4$
$\overline{\mathrm{HA’}} = 2h$
직각삼각형 $\mathrm{AOA^{′}}$에서 피타고라스 정리에 의하여
$\overline{\mathrm{OA^{′}}}^{2}+\overline{\mathrm{AA^{′}}}^{2}=\overline{\mathrm{OA}}^{2}$
$\overline{\mathrm{OA^{′}}}^{2}+(3h)^{2} = 6^{2}$
$\overline{\mathrm{OA^{′}}} = \sqrt{36-9h^{2}}$ $\cdots\cdots$ ㉠
직각삼각형 $\mathrm{OB^{′}B}$에서 피타고라스 정리에 의하여
$\overline{\mathrm{OB^{′}}}^{2}+\overline{\mathrm{B^{′}B}}^{2}=\overline{\mathrm{OB}}^{2}$
$\overline{\mathrm{OB^{′}}}^{2}+\overline{\mathrm{A^{′}H}}^{2}=\overline{\mathrm{OB}}^{2}$
$\overline{\mathrm{OB^{′}}}^{2}+(2h)^{2} = 6^{2}$
$\overline{\mathrm{OB^{′}}} = \sqrt{36-4h^{2}}$ $\cdots\cdots$ ㉡
직각삼각형 $\mathrm{AHB}$에서 피타고라스 정리에 의하여
$\overline{\mathrm{AH}}^{2}+\overline{\mathrm{HB}}^{2}=\overline{\mathrm{AB}}^{2}$
$h^{2}+\overline{\mathrm{HB}}^{2} = 6^{2}$
$\overline{\mathrm{HB}} = \sqrt{36-h^{2}}$
$\overline{\mathrm{A^{‘}B^{‘}}} = \overline{\mathrm{HB}}$이므로
$\overline{\mathrm{A^{‘}B^{‘}}} = \sqrt{36-h^{2}}$ $\cdots\cdots$ ㉢
조건에서 삼각형 $\mathrm{OAB}$의 $xy$평면 위로의 정사영인 삼각형 $\mathrm{OA′B′}$이 직각삼각형이다.
이때 ㉠, ㉡, ㉢에서 $\overline{\mathrm{A^{‘}B^{‘}}} \gt \overline{\mathrm{OB^{‘}}} \gt \overline{\mathrm{OA^{‘}}}$이므로 직각삼각형 $\mathrm{OA^{‘}B^{‘}}$의 빗변의 길이는 $\overline{\mathrm{A^{‘}B^{‘}}}$이고 밑변과 높이의 길이는 $\overline{\mathrm{OB^{‘}}}$, $\overline{\mathrm{OA^{‘}}}$이다.
직각삼각형 $\mathrm{OA^{‘}B^{‘}}$에서 피타고라스 정리에 의하여
$\overline{\mathrm{A^{‘}B^{‘}}}^{2}=\overline{\mathrm{OB^{‘}}}^{2}+\overline{\mathrm{OA^{‘}}}^{2}$
$36-h^{2} = (36-4h^{2})+(36-9h^{2})$
$h^{2} = 3$, $h = \sqrt{3}$
삼각형 $\mathrm{OAB}$는 한 변의 길이가 $6$인 정삼각형이므로 삼각형 $\mathrm{OAB}$의 넓이를 $S$라 하면
$S = \frac{\sqrt{3}}{4}\times 6^{2} = 9\sqrt{3}$
삼각형 $\mathrm{OA’B’}$은 밑변과 높이의 길이가
$\overline{\mathrm{OA’}} = \sqrt{36-9h^2} = 3$, $\overline{\mathrm{OB’}} = \sqrt{36-4h^2} = 2\sqrt{6}$인 직각삼각형이므로 삼각형 $\mathrm{OA’B’}$의 넓이를 $S’$라 하면
$S’ = \frac{1}{2}\times 3 \times 2\sqrt{6} = 3\sqrt{6}$
따라서 평면 $\mathrm{OAB}$와 $xy$평면이 이루는 예각의 크기 $\theta$에 대하여 $S \cos \theta = S’$이므로
$\cos \theta = \frac{S’}{S} = \frac{3\sqrt{6}}{9\sqrt{3}}$ $= \dfrac{\sqrt{2}}{3}$

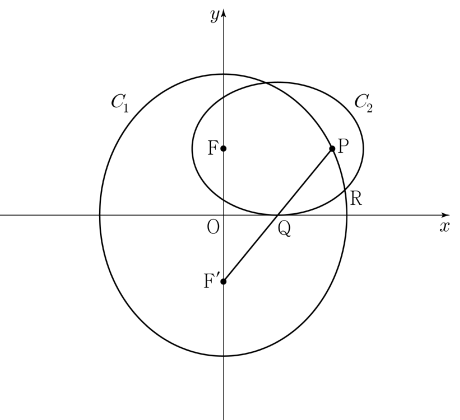
$396$
두 초점이 $\mathrm{P}$, $\mathrm{F}$인 타원 $C_2$의 꼭짓점 중 하나가 점 $\mathrm{Q}$이므로 $\overline{\mathrm{QP}} = \overline{\mathrm{QF}}$이고 점 $\mathrm{Q}$에서 선분 $\mathrm{PF}$에 내린 수선의 발을 $\mathrm{M}$이라 하면 $\overline{\mathrm{MP}} = \overline{\mathrm{MF}}$이다.
두 직선 $\mathrm{FF’}$, $\mathrm{MQ}$가 서로 평행하므로 두 삼각형 $\mathrm{PMQ}$, $\mathrm{PFF’}$은 닮음비가 $\overline{\mathrm{PM}} : \overline{\mathrm{PF}} = 1 : 2$인 닮은 삼각형이다.
이때 $\overline{\mathrm{MQ}} = \frac{1}{2}\overline{\mathrm{FF’}}$ $= \frac{1}{2}\times 12 = 6$이다.
$\overline{\mathrm{MP}} = a$, $\overline{\mathrm{PQ}} = b$라 하자. 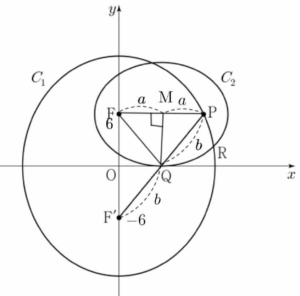 직각삼각형 $\mathrm{PMQ}$에서 피타고라스의 정리에 의하여
직각삼각형 $\mathrm{PMQ}$에서 피타고라스의 정리에 의하여
$\overline{\mathrm{PQ}}^{2} = \overline{\mathrm{MP}}^{2} + \overline{\mathrm{MQ}}^{2}$
$b^{2} = a^{2}+6^{2}$ $\cdots\cdots$ ㉠
두 점 $\mathrm{R}$, $\mathrm{P}$가 두 초점이 $\mathrm{F}$, $\mathrm{F’}$인 타원 $C_1$ 위에 있으므로 타원의 정의에 의하여
$\overline{\mathrm{FR}}+\overline{\mathrm{F’R}} = \overline{\mathrm{FP}}+\overline{\mathrm{F’P}}$
$\overline{\mathrm{FR}}+\overline{\mathrm{F’R}} = 2a+2b$ $\cdots\cdots$ ㉡
두 점 $\mathrm{R}$, $\mathrm{Q}$가 두 초점이 $\mathrm{F}$, $\mathrm{P}$인 타원 $C_2$ 위에 있으므로 타원의 정의에 의하여
$\overline{\mathrm{FR}}+\overline{\mathrm{PR}} = \overline{\mathrm{FQ}}+\overline{\mathrm{PQ}}$
$\overline{\mathrm{FR}}+\overline{\mathrm{PR}} = 2b$ $\cdots\cdots$ ㉢
㉡$\,-\,$㉢에서 $\overline{\mathrm{F’R}}-\overline{\mathrm{PR}} = 2a$
조건에서 $\overline{\mathrm{F’R}}-\overline{\mathrm{PR}} = 7\sqrt{2}$이므로 $2a = 7\sqrt{2}$
$a = \frac{7\sqrt{2}}{2}$
㉠에서 $b^{2}= (\frac{7\sqrt{2}}{2})^{2}+6^{2} = \frac{49}{2}+36 = \frac{121}{2}$
$b = \frac{11}{\sqrt{2}} = \frac{11\sqrt{2}}{2}$
㉡에서 타원 $C_1$의 장축의 길이는
$2a+2b = 7\sqrt{2}+11\sqrt{2} = 18\sqrt{2}$
㉢에서 타원 $C_2$의 장축의 길이는
$2b = 11\sqrt{2}$
따라서 두 타원 $C_1$, $C_2$의 장축의 길이의 곱은
$18\sqrt{2}\times 11\sqrt{2} = 396$
30. 좌표평면에 $\overline{\mathrm{AB}} = \overline{\mathrm{AC}} = 8\sqrt{5}$, $\overline{\mathrm{BC}} = 16$인 삼각형 $\mathrm{ABC}$가 있다. 선분 $\mathrm{AB}$ 위의 점 $\mathrm{P}$, 선분 $\mathrm{BC}$ 위의 점 $\mathrm{Q}$, 선분 $\mathrm{CA}$ 위의 점 $\mathrm{R}$이 다음 조건을 만족시킨다.
$69$
조건 (가)에서 $(\overrightarrow{\mathrm{PB}}+\overrightarrow{\mathrm{PQ}})\cdot\overrightarrow{\mathrm{BC}} = 0$이므로 선분 $\mathrm{BQ}$의 중점을 $\mathrm{D}$라 하면
$2\overrightarrow{\mathrm{PD}}\cdot\overrightarrow{\mathrm{BC}} = 0$
즉, $\overrightarrow{\mathrm{PD}} \perp \overrightarrow{\mathrm{BC}}$이므로 삼각형 $\mathrm{PBQ}$는 $\overline{\mathrm{PB}} = \overline{\mathrm{PQ}}$인 이등변삼각형이고 $\overline{\mathrm{PQ}} \diagup\diagup \overline{\mathrm{AC}}$
또, $(\overrightarrow{\mathrm{RC}}+\overrightarrow{\mathrm{RQ}})\cdot\overrightarrow{\mathrm{BC}} = 0$이므로 선분 $\mathrm{QC}$의 중점을 $\mathrm{E}$라 하면
$2\overrightarrow{\mathrm{RE}}\cdot\overrightarrow{\mathrm{BC}} = 0$
즉, $\overrightarrow{\mathrm{RE}} \perp \overrightarrow{\mathrm{BC}}$이므로 삼각형 $\mathrm{RQC}$는 $\overline{\mathrm{RQ}} = \overline{\mathrm{RC}}$인 이등변삼각형이고
$\overline{\mathrm{RQ}} \diagup\diagup \overline{\mathrm{AB}}$
조건 (나)에서 $\overrightarrow{\mathrm{QP}}\cdot\overrightarrow{\mathrm{QR}} = |\,\overrightarrow{\mathrm{QP}}\,|^{2}$이므로
$\angle \mathrm{PQR} = \theta$라 하면
$|\,\overrightarrow{\mathrm{QR}}\,| \cos \theta = |\,\overrightarrow{\mathrm{QP}}\,|$에서
$\cos \theta = \frac{|\,\overrightarrow{\mathrm{QP}}\,|}{|\,\overrightarrow{\mathrm{QR}}\,|}$
이를 만족시키려면 $\angle \mathrm{RPQ} = \frac{\pi}{2}$이어야 하므로 주어진 상황을 그림으로 나타내면 다음과 같다.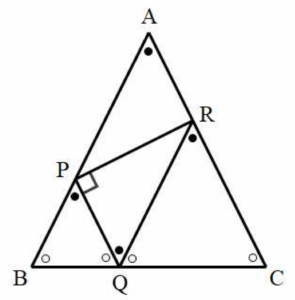 한편 삼각형 $\mathrm{ABC}$에서 코사인법칙에 의하여
한편 삼각형 $\mathrm{ABC}$에서 코사인법칙에 의하여
$\cos A = \frac{(8\sqrt{5})^{2}+(8\sqrt{5})^{2}-16^{2}}{2 \times 8\sqrt{5} \times 8\sqrt{5}}$ $= \frac{3}{5}$이고,
$\angle \mathrm{PQR} = \angle \mathrm{A}$이므로
$\frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{RQ}}} = \frac{3}{5}$
이때 두 삼각형 $\mathrm{PBQ}$, $\mathrm{RQC}$는 서로 닮음이므로
$\frac{\overline{\mathrm{BQ}}}{\overline{\mathrm{QC}}} = \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{RC}}} = \frac{\overline{\mathrm{PQ}}}{\overline{\mathrm{RQ}}} = \frac{3}{5}$이고,
$\overline{\mathrm{BQ}}+\overline{\mathrm{QC}} = 16$이므로
$\overline{\mathrm{BQ}} = 6$, $\overline{\mathrm{QC}} = 10$
그러므로 $\overline{\mathrm{PQ}} = 3\sqrt{5}$, $\overline{\mathrm{RQ}} = 5\sqrt{5}$, $\overline{\mathrm{PR}} = 4\sqrt{5}$
한편, 선분 $\mathrm{PR}$을 $1 : 3$으로 내분하는 점을 $\mathrm{S}$라 하면
$\overrightarrow{\mathrm{XS}} = \dfrac{\overrightarrow{\mathrm{XR}}+3\overrightarrow{\mathrm{XP}}}{1+3}$이므로
$3\overrightarrow{\mathrm{XP}}+\overrightarrow{\mathrm{XR}} = 4\overrightarrow{\mathrm{XS}}$이다.
즉, $|\,3\overrightarrow{\mathrm{XP}}+\overrightarrow{\mathrm{XR}}\,| = |\,\overrightarrow{\mathrm{PR}}\,|$을 만족시키는 점 $\mathrm{X}$는
$|\,\overrightarrow{\mathrm{XS}}\,| = \frac{1}{4}|\,\overrightarrow{\mathrm{PR}}\,|$을 만족시킨다.
그러므로 점 $\mathrm{X}$는 다음 그림과 같이 선분 $\mathrm{PR}$을 $1 : 3$으로 내분하는 점 $\mathrm{S}$를 중심으로 하고 점 $\mathrm{P}$를 지나는 원 위를 움직인다. 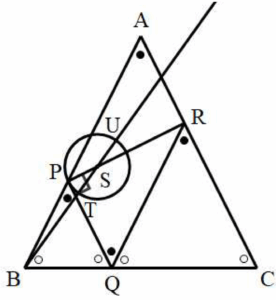 위 그림과 같이 직선 $\mathrm{BS}$가 원과 만나는 점 중 $\mathrm{B}$와 가까운 점을 $\mathrm{T}$, 먼 점을 $\mathrm{U}$라 하면
위 그림과 같이 직선 $\mathrm{BS}$가 원과 만나는 점 중 $\mathrm{B}$와 가까운 점을 $\mathrm{T}$, 먼 점을 $\mathrm{U}$라 하면
$|\,\overrightarrow{\mathrm{BT}}\,| \le |\,\overrightarrow{\mathrm{BX}}\,| \le |\,\overrightarrow{\mathrm{BU}}\,|$이므로
$M = |\,\overrightarrow{\mathrm{BU}}\,|$, $m = |\,\overrightarrow{\mathrm{BT}}\,|$이다.
한편, 삼각형 $\mathrm{PBS}$에서
$\overline{\mathrm{PB}} = \overline{\mathrm{PQ}} = 3\sqrt{5}$,
$\overline{\mathrm{PS}} = \frac{1}{4}\overline{\mathrm{PR}} = \frac{1}{4}\times 4\sqrt{5} = \sqrt{5}$,
$\angle \mathrm{SPB} = \frac{\pi}{2} + \angle \mathrm{BPQ}$ $ = \frac{\pi}{2} + \angle \mathrm{A}$
이므로 코사인법칙에 의하여
$\overline{\mathrm{BS}}^{2}$ $= \overline{\mathrm{PB}}^{2}+\overline{\mathrm{PS}}^{2}-2\times \overline{\mathrm{PB}} \times \overline{\mathrm{PS}} \times \cos (\frac{\pi}{2} + \angle \mathrm{A})$
$= 45+5+30 \times \sin (\angle \mathrm{A})$
$= 50 + 30 \times \frac{4}{5} = 74$
따라서 $M = \sqrt{74} + \sqrt{5}$, $m = \sqrt{74}-\sqrt{5}$이므로
$M \times m = (\sqrt{74} + \sqrt{5})(\sqrt{74}-\sqrt{5})$ $= 74-5 = 69$
